
第二章机电一体化机械系统设计理论 第一节概述 机电一体化机械系统是由计算机信息网络协调与控制的,用于完成包括机械力、运动和能 流等动力学任务的机械及机电部件相互联系的系统。其核心是由计算机控制的,包括机械、电力、 电子、液压、光学等技术的同服系统。它的主要功能是完成一系列机械运动,每一个机械运动可 单独由控制电动机、传动机构和执行机构组成的子系统来完成,而这些子系统要由计算机协调和 控制,以完成其系统功能要求。机电一体化机械系统的设计要从系统的角度进行合理化和最优化 设计。 机电一体化系统的机械结构主要包括执行机构、传动机构和支承部件。在机械系统设计时 除考虑一般机械设计要求外,还必须考虑机械结构因素与整个同服系统的性能参数、电气参数的 匹配,以获得良好的同服性能。 一、机电一体化对机械系统的基本要求 机电一体化系统的机械系统与一般的机械系统相比,除要求较高的制造精度外,还应具有良 好的动态响应特性,即快速响应和良好的稳定性。 1、高精度 精度直接影响产品的质量,尤其是机电一体化产品,其技术性能、工艺水平和功能比普通的 机械产品都有很大的提高,因此机电一体化机械系统的高精度是其首要的要求。如果机械系统的 精度不能满足要求,则无论机电一体化产品其它系统工作再精确,也无法完成其预定的机械操作。 2、快速响应 机电一体化系统的快速响应即是要求机械系统从接到指令到开始执行指令指定的任务之间 的时间间隔短。这样系统才能精确地完成预定的任务要求,且控制系统也才能及时根据机械系统 的运行情况得到信息,下达指令,使其准确地完成任务。 3、良好的稳定性 机电一体化系统要求其机械装置在温度、振动等外界干扰的作用下依然能够正常稳定的工 作。既系统抵御外界环境的影响和抗干扰能力强。 为确保机械系统的上述特性,在设计中通常提出无间隙、低摩擦、低惯量、高刚度、高谐振 频率和适当的阻尼比等要求。此外机械系统还要求具有体积小、重量轻、高可靠性和寿命长等特 点。 二、机械系统的组成 概括地讲,机电一体化机械系统应主要包括如下三大部分机构。 1、传动机构 机电一体化机械系统中的传动机构不仅仅是转速和转矩的变换器,而是已成为同服系统的 部分,它要根据伺服控制的要求进行选择设计,以满足整个机械系统良好的同服性能。因此传动 机构除了要满足传动精疲的要求,而且还要满足小型、轻量、高速、低噪声和高可靠性的要求。 2、导向机构 导向机构的作用是支承和导向,为机械系统中各运动装置能安全、准确地完成其特定方向的 运动提供保障,一般指导轨、轴承等。 3、执行机构
1 第二章 机电一体化机械系统设计理论 第一节 概 述 机电一体化机械系统是由计算机信息网络协调与控制的,用于完成包括机械力、运动和能量 流等动力学任务的机械及机电部件相互联系的系统。其核心是由计算机控制的,包括机械、电力、 电子、液压、光学等技术的伺服系统。它的主要功能是完成一系列机械运动,每一个机械运动可 单独由控制电动机、传动机构和执行机构组成的子系统来完成,而这些子系统要由计算机协调和 控制,以完成其系统功能要求。机电一体化机械系统的设计要从系统的角度进行合理化和最优化 设计。 机电一体化系统的机械结构主要包括执行机构、传动机构和支承部件。在机械系统设计时, 除考虑一般机械设计要求外,还必须考虑机械结构因素与整个伺服系统的性能参数、电气参数的 匹配,以获得良好的伺服性能。 一、机电一体化对机械系统的基本要求 机电一体化系统的机械系统与一般的机械系统相比,除要求较高的制造精度外,还应具有良 好的动态响应特性,即快速响应和良好的稳定性。 1、高精度 精度直接影响产品的质量,尤其是机电一体化产品,其技术性能、工艺水平和功能比普通的 机械产品都有很大的提高,因此机电—体化机械系统的高精度是其首要的要求。如果机械系统的 精度不能满足要求,则无论机电—体化产品其它系统工作再精确,也无法完成其预定的机械操作。 2、快速响应 机电一体化系统的快速响应即是要求机械系统从接到指令到开始执行指令指定的任务之间 的时间间隔短。这样系统才能精确地完成预定的任务要求,且控制系统也才能及时根据机械系统 的运行情况得到信息,下达指令,使其准确地完成任务。 3、良好的稳定性 机电一体化系统要求其机械装置在温度、振动等外界干扰的作用下依然能够正常稳定的工 作。既系统抵御外界环境的影响和抗干扰能力强。 为确保机械系统的上述特性,在设计中通常提出无间隙、低摩擦、低惯量、高刚度、高谐振 频率和适当的阻尼比等要求。此外机械系统还要求具有体积小、重量轻、高可靠性和寿命长等特 点。 二、机械系统的组成 概括地讲,机电一体化机械系统应主要包括如下三大部分机构。 1、传动机构 机电一体化机械系统中的传动机构不仅仅是转速和转矩的变换器,而是已成为伺服系统的一 部分,它要根据伺服控制的要求进行选择设计,以满足整个机械系统良好的伺服性能。因此传动 机构除了要满足传动精度的要求,而且还要满足小型、轻量、高速、低噪声和高可靠性的要求。 2、导向机构 导向机构的作用是支承和导向,为机械系统中各运动装置能安全、准确地完成其特定方向的 运动提供保障,一般指导轨、轴承等。 3、执行机构

执行机构是用以完成操作任务的直接装置。执行机构根据操作指令的要求在动力源的带动 下,完成预定的操作。一般要求它具有较高的灵敏度、精确度,良好的重复性和可靠性。由于计 算机的强大功能,使传统的作为动力源的电动机发展为具有动力、变速与执行等多重功能的同服 电动机,从而大大地简化了传动和快行机构。 除以上三部分外,机电一体化系统的机械部分通常还包括机座、支架、壳体等。 三、机城系统的设计思想 机电一体化的机械系统设计主要包括两个环节:静态设计和动态设计 1、静态设计 静态设计是指依据系统的功能要求,通过研究制定出机械系统的初步设计方案。该方案只是 个初步的轮,包括系统主要零、部件的种类,各部件之间的联接方式,系统的控制方式,所 需能源方式等。 有了初步设计方案后,开始着手按技术要求设计系统的各组成部件的结构、运动关系及参数: 零件的材料、结构、制造精度确定:执行元件(如电机)的参数、功率及过载能力的验算:相关 元、部件的选择:系统的阻尼配置等。以上称为稳态设计。稳态设计保证了系统的静态特性要求。 2、动态设计 动态设计是研究系统在频率域的特性,是借助静态设计的系统结物,通过建立系统组成各环 节的数学模型和推导出系统整体的传递函数,利用自动控制理论的方法求得该系统的频率特性(幅 频特性和相频特性)。系统的频率特性体现了系统对不同频率信号的反应,决定了系统的稳定性、 最大工作频率和坑干扰能力。 静态设计是忽路了系统自身运动因素和干扰因素的影响状态下进行的产品设计,对于伺服精 度和响应速度要求不高的电一体化系统,静态设计就能够满足设计要求。对于精密和高速智能 化机电一体化系统,环境干扰和系统自身的结构及运动因素对系统产生的影响会很大,因此必须 通过调节各个环节的相关参数,改变系统的动态特性以保证系统的功能要求。动态分析与设计过 程往往会改变前期的部分设计方案,有时甚至会推翻整个方案,要求重新进行静态设计。 第二节机械传动设计的原则 一种把动力机产生的运动和动力传递给执行机构的中间装置,是一种扭矩和转速 的变换器,其目的是在动力机与负载之间使扭矩得到合理的匹配,并可通过机构变换实现对输出 的速度调节。 在机电一体化系统中,伺服电动机的同服变速功能在很大程度上代替了传统机械传动中的变 速机构,只有当伺服电机的转速范围满足不了系统要求时,才通过传动装置变速。由于机电一体 化系统对快速响应指标要求很高,因此机电一体化系统中的机械传动装置不仅仅是解决同服电机 与负载间的力矩匹配问题。而更重要的是为了提高系统的同服性能。为了提高机械系统的伺服州 能,要求机械传动部件转动惯量小、摩擦小、阻尼合理、刚度大、抗振性好、间隙小,并满足小 型、轻量、高球、低噪声和高可靠性等要求, 二、总传动比的确定 根据上面所述,机电一体化系统的传动装置在满足同服电机与负载的力矩匹配的同时,应具 有较高的响应速度,即启动和制动速度。因此,在伺服系统中,通常采用负载角加速度最大原则 2
2 执行机构是用以完成操作任务的直接装置。执行机构根据操作指令的要求在动力源的带动 下,完成预定的操作。一般要求它具有较高的灵敏度、精确度,良好的重复性和可靠性。由于计 算机的强大功能,使传统的作为动力源的电动机发展为具有动力、变速与执行等多重功能的伺服 电动机,从而大大地简化了传动和执行机构。 除以上三部分外,机电一体化系统的机械部分通常还包括机座、支架、壳体等。 三、机械系统的设计思想 机电一体化的机械系统设计主要包括两个环节:静态设计和动态设计。 1、静态设计 静态设计是指依据系统的功能要求,通过研究制定出机械系统的初步设计方案。该方案只是 一个初步的轮廓,包括系统主要零、部件的种类,各部件之间的联接方式,系统的控制方式,所 需能源方式等。 有了初步设计方案后,开始着手按技术要求设计系统的各组成部件的结构、运动关系及参数; 零件的材料、结构、制造精度确定;执行元件(如电机)的参数、功率及过载能力的验算;相关 元、部件的选择;系统的阻尼配置等。以上称为稳态设计。稳态设计保证了系统的静态特性要求。 2、动态设计 动态设计是研究系统在频率域的特性,是借助静态设计的系统结构,通过建立系统组成各环 节的数学模型和推导出系统整体的传递函数,利用自动控制理论的方法求得该系统的频率特性(幅 频特性和相频特性)。系统的频率特性体现了系统对不同频率信号的反应,决定了系统的稳定性、 最大工作频率和抗干扰能力。 静态设计是忽略了系统自身运动因素和干扰因素的影响状态下进行的产品设计,对于伺服精 度和响应速度要求不高的机电一体化系统,静态设计就能够满足设计要求。对于精密和高速智能 化机电一体化系统,环境干扰和系统自身的结构及运动因素对系统产生的影响会很大,因此必须 通过调节各个环节的相关参数,改变系统的动态特性以保证系统的功能要求。动态分析与设计过 程往往会改变前期的部分设计方案,有时甚至会推翻整个方案,要求重新进行静态设计。 第二节 机械传动设计的原则 一、机电一体化系统对机械传动的要求 机械传动是一种把动力机产生的运动和动力传递给执行机构的中间装置,是一种扭矩和转速 的变换器,其目的是在动力机与负载之间使扭矩得到合理的匹配,并可通过机构变换实现对输出 的速度调节。 在机电一体化系统中,伺服电动机的伺服变速功能在很大程度上代替了传统机械传动中的变 速机构,只有当伺服电机的转速范围满足不了系统要求时,才通过传动装置变速。由于机电一体 化系统对快速响应指标要求很高,因此机电一体化系统中的机械传动装置不仅仅是解决伺服电机 与负载间的力矩匹配问题。而更重要的是为了提高系统的伺服性能。为了提高机械系统的伺服性 能,要求机械传动部件转动惯量小、摩擦小、阻尼合理、刚度大、抗振性好、间隙小,并满足小 型、轻量、高速、低噪声和高可靠性等要求。 二、总传动比的确定 根据上面所述,机电一体化系统的传动装置在满足伺服电机与负载的力矩匹配的同时,应具 有较高的响应速度,即启动和制动速度。因此,在伺服系统中,通常采用负载角加速度最大原则

选择总传动此,以提高同服系统的响应速 度。传动模型如图21所示。 图中Jm一一电动机M转子的转动惯量 On一一电动机M的角位移 JL——负载L的转动惯量 7777777Ju T一一摩擦阻转矩 -齿轮系G的总传动此 图2-1电机、传动装置和负载的传动模型 根据传动关系有 (2-1) 0.o.o 式中日。、日m、日。一一电动机的角位移、角速度、角加速度: 9、8、 一一负载的角位移、角速度、角加速度。 T换算到电动机轴上的阻抗转矩为T/:九换算到电动机轴上的转动惯量为/P。设 Tm为电动机的驱动转矩,在忽略传动装置惯量的前提下,根据旋转运动方程,电动机轴上的合转 矩Ta为 工=7.-4=.+为s.-(.+片)x, 则8L=(Ti-Te)J2+J,) (2-2) 上式中收变总传动批则日,也随之改变。根据负载角加速度大的原则,令4日=0, 侧解得: 若不计摩擦,即T=0 i=√J/Jm或T/2=T (2-3) 上式表明,传动装置总传动比ⅰ的最佳值就是上换算到电动机轴上的转动惯量正好等于电动 机转子的转动惯量J,此时,电动机的输出转矩一半用于加速负载,一半用于加速电动机转子, 达到了惯性负载和转矩的最佳匹配。 当然,上述分析是忽略了传动装置的惯量影响而得到的结论,实际总传动比要依据传动装置 的惯量估算适当择大一点。在传动装置设计完以后,在动态设计时,通常将传动装置的转动 量归算为负载折算到电机轴上,并与实际负载一同考虑进行电机响应速度验算。 三、传动链的级数和各级传动比的分配 3
3 选择总传动比,以提高伺服系统的响应速 度。传动模型如图 2-1 所示。 图中 Jm——电动机 M 转子的转动惯量 m ——电动机M 的角位移 JL——负载L 的转动惯量 TLF——摩擦阻转矩 i ——齿轮系G 的总传动比 根据传动关系有 •• •• • • = = = L m L m L m i (2-1) 式中 m 、 m • 、 m •• 一一电动机的角位移、角速度、角加速度; L 、 L • 、 L •• ——负载的角位移、角速度、角加速度。 TLF换算到电动机轴上的阻抗转矩为 TLF / i; JL换算到电动机轴上的转动惯量为JL / i 2。 设 Tm为电动机的驱动转矩,在忽略传动装置惯量的前提下,根据旋转运动方程,电动机轴上的合转 矩 Ta为 L L m m L m LF a m i i J J i J J i T T T •• •• = + = − = + 2 2 则 ( )/( ) 2 m LF m L L = T i −T J i + J •• (2-2) 上式中改变总传动比 i,则 L •• 也随之改变。根据负载角加速度最大的原则,令 = 0 •• di d L , 则解得: m L m LF m LF J J T T T T i + = + 2 若不计摩擦,即 TLF=0 则 i = J L Jm i = Tm 2 L / 或T / (2-3) 上式表明,传动装置总传动比 i的最佳值就是JL换算到电动机轴上的转动惯量正好等于电动 机转子的转动惯量Jm,此时,电动机的输出转矩一半用于加速负载,—半用于加速电动机转子, 达到了惯性负载和转矩的最佳匹配。 当然,上述分析是忽略了传动装置的惯量影响而得到的结论,实际总传动比要依据传动装置 的惯量估算适当选择大一点。在传动装置设计完以后,在动态设计时,通常将传动装置的转动惯 量归算为负载折算到电机轴上,并与实际负载一同考虑进行电机响应速度验算。 三、传动链的级数和各级传动比的分配 图 2-1 电机、传动装置和负载的传动模型

机电一体化传动系统中,为既满足总传动比要求,又使结构紧凑,常采用多级齿轮副或蜗轮 蜗杆等其它传动机枸组成传动链。下面以齿轮传动链为例,介绍级数和各级传动比的分配原则, 这些原则对其它形式的传动链也有指导意义。 1、等效转动惯量最小原则 齿轮系传递的功率不同,其传动此的分配也有所不同。 (1)小功率传动装置 电动机驱动的二级齿轮传动系统如图22所示。由于功率小,假定各主动轮具有相同的转动 惯量1:轴与轴承转动惯量不计:各齿轮均为实心圆柱齿轮,且齿宽b和材料均相同:效率不计 则有 4=2x (24) 42=2-1672g 式中、。一齿轮系中第一、第二级 齿轮副的传动此: 一一齿轮系总传动此,i=iin。 同理,对于n级齿轮系 =2品7 图2-2电动机驱动的两级齿轮传动 (2-5 i= 2 (2-6 由此可见,各级传动比分配的结果应遵循“前小后大”的原则。 例2-1设=80,传动级数=4的小功率传动,试按等效转动惯量最小原则分配传动比。 4=2×80=1.7268 4=V2(品)尝=21085 13=2(”)卢=3.1438 i4=√2(婴)=6.9887 验算I=iiii≈80 以上是已知传动级数进行各级传动比的确定。若以传动级数为参变量,齿轮系中折算到电动 机轴上的等效转动惯量J。与第一级主动齿轮的转动惯量J1之比为J小,其变化与总传动此i的关 系如图23所示
4 机电一体化传动系统中,为既满足总传动比要求,又使结构紧凑,常采用多级齿轮副或蜗轮 蜗杆等其它传动机构组成传动链。下面以齿轮传动链为例,介绍级数和各级传动比的分配原则, 这些原则对其它形式的传动链也有指导意义。 1、等效转动惯量最小原则 齿轮系传递的功率不同,其传动比的分配也有所不同。 (1)小功率传动装置 电动机驱动的二级齿轮传动系统如图 2-2所示.。由于功率小,假定各主动轮具有相同的转动 惯量J1;轴与轴承转动惯量不计;各齿轮均为实心圆柱齿轮,且齿宽 b和材料均相同;效率不计。 则有 ( ) 1/ 3 i 1 = 2 i (2-4) 1/ 6 2 / 3 i 2 2 i − = 式中 i1、i2 ——齿轮系中第一、第二级 齿轮副的传动比; i——齿轮系总传动比, i = i1i2。 同理,对于n 级齿轮系 2 1 1 1 2 2 1 2 2 2 − − − − = n n n n i i ( ) (2-5) ( ) 2 1 1 2 2 2 2 − − = n k n i k i (2-6) 由此可见,各级传动比分配的结果应遵循“前小后大”的原则。 例 2-1 设 i=80,传动级数n = 4 的小功率传动,试按等效转动惯量最小原则分配传动比。 解 ( ) 2( ) 6.9887 2 3.1438 2( ) 2.1085 2 80 1.7268 1 5 8 2 1 5 4 4 / 2 2 4 2 ( 2 1) 2 4 / 2 1 4 2 1 1) 4 2( 2 4 1 4 2 2 80 4 2 80 3 2 80 2 1 = = = = = = = = − − − − − − i i i i 验算 I=i1i2i3i4≈80 以上是已知传动级数进行各级传动比的确定。若以传动级数为参变量,齿轮系中折算到电动 机轴上的等效转动惯量 Je与第一级主动齿轮的转动惯量 J1之比为 Je/J1,其变化与总传动比 i 的关 系如图 2-3 所示。 图 2-2 电动机驱动的两级齿轮传动
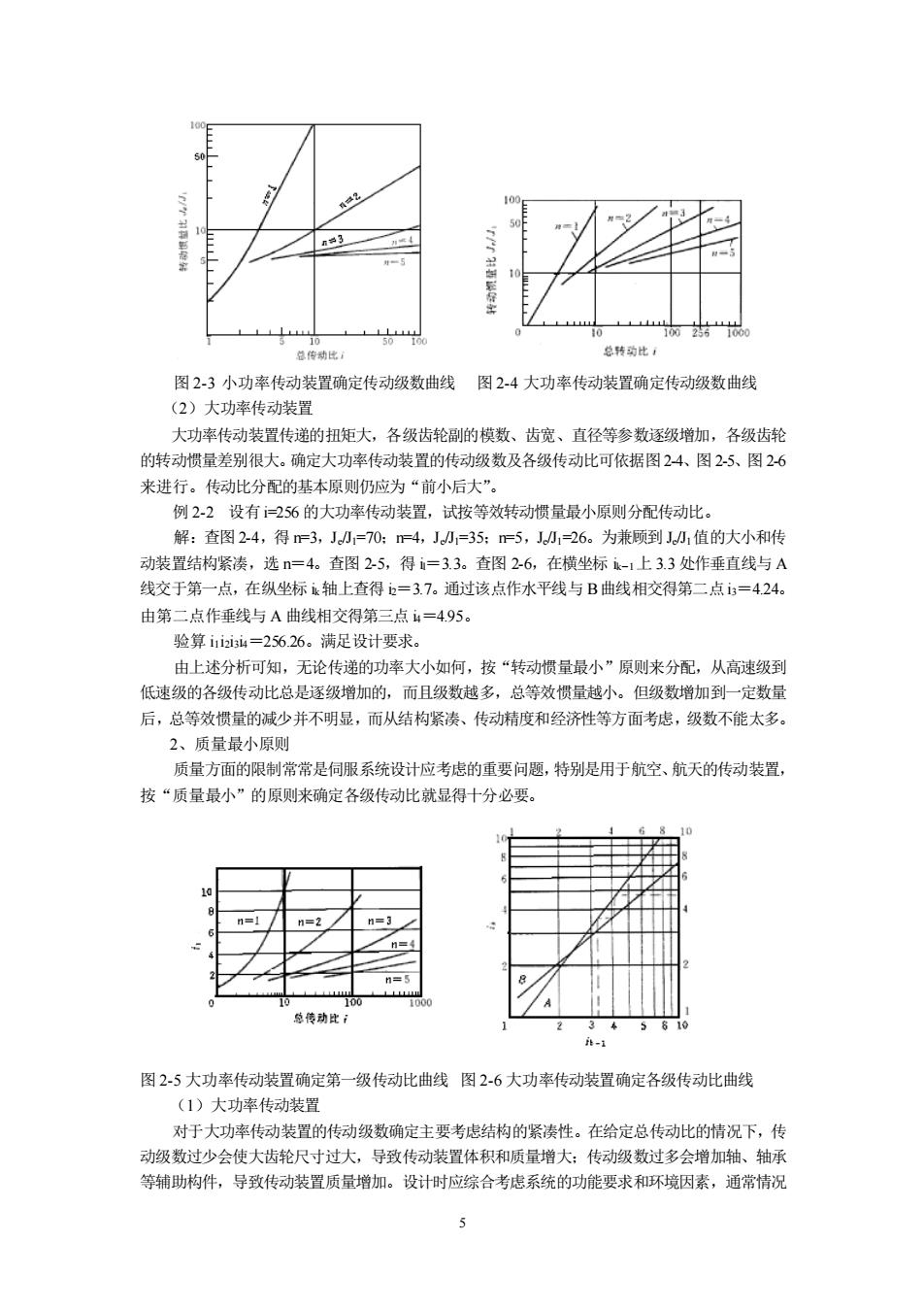
3 总传比 图23小功率传动装置确定传动级数曲线 图2-4大功率传动装置确定传动级数曲线 (2)大功率传动装置 大功率传动装置传递的扭矩大,各级齿轮副的模数、齿宽、直径等参数逐级增加,各级齿轮 的转动惯量差别很大。确定大功率传动装置的传动级数及各级传动比可依据图24、图25、图26 来进行。传动比分配的基本原则仍应为“前小后大”。 例2-2设有=256的大功率传动装置,试按等效转动惯量最小原则分配传动此。 解:查图24,得=3,J小=70:4,J小=35:=5,小1=26。为兼顾到值的大小和传 动装置结构紧凑,选n=4。查图2-5,得i=3.3。查图26,在横坐标1-1上3.3处作垂直线与A 线交于第一点,在纵坐标1轴上查得=3.7。通过该点作水平线与B曲线相交得第二点3=424. 由第二点作垂线与A曲线相交得第三点4=495。 验算iii=25626。满足设计要求。 由上述分析可知,无论传递的功率大小如何,按“转动惯量最小”原则来分配,从高速级到 低速级的各级传动比总是逐级增加的,而且级数越多,总等效惯量越小。但级数增加到一定数量 后,总等效惯量的减少并不明显,而从结构紧凑、传动情疲和经济性等方面考虑,级数不能太多。 2、质量最小原则 质量方面的限制常常是伺服系统设计应考虑的重要问题,特别是用于航空、航天的传动装置, 按“质量最小”的原则来确定各级传动比就显得十分必要。 h- 图2-5大功率传动装置确定第一级传动比曲线图2-6大功率传动装置确定各级传动此曲线 (1)大功率传动装置 对于大功率传动装置的传动级数确定主要考虑结构的紧凑性。在给定总传动此的情况下,传 动级数过少会使大齿轮尺寸过大,导致传动装置体积和质量增大:传动级数过多会增加轴、轴示 等辅助构件,导致传动装置质量增加。设计时应综合考虑系统的功能要求和环境因素,通常情况
5 图 2-3 小功率传动装置确定传动级数曲线 图 2-4 大功率传动装置确定传动级数曲线 (2)大功率传动装置 大功率传动装置传递的扭矩大,各级齿轮副的模数、齿宽、直径等参数逐级增加,各级齿轮 的转动惯量差别很大。确定大功率传动装置的传动级数及各级传动比可依据图 2-4、图 2-5、图 2-6 来进行。传动比分配的基本原则仍应为“前小后大”。 例 2-2 设有i=256 的大功率传动装置,试按等效转动惯量最小原则分配传动比。 解:查图 2-4,得 n=3,Je/J1=70;n=4,Je/J1=35;n=5,Je/J1=26。为兼顾到 Je/J1值的大小和传 动装置结构紧凑,选 n=4。查图 2-5,得 il=3.3。查图 2-6,在横坐标 ik-1上 3.3 处作垂直线与 A 线交于第一点,在纵坐标 ik轴上查得 i2=3.7。通过该点作水平线与 B曲线相交得第二点i3=4.24。 由第二点作垂线与 A 曲线相交得第三点 i4=4.95。 验算 i1i2i3i4=256.26。满足设计要求。 由上述分析可知,无论传递的功率大小如何,按“转动惯量最小”原则来分配,从高速级到 低速级的各级传动比总是逐级增加的,而且级数越多,总等效惯量越小。但级数增加到一定数量 后,总等效惯量的减少并不明显,而从结构紧凑、传动精度和经济性等方面考虑,级数不能太多。 2、质量最小原则 质量方面的限制常常是伺服系统设计应考虑的重要问题,特别是用于航空、航天的传动装置, 按“质量最小”的原则来确定各级传动比就显得十分必要。 图 2-5 大功率传动装置确定第一级传动比曲线 图 2-6 大功率传动装置确定各级传动比曲线 (1)大功率传动装置 对于大功率传动装置的传动级数确定主要考虑结构的紧凑性。在给定总传动比的情况下,传 动级数过少会使大齿轮尺寸过大,导致传动装置体积和质量增大;传动级数过多会增加轴、轴承 等辅助构件,导致传动装置质量增加。设计时应综合考虑系统的功能要求和环境因素,通常情况
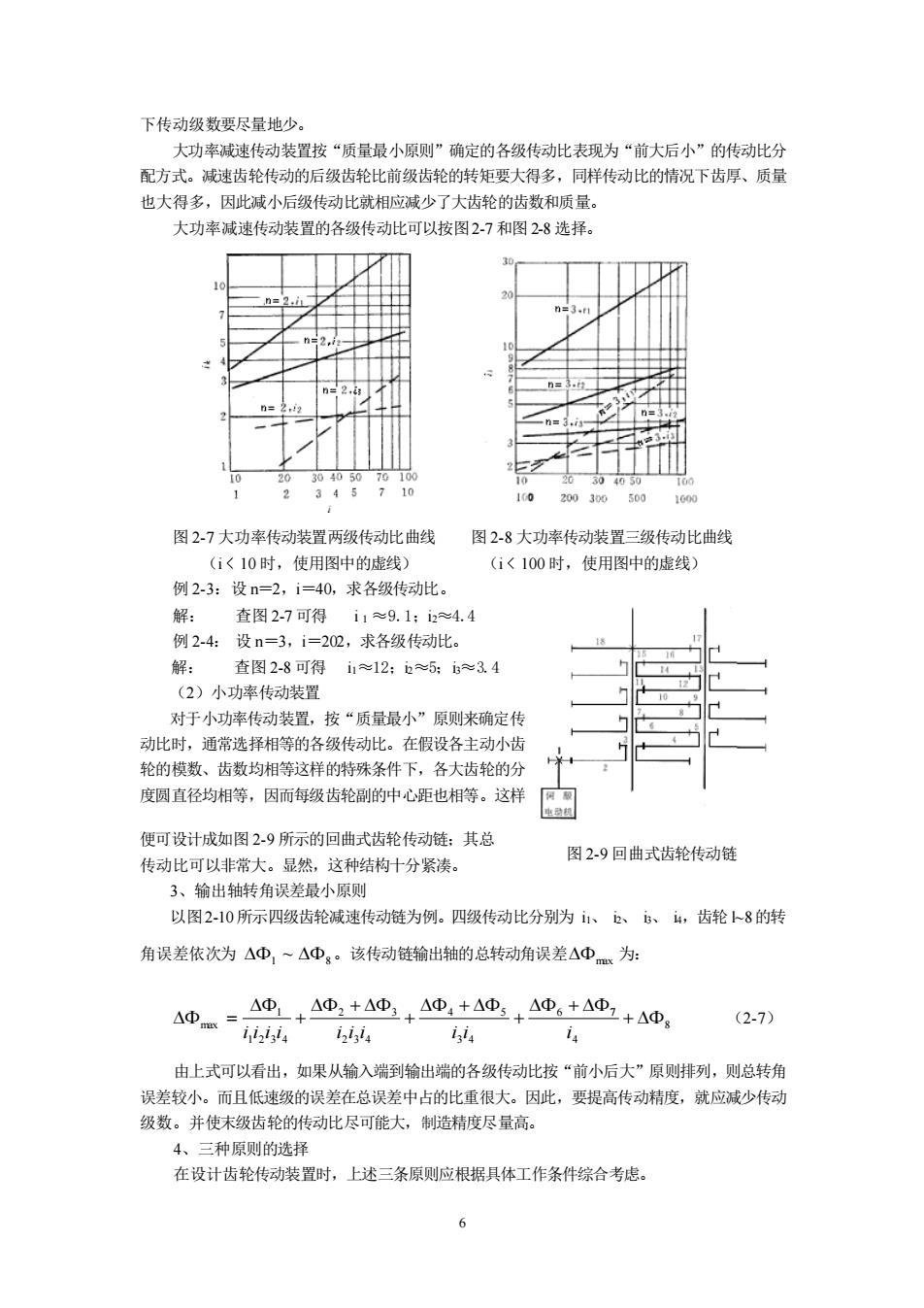
下传动级数要尽量地少。 大功率减速传动装置按“质量最小原则”确定的各级传动表现为“前大后小”的传动比分 配方式。减速齿轮传动的后级齿轮比前级齿轮的转矩要大得多,同样传动比的情祝下齿厚、质量 也大得多,因此减小后级传动比就相应减少了大齿轮的齿数和质量。 大功率诚速传动装置的各级传动此可以按图2-7和图28选择。 10 200300 00 图27大功率传动装置两级传动比曲线 图2.8大功率传动装置三级传动比曲线 (1<10时,使用图中的虚线 (i<100时,使用图中的虚线) 例2-3:设n=2,i=40,求各级传动此。 解 查图2-7可得i1≈9.1:2≈4.4 例2-4:设n=3,i=22,求各级传动此。 解: 查图28可得i1≈12:b≈5:i3≈3.4 (2)小功率传动装置 对于小功率传动装置,按“质量最小”原则来确定传 动此时,通常选择相等的各级传动此。在假设各主动小齿 轮的模数、齿数均相等这样的特殊条件下,各大齿轮的分 度圆直径均相等,因而每级齿轮副的中心距也相等。这样 便可设计成如图2-9所示的回曲式齿轮传动链:其总 图2-9回曲式齿轮传动链 传动比可以非常大。显然,这种结构十分紧凑 3、输出轴转角误差最小原划 以图2-10所示四级齿轮减速传动链为例。四级传动比分别为、。、、4,齿轮上8的转 角误差依次为△心,一△Dg。该传动链输出轴的总转动角误差△中为: △+△,+A+A,+A+A9+A1+A A中m=iig4 (2-7) 24 由上式可以看出,如果从输入端到输出端的各级传动比按“前小后大”原则排列,则总转角 误差较小。而且低速级的误差在总误差中占的比重很大。因此,要提高传动精度,就应减少传动 级数。并使末级齿轮的传动此尽可能大,制造精度尽量高。 4、三种原则的选择 在设计齿轮传动装置时,上述三条原则应根据具体工作条件综合考虑。 6
6 下传动级数要尽量地少。 大功率减速传动装置按“质量最小原则”确定的各级传动比表现为“前大后小”的传动比分 配方式。减速齿轮传动的后级齿轮比前级齿轮的转矩要大得多,同样传动比的情况下齿厚、质量 也大得多,因此减小后级传动比就相应减少了大齿轮的齿数和质量。 大功率减速传动装置的各级传动比可以按图2-7 和图 2-8 选择。 图 2-7 大功率传动装置两级传动比曲线 图 2-8 大功率传动装置三级传动比曲线 (i < 10 时,使用图中的虚线) (i < 100 时,使用图中的虚线) 例 2-3:设 n=2,i=40,求各级传动比。 解: 查图 2-7 可得 i 1 ≈9.1;i2≈4.4 例 2-4: 设 n=3,i=202,求各级传动比。 解: 查图 2-8 可得 i1≈12;i2≈5;i3≈3.4 (2)小功率传动装置 对于小功率传动装置,按“质量最小”原则来确定传 动比时,通常选择相等的各级传动比。在假设各主动小齿 轮的模数、齿数均相等这样的特殊条件下,各大齿轮的分 度圆直径均相等,因而每级齿轮副的中心距也相等。这样 便可设计成如图 2-9 所示的回曲式齿轮传动链;其总 传动比可以非常大。显然,这种结构十分紧凑。 3、输出轴转角误差最小原则 以图2-10所示四级齿轮减速传动链为例。四级传动比分别为 i1、 i2、 i3、 i4,齿轮 l~8的转 角误差依次为 1 ~ 8 。该传动链输出轴的总转动角误差 max 为: 8 4 6 7 3 4 4 5 2 3 4 2 3 1 2 3 4 1 max + + + + + + + = i i i i i i i i i i (2-7) 由上式可以看出,如果从输入端到输出端的各级传动比按“前小后大”原则排列,则总转角 误差较小。而且低速级的误差在总误差中占的比重很大。因此,要提高传动精度,就应减少传动 级数。并使末级齿轮的传动比尽可能大,制造精度尽量高。 4、三种原则的选择 在设计齿轮传动装置时,上述三条原则应根据具体工作条件综合考虑。 图 2-9 回曲式齿轮传动链
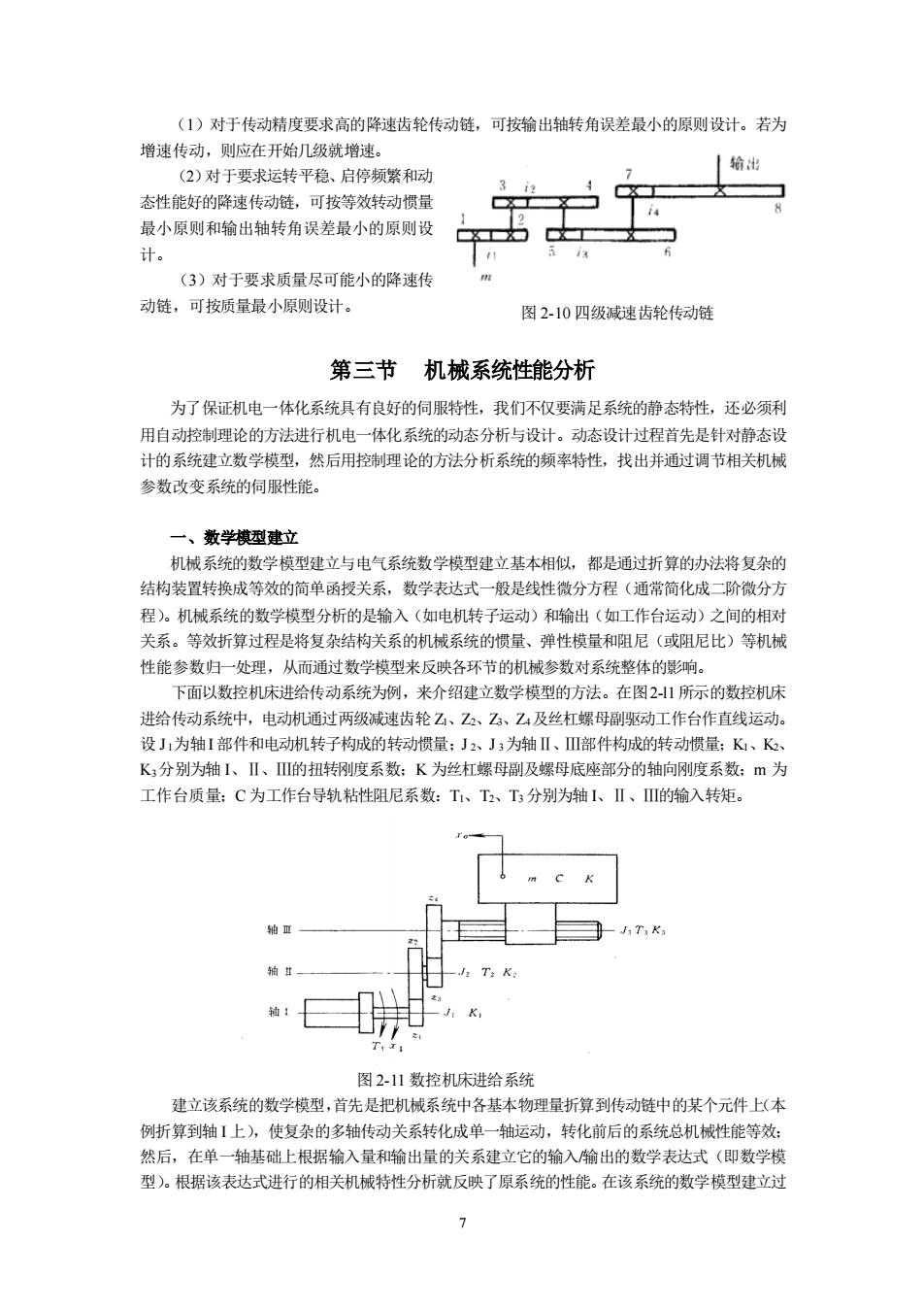
(1)对于传动精度要求高的降速齿轮传动链,可按输出轴转角误差最小的原则设计。若为 增速传动,则应在开始几级就增速 (2)对于要求运转平稳、启停须繁和动 给出 态性能好的降速传动链,可按等效转动惯量 最小原则和输出轴转角误差最小的原则设 计。 (3)对于要求质量尽可能小的降速传 动链,可按质量最小原则设计。 图2-10四级减速齿轮传动链 第三节机械系统性能分析 为了保证机电一体化系统具有良好的同服特性,我们不仅要满足系统的静态特性,还必须利 用自动控制理论的方法进行机电一体化系统的动态分析与设计。动态设计过程首先是针对静态设 十的系统建立数学模型,然后用控制理论的方法分析系统的频率特性, 找出并通过调节相关机械 参数改变系统的伺服性能。 一、数学棋型建立 机械系统的数学模型建立与电气系统数学模型建立基本相似,都是通过折算的办法将复杂的 结构装置转换成等效的简单函授关系,数学表达式一般是线性微分方程(通常简化成二阶微分方 程)。机械系统的数学模型分析的是输入(如电机转子运动)和输出(如工作台运动)之间的相对 关系。等效折算过程是将复杂结构关系的机械系统的惯量、弹性模量和阻尼(或阻尼比)等机械 性能参数归一处理,从而通过数学模型来反映各环节的机械参数对系统整体的影响。 下面以数控机床进给传动系统为例,来介绍建立数学模型的方法。在图21所示的数控机床 进给传动系统中,电动机通过两级减速齿轮乙、Z、☑、Z乙,及丝杠螺母副驱动工作台作直线运动, 设J为轴1部件和电动机转子构成的转动惯量:Jx、J,为轴Ⅱ、Ⅲ部件构成的转动惯量:K、K K,分别为轴【、Ⅱ、Ⅲ的扭转钢刚度系数:K为丝杠螺母刷及螺母底座部分的轴向钢刚度系数:m为 工作台质量:C为工作台导轨粘性阻尼系数:T、了、分别为轴1、Ⅱ、Ⅲ的输入转矩 图2.11数控机床讲给系线 建立该系统的数学模型,首先是把机械系统中各基本物理量折算到传动链中的某个元件上(本 例折算到轴1上),使复杂的多轴传动关系转化成单一轴运动,转化前后的系统总机械性能等效: 然后,在单一轴基础上根据输入量和输出量的关系建立它的输入输出的学表达式(即数学横 型)。根据该表达式进行的相关机械特性分析就反映了原系统的性能。在该系统的数学模型建立过 7
7 (1)对于传动精度要求高的降速齿轮传动链,可按输出轴转角误差最小的原则设计。若为 增速传动,则应在开始几级就增速。 (2)对于要求运转平稳、启停频繁和动 态性能好的降速传动链,可按等效转动惯量 最小原则和输出轴转角误差最小的原则设 计。 (3)对于要求质量尽可能小的降速传 动链,可按质量最小原则设计。 第三节 机械系统性能分析 为了保证机电一体化系统具有良好的伺服特性,我们不仅要满足系统的静态特性,还必须利 用自动控制理论的方法进行机电一体化系统的动态分析与设计。动态设计过程首先是针对静态设 计的系统建立数学模型,然后用控制理论的方法分析系统的频率特性,找出并通过调节相关机械 参数改变系统的伺服性能。 一、数学模型建立 机械系统的数学模型建立与电气系统数学模型建立基本相似,都是通过折算的办法将复杂的 结构装置转换成等效的简单函授关系,数学表达式一般是线性微分方程(通常简化成二阶微分方 程)。机械系统的数学模型分析的是输入(如电机转子运动)和输出(如工作台运动)之间的相对 关系。等效折算过程是将复杂结构关系的机械系统的惯量、弹性模量和阻尼(或阻尼比)等机械 性能参数归一处理,从而通过数学模型来反映各环节的机械参数对系统整体的影响。 下面以数控机床进给传动系统为例,来介绍建立数学模型的方法。在图2-l1所示的数控机床 进给传动系统中,电动机通过两级减速齿轮 Z1、Z2、Z3、Z4及丝杠螺母副驱动工作台作直线运动。 设 Jl为轴I 部件和电动机转子构成的转动惯量;J 2、J 3为轴Ⅱ、Ⅲ部件构成的转动惯量;K1、K2、 K3分别为轴 I、Ⅱ、Ⅲ的扭转刚度系数;K 为丝杠螺母副及螺母底座部分的轴向刚度系数;m 为 工作台质量;C 为工作台导轨粘性阻尼系数:T1、T2、T3 分别为轴 I、Ⅱ、Ⅲ的输入转矩。 图 2-11 数控机床进给系统 建立该系统的数学模型,首先是把机械系统中各基本物理量折算到传动链中的某个元件上(本 例折算到轴 I 上),使复杂的多轴传动关系转化成单一轴运动,转化前后的系统总机械性能等效; 然后,在单一轴基础上根据输入量和输出量的关系建立它的输入/输出的数学表达式(即数学模 型)。根据该表达式进行的相关机械特性分析就反映了原系统的性能。在该系统的数学模型建立过 图 2-10 四级减速齿轮传动链

程中,我们分别针对不同的物理量(如人、K、“)求出相应的折算等效值。 机械装置的质量(惯量、弹性模量和阻尼等机械特性参数对系统的影响是线性叠加关系,因 此在研究各参数对系统影响时,可以假设其它参数为理想状态,单独考虑特性关系。下面就基本 机械性能参数,分别时论转动惯量、弹性模量和阻尼的折算过程。 1、转动惯量的折算 把轴【、Ⅱ、上的转动惯量和工作台的质量都折算到轴【上,作为系统的等效转动惯量。 设T、了、了分别为轴1、Ⅱ、Ⅲ的负载转矩0小“公“,分别为轴【、【、Ⅲ的角速度:v为 工作台位移时的线速度。 (1)【、Ⅱ、Ⅲ轴转动惯量的折算根据动力平衡原理,【、Ⅱ、Ⅲ轴的力平衡方程分别是: T=J +T (2-8) T3=J2警+ (2-9) T3=J3+73 (2-10) 因为轴Ⅱ的输入转矩T2是由轴【上的负载转矩获得,且与它们的转速成反比,所以 T2=子T 又根据传动关系有 02=01 把T2和@2值代入式2-9,并将式2-8中的T也带入,整理得 T=J,(传}2警+ (2-11) 同理 =,层X+ (2-12) (2)工作台质量折算到I轴在工作台与丝杠间,了驱动丝杠使工作台运动。 根据动力平衡关系有 T2π=m(Φ)L 式中 工作台线速度 L一一丝杠导程。 即丝杠转动一周所做的功等于工作台前进一个导程时其惯性力所做的功。 又根据传动关系有 v=六03=(号2)0 把v值代入上式整理后得 ,=(会)'(停)m会 (2-13) (3)折算到轴1上的总转动惯量把式(2-11(2-12)、(2-13)代入式(28)(2-9)(2-10), 8
8 程中,我们分别针对不同的物理量(如 J、K、ω)求出相应的折算等效值。 机械装置的质量(惯量)、弹性模量和阻尼等机械特性参数对系统的影响是线性叠加关系,因 此在研究各参数对系统影响时,可以假设其它参数为理想状态,单独考虑特性关系。下面就基本 机械性能参数,分别讨论转动惯量、弹性模量和阻尼的折算过程。 1、转动惯量的折算 把轴 I、Ⅱ、Ⅲ上的转动惯量和工作台的质量都折算到轴 I 上,作为系统的等效转动惯量。 设 ' T1 、 ' T2 、 ' T3 分别为轴I、Ⅱ、Ⅲ的负载转矩,ω1、ω2、ω3分别为轴I、Ⅱ、Ⅲ的角速度;υ为 工作台位移时的线速度。 (1)I、Ⅱ、Ⅲ轴转动惯量的折算 根据动力平衡原理,I、Ⅱ、Ⅲ轴的力平衡方程分别是: ' 1 1 1 1 T J T dt d = + (2-8) ' 2 2 2 2 T J T dt d = + (2-9) ' 3 3 3 3 T J T dt d = + (2-10) 因为轴Ⅱ的输入转矩T2 是由轴 I 上的负载转矩获得,且与它们的转速成反比,所以 2 1 1 T z 2 T z = 又根据传动关系有 2 1 2 z 1 z = 把 T2 和ω2 值代入式 2-9,并将式 2-8 中的 T1 也带入,整理得 ( ) ' 2 2 2 ' 1 2 1 1 2 `1 T J ( ) z T z dt d z z = + (2-11) 同理 ( ) ' 3 2 3 ' 2 4 1 3 4 3 2 1 T J ( )( ) T z z dt d z z z z = + (2-12) (2)工作台质量折算到 I 轴 在工作台与丝杠间, ' T3 驱动丝杠使工作台运动。 根据动力平衡关系有 T m L dt dv 2 ( ) ' 3 = 式中 υ —— 工作台线速度; L —— 丝杠导程。 即丝杠转动一周所做的功等于工作台前进一个导程时其惯性力所做的功。 又根据传动关系有 2 3 2 1 ( ) 4 3 2 1 z z z L L z v = = 把 v 值代入上式整理后得 dt d z z z L z T m 1 4 3 2 1 ( ) ( ) 2 2 ' 3 = (2-13) (3)折算到轴Ⅰ上的总转动惯量 把式(2-11)、(2-12)、(2-13)代入式(2-8)(2-9)(2-10)

消去中间变量并整理后求出电机输出的总转矩T为 T=+J2()2+J(经)2+m()2()2]绘=J2会 (2-14) 式中 J上=J+J,(+J,(停)2+m倍)(会) (2-15) 上为系环节的转动惯量(成质量折算到1上的总等效动损量。其中,学 J,修引,分为,转动量和工作台质量折算到1鞋上的新转动损量。 2、粘性阻尼系数的折算 机械系统工作过程中,相互运动的元件间存在着阻力,并以不同的形式表现出来,如摩擦 力、流体阳力以及负载阻力等,这些阻力在建模时需要折算成与速度有关的粘滞阻尼力。 当工作台均速转动时,轴Ⅲ的驱动转矩T完全用来克服粘滞阻尼力的消耗。考虑到其它各环 节的摩擦损失比工作台导轨的摩擦损失小得多,故只计工作台导轨的粘性阻尼系数C。根据工作 台与丝杠之间的动力平衡关系有: T,2x=CvL 即丝杠转一周T所作的功,等于工作台前进一个导程时其阻尼力所作的功。 根据力学原理和传动关系有: T=(臣)2÷C0,=Co, (2-16) 式中C'一工作台导轨折算到轴1上的粘性阻力系数 C=停)P℃ (2-17) 3、弹性变形系数的折算 机械系统中各元件在工作时受力或力矩的作用,将产生轴向伸长、压缩或扭转等弹性变形 这些变形将影响到整个系统的桔度和动态特性。建模时要将其折算成相应的扭转刚度系数或轴向 刚度系数。 上中,应先将冬轴的转角都折算到轴 上来,丝杠与工作台之间的轴向弹性变形会使轴 产生一个附加扭转角,也应折算到轴1上,然 后求出轴1的总扭转度系数。同样,当系统在 无阻尼状态下,T、五、T等输入转矩都用来 -a 克服机构的弹性变形。 (1)轴向刚度的折算当系统承担负载 后,丝杠螺母副和螺母座都会产生轴向弹性变形 图212弹性变形的等效图 图212是它的等效作用图。在丝杠左端输入转矩 工的作用下,丝杠和工作台之间的弹性变形为6,对应的丝杠附加扭转角为△日,。根据动力平衡 9
9 消去中间变量并整理后求出电机输出的总转矩 T1 为 dt d dt L d z z z z z z z z z z T J J J m J 1 1 4 3 2 1 4 3 2 1 2 1 [ ( ) ( ) ( ) ( ) ] 2 2 2 2 3 2 1 1 2 = + + + = (2-14) 式中 J = 2 2 2 2 3 2 1 2 ( ) ( ) ( ) ( ) 4 3 2 1 4 3 2 1 2 1 L z z z z z z z z z z J + J + J + m (2-15) J 为系统各环节的转动惯量(或质量)折算到轴 I 上的总等效转动惯量。其中 2 2 1 2 ( ) Z Z J 、 ( ) 2 3 4 3 2 1 Z Z Z Z J 、 ( ) 2 2 2 4 3 2 1 L Z Z Z Z m 分别为Ⅱ、Ⅲ轴转动惯量和工作台质量折算到I 轴上的折算转动惯量。 2、粘性阻尼系数的折算 机械系统工作过程中,相互运动的元件间存在着阻力,并以不同的形式表现出来,如摩擦阻 力、流体阻力以及负载阻力等,这些阻力在建模时需要折算成与速度有关的粘滞阻尼力。 当工作台均速转动时,轴Ⅲ的驱动转矩 T3 完全用来克服粘滞阻尼力的消耗。考虑到其它各环 节的摩擦损失比工作台导轨的摩擦损失小得多,故只计工作台导轨的粘性阻尼系数 C。根据工作 台与丝杠之间的动力平衡关系有: T3 2 = CvL 即丝杠转一周 T3所作的功,等于工作台前进一个导程时其阻尼力所作的功。 根据力学原理和传动关系有: ( ) 1 ' 1 2 2 2 1 ( ) 3 4 1 T 2 z L C C z z z = = (2-16) 式中 C′——工作台导轨折算到轴 I 上的粘性阻力系数 C C L z z z z 2 2 ' 2 ( ) ( ) 3 4 1 2 = (2-17) 3、弹性变形系数的折算 机械系统中各元件在工作时受力或力矩的作用,将产生轴向伸长、压缩或扭转等弹性变形, 这些变形将影响到整个系统的精度和动态特性。建模时要将其折算成相应的扭转刚度系数或轴向 刚度系数。 上例中,应先将各轴的扭转角都折算到轴I 上来,丝杠与工作台之间的轴向弹性变形会使轴 Ⅲ产生一个附加扭转角,也应折算到轴 I 上,然 后求出轴 I 的总扭转刚度系数。同样,当系统在 无阻尼状态下,T1 、T2 、T3等输入转矩都用来 克服机构的弹性变形。 (1)轴向刚度的折算 当系统承担负载 后,丝杠螺母副和螺母座都会产生轴向弹性变形, 图 2-12是它的等效作用图。在丝杠左端输入转矩 T3 的作用下,丝杠和工作台之间的弹性变形为 ,对应的丝杠附加扭转角为 3 。根据动力平衡 图 2-12 弹性变形的等效图

原理和传动关系,在丝杠轴Ⅲ上有: T,2π=K 6=经L 所以 T3=()2K△0=K△8 式中K'一一附加扭转刚度系数 K=K (2-18) (2)扭转刚度系数的折算设日,、日2、日,分别为抽【、Ⅱ、Ⅲ在输入转矩T、T2、T 的作用下产生的扭转角。根据动力平衡原理和传动关系有 8=元 8,=2=)片 6=是-修虎 由于丝杠和工作台之间轴向弹性变形使轴附加了一个扭转角△日,因此轴上的实际扭转 角0m为:0m=83+△0 将8、△8值代入,则有 0=爱+是=得X+ 将各轴的扭转角折算到轴1上得轴I的总扭转角 0=日+售月,+色pm 将0,、02、Bm值代入上式有 0=产++追(G+江=货+太+层产佑+加=是(2.19 式中KΣ一一折算到轴【上的总扭转刚度系数 K= 太+学专+(学若P(店+女) (2-20) 4、建立系统的数学模型 根据以上的参数折算,建立系统动力平衡方程和推导数学模型。 设输入量为轴I的输入转角X:输出量为工作台的线位移X0。根据传动原理,把X折算成 轴1的输出角位移Φ。在轴上根据动力平衡原理有 10
10 原理和传动关系,在丝杠轴Ⅲ上有: L T K L 2 3 3 2 = = 所以 3 ' 3 2 2 1 3 ( ) T = K = K 式中 K′——附加扭转刚度系数 K ( ) K 2 2 ' 1 = (2-18) (2)扭转刚度系数的折算 设 1、 2 、 3 分别为轴 I、Ⅱ、Ⅲ在输入转矩 T1 、T2、、T3 的作用下产生的扭转角。根据动力平衡原理和传动关系有 ( ) ( ) 3 1 3 4 1 2 3 3 2 1 1 2 2 2 1 1 3 2 1 K T Z Z Z Z K T K T z z K T K T = = = = = 由于丝杠和工作台之间轴向弹性变形使轴Ⅲ附加了一个扭转角 3 ,因此轴Ⅲ上的实际扭转 角 Ⅲ为: Ⅲ= 3 + 3 将 3、 3 值代入,则有 1 1 1 ( )( )' 3 3 4 1 2 ' 3 3 3 T K z K z z z K T K T III = + = + 将各轴的扭转角折算到轴 I 上得轴I 的总扭转角 ( ) ( ) z III z z z z z 3 4 1 2 1 2 = 1 + 2 + 将 1、 2 、 III 值代入上式有: ( ) ( ) ( ) = + + + = + + + = K T z K K z z z z K z z K K K z z z K T z z K T T T 1 ' 3 3 4 1 2 ! 2 2 1 ' 3 3 4 1 2 2 1 1 2 1 1 1 1 2 1 1 2 1 1 1 1 2 2 ( ) [ ( ) ( )] (2-19) 式中 K ——折算到轴I 上的总扭转刚度系数 ( ) ( ) ( ) 1 ' 1 3 2 1 3 4 1 2 2 2 1 1 2 1 1 K Z K Z Z Z Z K Z K K + + + = (2-20) 4、建立系统的数学模型 根据以上的参数折算,建立系统动力平衡方程和推导数学模型。 设输入量为轴 I 的输入转角 Xi;输出量为工作台的线位移 Xo。根据传动原理,把 Xo 折算成 轴 I 的输出角位移 。在轴I 上根据动力平衡原理有