
实验2传热问题的数值计算 [计算问题1] 有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如图2-1所示。假设在垂 直纸面方向上,冷空气及砖墙的温度变化很小,可以近似地予以忽略。在下列两种情况 下,试计算:(1)砖墙横截面上的温度分布:(2)垂直于纸面方向的每米长度上通过砖 墙的导热热量。 第一种情况:内外表面温度均匀分布,维持在0°C及30°C: 第二种情况:内外表面均为第三类边界条件,且己知 tn=30°C,么=10w/m2.C,‘n=10C,4=4wm2.C, 砖墙的导热系数为=0.53W/八m°C: 2.0m 中中工 工中工中工中中中工中 ,tn 1.2m 3.0m 图2-1砖砌长方形通道 提示与建议: 网格节点的划分与传热学实验指导书中“二维导热物体温度场的电模拟实验”的划 分相一致,且h、,之值以学生所做实验的设备上表明的值为依据,把数值计算结果 与电模拟实验之值相比较。 [计算问题2] 有一空调房间,采用上面送风、下面回风的气流组织方式。取出一个截面当作二维
实验 2 传热问题的数值计算 [计算问题 1] 有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如图 2-1 所示。假设在垂 直纸面方向上,冷空气及砖墙的温度变化很小,可以近似地予以忽略。在下列两种情况 下,试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖 墙的导热热量。 第一种情况:内外表面温度均匀分布,维持在 0 C o 及 30 C o ; 第二种情况:内外表面均为第三类边界条件,且已知 30 C o t f 1 = , 10W (m C) 2 o 1 h = , 10 C o t f 2 = , 4W (m C) 2 o 2 h = , 砖墙的导热系数为 0 53W (m C) o = . 。 图 2-1 砖砌长方形通道 提示与建议: 网格节点的划分与传热学实验指导书中“二维导热物体温度场的电模拟实验”的划 分相一致,且 h1、 h2 之值以学生所做实验的设备上表明的值为依据,把数值计算结果 与电模拟实验之值相比较。 [计算问题 2] 有一空调房间,采用上面送风、下面回风的气流组织方式。取出一个截面当作二维 2 .0m 3 .0m 1 .2m 2 .2m 1 f 1 h , t 2 f 2 h , t
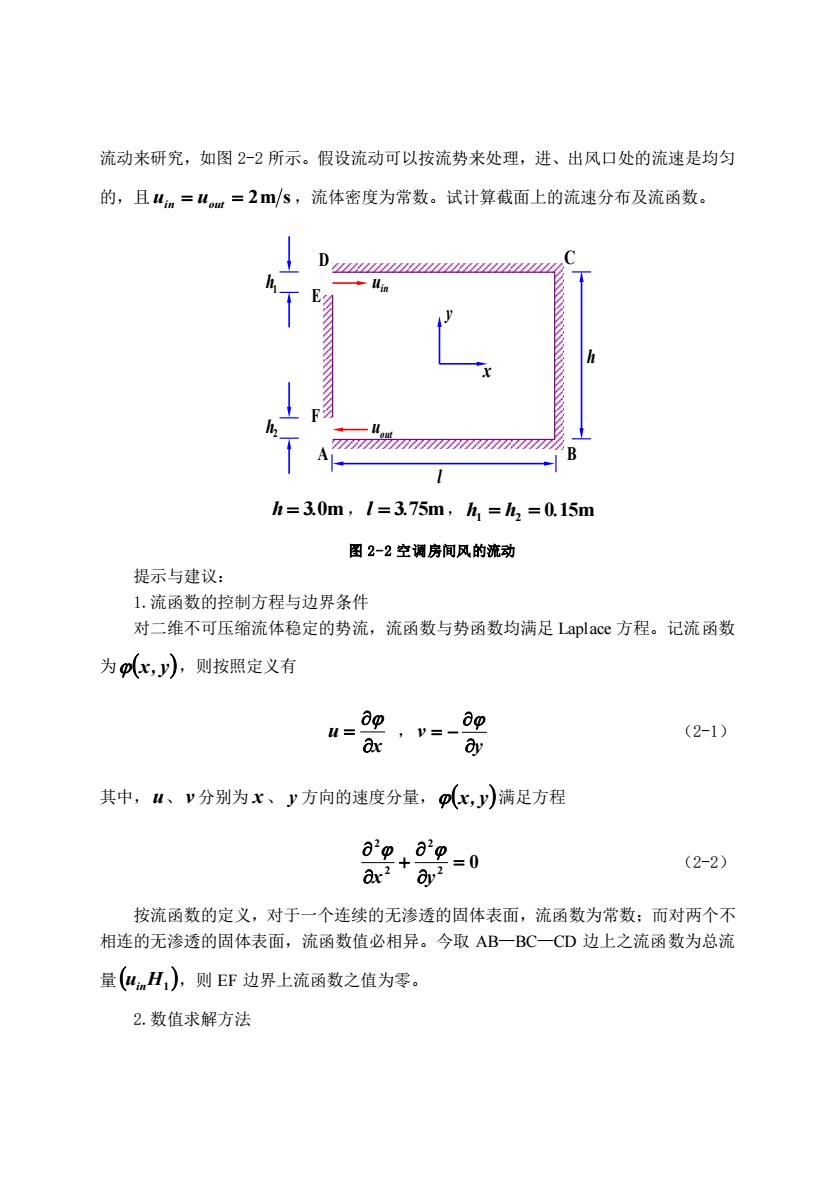
流动来研究,如图2-2所示。假设流动可以按流势米处理,进、出风口处的流速是均匀 的,且4n=4=2ms,流体密度为常数。试计算截面上的流速分布及流函数。 D h=30m,1=3.75m,h=h2=0.15m 图2-2空调房间风的流动 提示与建议: 1.流函数的控制方程与边界条件 对二维不可压缩流体稳定的势流,流函数与势函数均满足Laplace方程。记流函数 为(,y),则按照定义有 w-0e v=-0g (2-1) 其中,4、v分别为x、y方向的速度分量,(x,y)满足方程 8+8-0 (2-2) 按流函数的定义,对于一个连续的无渗透的固体表面,流函数为常数:而对两个不 相连的无渗透的固体表面,流函数值必相异。今取AB一BC一CD边上之流函数为总流 量(4H),则EF边界上流函数之值为零。 2.数值求解方法
流动来研究,如图 2-2 所示。假设流动可以按流势来处理,进、出风口处的流速是均匀 的,且 = = 2m s uin uout ,流体密度为常数。试计算截面上的流速分布及流函数。 h = 3.0m , l = 3.75m, h1 = h2 = 0.15m 图 2-2 空调房间风的流动 提示与建议: 1.流函数的控制方程与边界条件 对二维不可压缩流体稳定的势流,流函数与势函数均满足 Laplace 方程。记流函数 为 (x, y) ,则按照定义有 x u = , y v = − (2-1) 其中, u、 v 分别为 x 、 y 方向的速度分量, (x, y) 满足方程 0 2 2 2 2 = + x y (2-2) 按流函数的定义,对于一个连续的无渗透的固体表面,流函数为常数;而对两个不 相连的无渗透的固体表面,流函数值必相异。今取 AB—BC—CD 边上之流函数为总流 量 ( ) uinH1 ,则 EF 边界上流函数之值为零。 2.数值求解方法 A B D C x y h 1 h 2 h in u out u E F l

取△x=△y=0.15(m),则A、F、E、D四点正好在四条网格线上。这样,上述势 流问题相当于一个第一类边界条件的二维、稳态、常物性、无内热源的导热问题。采用 Gauss迭代法解出g,)后,可按定义计算各节点上的,j)与(,)。采用中心差分 时,有 ,)=+小-j-) (2-3) 2△y 6,)=t+l,》-1,) (2-4) 2Ax 画等流函数图时,可在p=0与p=0.3m'/s(垂直于纸面方向取单位厚度)之间 取五个中间值,即Q.05、0.1、0.15、0.2及0.25,画出这五条等流函数线 [计算问题3] 设在如图2-3所示的长方形截面的通道中,有空气充分发展的层流运动。试用数值 计算方法,确定截面上主流方向速度w的分布规律,并计算∫·R之值,其中∫为阻 力系数。取a/b=1及0.5两种情形。 b 国2-3长方形通道中空气流动
取 Δx = Δy = 0.15(m) ,则 A、F、E、D 四点正好在四条网格线上。这样,上述势 流问题相当于一个第一类边界条件的二维、稳态、常物性、无内热源的导热问题。采用 Gauss 迭代法解出 (i, j) 后,可按定义计算各节点上的 u(i, j) 与 v(i, j) 。采用中心差分 时,有 ( ) ( ) ( ) y i, j i, j u i, j 2Δ + 1 − − 1 = (2-3) ( ) ( ) ( ) x i , j i , j v i, j 2Δ + 1 − − 1 = (2-4) 画等流函数图时,可在 = 0 与 0 3m s 3 = . (垂直于纸面方向取单位厚度)之间 取五个中间值,即 0.05 、0.1、0.15 、0.2 及 0.25 ,画出这五条等流函数线。 [计算问题 3] 设在如图 2-3 所示的长方形截面的通道中,有空气充分发展的层流运动。试用数值 计算方法,确定截面上主流方向速度 w 的分布规律,并计算 f Re 之值,其中 f 为阻 力系数。取 a b = 1 及 0.5 两种情形。 图 2-3 长方形通道中空气流动 u v w x y a z b

提示与建议: 1.控制方程与边界条件 :方向的动量方程为 8'w 82w82w (2-5) 对于流动的充分发展段,有 =v=0, a°-0 (2-6) 且在同一截面上压力可视为常数,于是动量方程可简化为 供+光 (2-7) 在充分发展段,p仙为常数,于是可定义一个无量纲速度 W=Lov (2-8) 同时定义 x=若y= (2-9) 于是,控制方程化为 o'w a'w ax2+ar+1=0 (2-10) 在四条固体边界上 W=0 (2-11) 如利用对称性,取四分之一区域来计算,则在对称线上速度的法向导数等于零。由 此可见,这一问题相当于求解一个具有第一类边界条件(或第一、第二类混合边界条件 对四分之一计算区域)的二维、稳态、常物性、有内热源的导热问题。 f,Re之值可按定义计算
提示与建议: 1.控制方程与边界条件 z 方向的动量方程为 + + + = − + + 2 2 2 2 2 2 z w y w x w z p z w w y w v x w u (2-5) 对于流动的充分发展段,有 u = v = 0, = 0 z w (2-6) 且在同一截面上压力可视为常数,于是动量方程可简化为 z p y w x w d d 2 2 2 2 = + (2-7) 在充分发展段, dp dz 为常数,于是可定义一个无量纲速度 z p a w W d 2 d − = (2-8) 同时定义 a x X = , a y Y = (2-9) 于是,控制方程化为 1 0 2 2 2 2 + = + Y W X W (2-10) 在四条固体边界上 W = 0 (2-11) 如利用对称性,取四分之一区域来计算,则在对称线上速度的法向导数等于零。由 此可见,这一问题相当于求解一个具有第一类边界条件(或第一、第二类混合边界条件, 对四分之一计算区域)的二维、稳态、常物性、有内热源的导热问题。 f Re 之值可按定义计算

dp f.Re=-D. dz (2-12) 2 式中,wm为截面平均值。可见只要解出了w(,),即可得出f·Re之值。 2.数值求解方法 (1)在无量纲速度W的控制方程中,“1”为源项,在建立离散方程时切勿遗忘。 离散方程可用Gaus迭代法求解。 (2)在获得收敛的Wi,)后,再计算平均值Wm,并按上述公式计算f·R之值。 (3)f.Re的标准答案为:a/b=1时,f,Re=56.9;a/b=1/2时, f·Re=62.2。可用不同疏密度的网格进行计算,如取10×10、20×20等,并比较 网格疏密度的影响
2 2 2 2 d d = = − e m m e m e D v w w D w l z p f Re D (2-12) 式中, wm 为截面平均值。可见只要解出了 w(i, j) ,即可得出 f Re 之值。 2.数值求解方法 (1)在无量纲速度 W 的控制方程中,“1”为源项,在建立离散方程时切勿遗忘。 离散方程可用 Gauss 迭代法求解。 (2)在获得收敛的 W(i, j) 后,再计算平均值 Wm ,并按上述公式计算 f Re 之值。 ( 3 ) f Re 的 标准 答案 为: a b = 1 时 , f Re = 56.9 ; a b = 1 2 时 , f Re = 62.2 。可用不同疏密度的网格进行计算,如取 1010 、20 20 等,并比较 网格疏密度的影响