
实验6角系数的几何法测量 [实验目的 1.巩固辐射传热理论知识,深入理解角系数的几何意义及性质: 2.了解测定辐射传热角系数的原理和方法: 3.使用角系数测定仪测量角系数,分析影响角系数的因素。 「实验原理] 角系数是辐射传热、照明工程以及太阳能利用中经常遇到的重要参数,它表示从漫 射表面发出的辐射能中,到达某一表面的百分比。角系数与辐射面和吸收面的形状、大 小、相对位置有关,而与两表面的辐射及吸收性质无关,是一个纯几何因子。对规则形 状和特殊相对位置的表面,可以通过计算或查表等方法得到其角系数。但对不规则形状 和不规则相对位置的表面,通常只能由实验测定角系数。 0 9 d40 图6-1用几何法分析角系数的示意国 如图6-1所示,微元表面d4对d4,的角系数可表示为 Xcos cos (6-1) 上式也可以用下面的几何分析法获得。以d4的中心为球心,作半径为R的半球壳
实验 6 角系数的几何法测量 [实验目的] 1.巩固辐射传热理论知识,深入理解角系数的几何意义及性质; 2.了解测定辐射传热角系数的原理和方法; 3.使用角系数测定仪测量角系数,分析影响角系数的因素。 [实验原理] 角系数是辐射传热、照明工程以及太阳能利用中经常遇到的重要参数,它表示从漫 射表面发出的辐射能中,到达某一表面的百分比。角系数与辐射面和吸收面的形状、大 小、相对位置有关,而与两表面的辐射及吸收性质无关,是一个纯几何因子。对规则形 状和特殊相对位置的表面,可以通过计算或查表等方法得到其角系数。但对不规则形状 和不规则相对位置的表面,通常只能由实验测定角系数。 图 6-1 用几何法分析角系数的示意图 如图 6-1 所示,微元表面 dA1 对 dA2 的角系数可表示为 2 2 1 2 d1 d2 d cos cos A r X , = (6-1) 上式也可以用下面的几何分析法获得。以 dA1 的中心为球心,作半径为 R 的半球壳, 2 1 d 1 dA 2 dA 2 dA 2 dA R r 1 n 2 n O O

其在d4,所在平面上的投影为圆。再由微元面d4,的中心,作投射到微元面d4,周界的 射线,该射线在半球壳上切割出一个微元面4,有 ddcos (6-2) 将微元面d4投影到d4,所在平面(半球壳的底面)上,得到投影面积d4 R2 d4:=dA'cos:=d4z c0sc0sg (6-3) 把投影面积d4用圆面积πR2除,就得到 oscosd= (6-4) R2 π2 表达式(6-4)正是微元面d41对d42的角系数Xd1.d2。 d 图6-2角系数的图解计算法
其在 dA1 所在平面上的投影为圆。再由微元面 dA1 的中心,作投射到微元面 dA2 周界的 射线,该射线在半球壳上切割出一个微元面 dA2 ,有 2 2 2 2 2 d d cos r R A = A (6-2) 将微元面 dA2 投影到 dA1 所在平面(半球壳的底面)上,得到投影面积 dA2 2 1 2 2 2 2 1 2 d d cos d cos cos r R A = A = A (6-3) 把投影面积 dA2 用圆面积 2 R 除,就得到 2 2 d1 d2 1 2 2 2 d d cos cos A X , R r A = = (6-4) 表达式(6-4)正是微元面 dA1 对 dA2 的角系数 Xd1,d2 。 图 6-2 角系数的图解计算法 x y z A2 A2 A2 1 dA

这种几何分析法同样可以确定微元面d4对有限面积A,的角系数X2。如图6-2 所示,由d4的中心引向A,周界的射线,在半球壳上切割出面积A,而A;投影到d4 所在平面(半球壳的底面),得到投影面积A!。面积A与面积πR之比,则为d4,对 A,的角系数X2,即 X=装-小4=小,Xe6阿 2 如果求有限面积A对A,的角系数X2,可将面积A划分成微元面d4,求得微 元面d4,对面积A,的角系数X2,然后通过积分求得X2,即 X:=,X4=2pa4a466) 综上所述,可用几何分析法求得辐射传热的角系数。 [实验装置] 实验中所用的SE一Ⅱ型角系数测量仪由立杆、平行连杆、滑杆套管、记录笔、激 光源及设备底盘组成,其基本结构如图63所示。 M 图6-3角系数测量仪基本结构
这种几何分析法同样可以确定微元面 dA1 对有限面积 A2 的角系数 Xd1,2 。如图 6-2 所示,由 dA1 的中心引向 A2 周界的射线,在半球壳上切割出面积 A2 ,而 A2 投影到 dA1 所在平面(半球壳的底面),得到投影面积 A2 。面积 A2 与面积 2 R 之比,则为 dA1 对 A2 的角系数 Xd1,2 ,即 = = = 2 2 2 2 d1 d2 1 2 2 2 d1 2 d cos cos A , A , A X R r A X (6-5) 如果求有限面积 A1 对 A2 的角系数 X1,2 ,可将面积 A1 划分成微元面 dA1 ,求得微 元面 dA1 对面积 A2 的角系数 Xd1,2 ,然后通过积分求得 X1,2 ,即 2 2 1 1 2 1 d1 2 1 1 1 2 d d 1 cos cos d 1 1 1 2 A A A r X A A X A A A , , = = (6-6) 综上所述,可用几何分析法求得辐射传热的角系数。 [实验装置] 实验中所用的 SEJ—Ⅱ型角系数测量仪由立杆、平行连杆、滑杆套管、记录笔、激 光源及设备底盘组成,其基本结构如图 6-3 所示。 图 6-3 角系数测量仪基本结构 1 2 3 4 5 6 A B C M N
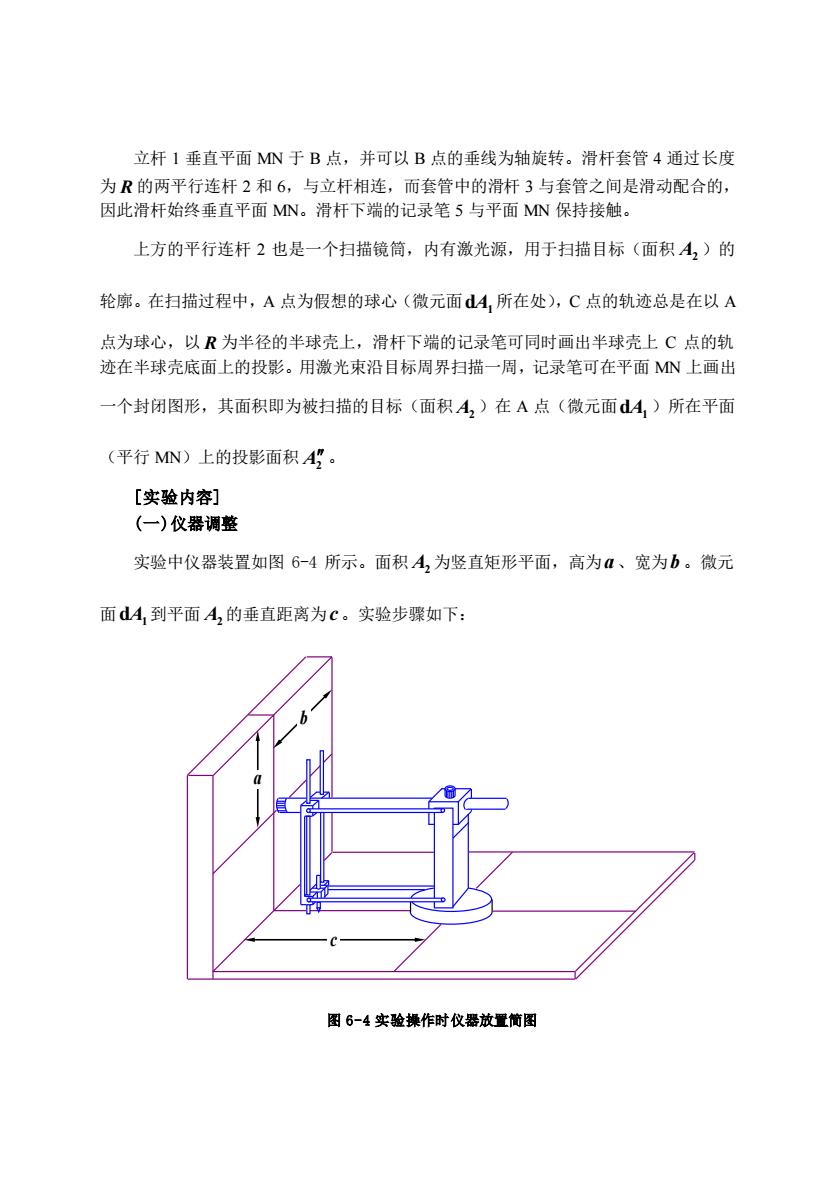
立杆1垂直平面MN于B点,并可以B点的垂线为轴旋转。滑杆套管4通过长度 为R的两平行连杆2和6,与立杆相连,而套管中的滑杆3与套管之间是滑动配合的, 因此滑杆始终垂直平面MN。滑杆下端的记录笔5与平面MN保持接触。 上方的平行连杆2也是一个扫描镜筒,内有激光源,用于扫描目标(面积A,)的 轮廓。在扫描过程中,A点为假想的球心(微元面dA,所在处),C点的轨迹总是在以A 点为球心,以R为半径的半球壳上,滑杆下端的记录笔可同时画出半球壳上C点的轨 迹在半球壳底面上的投影。用激光束沿目标周界扫描一周,记录笔可在平面MN上画出 一个封闭图形,其面积即为被扫描的目标(面积A,)在A点(微元面d4)所在平面 (平行MN)上的投影面积A?。 [实验内容] (一)仪器调整 实验中仪器装置如图6-4所示。面积A,为竖直矩形平面,高为a、宽为b。微元 面d4到平面A的垂直距离为C。实验步骤如下: 图6-4实验操作时仪器放置简图
立杆 1 垂直平面 MN 于 B 点,并可以 B 点的垂线为轴旋转。滑杆套管 4 通过长度 为 R 的两平行连杆 2 和 6,与立杆相连,而套管中的滑杆 3 与套管之间是滑动配合的, 因此滑杆始终垂直平面 MN。滑杆下端的记录笔 5 与平面 MN 保持接触。 上方的平行连杆 2 也是一个扫描镜筒,内有激光源,用于扫描目标(面积 A2 )的 轮廓。在扫描过程中,A 点为假想的球心(微元面 dA1 所在处),C 点的轨迹总是在以 A 点为球心,以 R 为半径的半球壳上,滑杆下端的记录笔可同时画出半球壳上 C 点的轨 迹在半球壳底面上的投影。用激光束沿目标周界扫描一周,记录笔可在平面 MN 上画出 一个封闭图形,其面积即为被扫描的目标(面积 A2 )在 A 点(微元面 dA1 )所在平面 (平行 MN)上的投影面积 A2 。 [实验内容] (一)仪器调整 实验中仪器装置如图 6-4 所示。面积 A2 为竖直矩形平面,高为 a 、宽为 b 。微元 面 dA1 到平面 A2 的垂直距离为 c 。实验步骤如下: 图 6-4 实验操作时仪器放置简图 a b c

1.取下角系数测量仪的包装箱盖板,将盖板有定位铜圈的面朝上平放在桌子上。在 盖板上铺上白纸,用定位铜圈压住。然后取出角系数测量仪,安放在定位铜圈上。 2.把仪器箱的底板竖直放置,与水平放置的盖板垂直。盖板紧靠箱体底板(距离c 最小),将盖板上的箭头与箱体底板上的箭头对准。 3.抬起记录笔,双手握住平衡块,用拇指按下红色按钮,将激光束仔细地扫描平面 A,的轮廓线。多次进行上述操作练习。 4.待操作熟练后,放下记录笔,调整记录笔的高度,使记录笔能够在白纸上画出痕 迹。然后将激光束仔细地扫描平面A,的轮廓线一周,让记录笔在白纸上画出一封闭图 形。注意记录距离℃。之后抬起记录笔,取下白纸,用面积测量仪测出封闭图形的面积 A,将其值除以圆面积πR,所得值即为测量的角系数X2。 5.改变盖板与箱体底板的距离,即调整距离c。重新安放白纸,重复实验步骤4, 测得新的角系数X2,比较两次测量结果,看看角系数与哪些因素有关。 6.记录仪器上标出的a、b及R值,理论计算角系数,并与实测结果进行比较,分 析产生误差的原因。 (二)测量数据 1= b= ,R= C= A=」 ,Xan2= c'= A=」 X2= [注意事项] 1.测量仪较重,轻拿轻放,小心掉地砸脚。 2.记录笔与白纸要接触紧密,否则很难画出封闭图形。 3.可以采用多种方法测得封闭图形的面积,以得到准确的面积。 [数据处理] 1.实验测量角系数
1.取下角系数测量仪的包装箱盖板,将盖板有定位铜圈的面朝上平放在桌子上。在 盖板上铺上白纸,用定位铜圈压住。然后取出角系数测量仪,安放在定位铜圈上。 2.把仪器箱的底板竖直放置,与水平放置的盖板垂直。盖板紧靠箱体底板(距离 c 最小),将盖板上的箭头与箱体底板上的箭头对准。 3.抬起记录笔,双手握住平衡块,用拇指按下红色按钮,将激光束仔细地扫描平面 A2 的轮廓线。多次进行上述操作练习。 4.待操作熟练后,放下记录笔,调整记录笔的高度,使记录笔能够在白纸上画出痕 迹。然后将激光束仔细地扫描平面 A2 的轮廓线一周,让记录笔在白纸上画出一封闭图 形。注意记录距离 c。之后抬起记录笔,取下白纸,用面积测量仪测出封闭图形的面积 A2 ,将其值除以圆面积 2 R ,所得值即为测量的角系数 Xd1,2 。 5.改变盖板与箱体底板的距离,即调整距离 c 。重新安放白纸,重复实验步骤 4, 测得新的角系数 Xd1,2 ,比较两次测量结果,看看角系数与哪些因素有关。 6.记录仪器上标出的 a 、b 及 R 值,理论计算角系数,并与实测结果进行比较,分 析产生误差的原因。 (二)测量数据 a = , b = , R = ; c = , A2 = , Xd1,2 = ; c = , A2 = , Xd 1,2 = 。 [注意事项] 1.测量仪较重,轻拿轻放,小心掉地砸脚。 2.记录笔与白纸要接触紧密,否则很难画出封闭图形。 3.可以采用多种方法测得封闭图形的面积,以得到准确的面积。 [数据处理] 1.实验测量角系数

A Xa2=R (6-7) 式中A一一测得的封闭图形的面积,m2: R一一连杆的长度(半球壳的半径),m。 2.理论计算角系数 1 (6-8) 2π 式中a一一矩形平面A,的高,m: b一一矩形平面A,的宽,m: c一一测量仪立柱中心到箱体底板的距离(微元面d4到平面A,的距离),m。 [问题思考] 1.由实验原理,用几何分析法推导出实验所给几何条件下角系数的理论计算公式。 2.根据角系数的几何分析法,如果微元面山4,到面积A,的距离小于连杆长度R 能否测量X2?怎样测量? 3.能否用测量仪测定微元面d4对与其距离c的同轴圆盘(直径为d)A,的角系 数X2?请用角系数分析法导出其理论计算式
2 2 d1 2 R A X , = (6-7) 式中 A2 ——测得的封闭图形的面积, 2 m ; R ——连杆的长度(半球壳的半径),m 。 2.理论计算角系数 + + − = − − 2 2 1 2 2 1 d1 2 tan tan 2 1 a c b a c c c b X , (6-8) 式中 a ——矩形平面 A2 的高, m ; b ——矩形平面 A2 的宽, m ; c——测量仪立柱中心到箱体底板的距离(微元面 dA1 到平面 A2 的距离),m 。 [问题思考] 1.由实验原理,用几何分析法推导出实验所给几何条件下角系数的理论计算公式。 2.根据角系数的几何分析法,如果微元面 dA1 到面积 A2 的距离小于连杆长度 R , 能否测量 Xd1,2 ?怎样测量? 3.能否用测量仪测定微元面 dA1 对与其距离 c 的同轴圆盘(直径为 d ) A2 的角系 数 Xd1,2 ?请用角系数分析法导出其理论计算式