
第四章 振动与波动
第四章 振动与波动

机械振动: 物体在一定的位置附近做来回往复的运动。 振动:任何一个物理量在某个确定的数值附近作 周期性的变化。 波动:振动状态在空间的传播。 任何复杂的振动都可 以看做是由若干个简 单而又基本的振动的 合成。这种简单而又 基本的振动形式称为 简谐运动
物体在一定的位置附近做来回往复的运动。 机械振动: 振动:任何一个物理量在某个确定的数值附近作 周期性的变化。 波动:振动状态在空间的传播。 任何复杂的振动都可 以看做是由若干个简 单而又基本的振动的 合成。这种简单而又 基本的振动形式称为 简谐运动
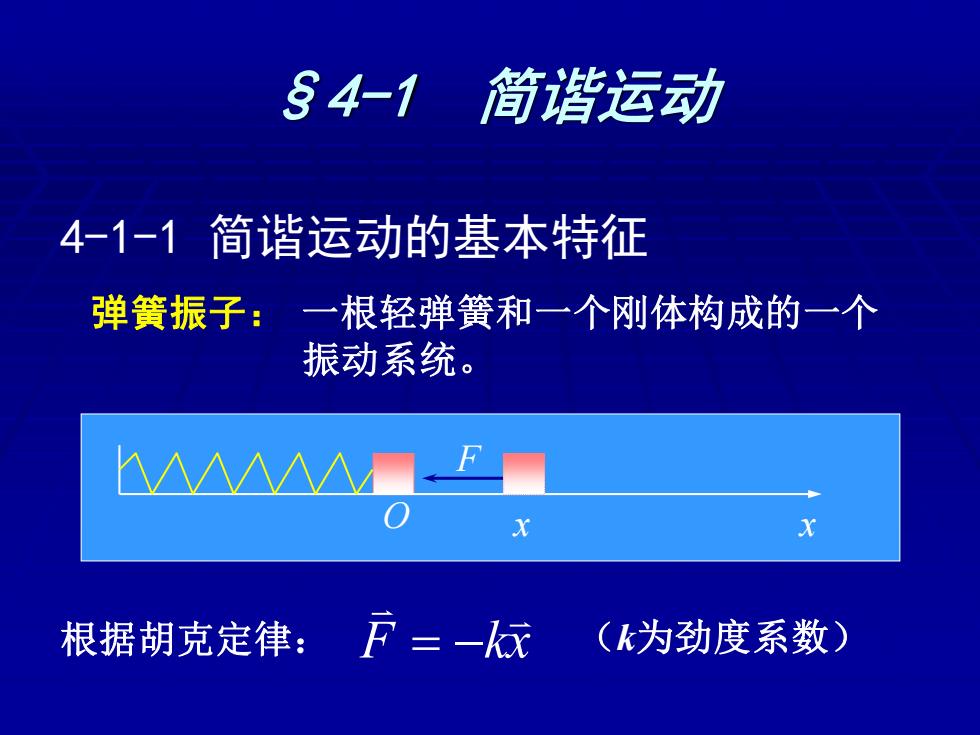
34-1 简谐运动 4-1-1简谐运动的基本特征 弹簧振子:一根轻弹簧和一个刚体构成的一个 振动系统。 M∧△∧Λ△■ X X 根据胡克定律:户=一 (k为劲度系数)
O x §4-1 简谐运动 4-1-1 简谐运动的基本特征 弹簧振子: 一根轻弹簧和一个刚体构成的一个 振动系统。 F x 根据胡克定律: F kx (k为劲度系数) = −

(1) 在弹性限度内,弹性力F和位移x成正比。 (2) 弹性力F和位移x恒反向,始终指向平衡位置。 恢复力:始终指向平衡位置的作用力 由牛顿第一定律: d?x F=m dt? =-kx 得: k 一X dt2 n =-02x dt?
恢复力: 始终指向平衡位置的作用力 (1) 在弹性限度内,弹性力F和位移x 成正比。 (2) 弹性力F和位移x 恒反向,始终指向平衡位置。 由牛顿第一定律: k x t x F = m = − 2 2 d d x m k t x = − 2 2 d d 得: 令 m k = x t x 2 2 2 d d = −

简谐运动表达式: x Acos(wt+p 简谐运动: 物体的运动遵从余弦(或正弦)规律。 简谐运动的三项基本特征: F=- d2x dr2 =-02x x=Acos(at+p)
简谐运动表达式: x = Acos(t +) 简谐运动: 物体的运动遵从余弦(或正弦)规律。 F kx = − x t x 2 2 2 d d = − x = Acos(t +) 简谐运动的三项基本特征:

简谐运动的速度: dx dt =-04s(ot+p)=0.c0s01+p+2 简谐运动的加速度: dv a= =-o2Acos(0t+p)=amc0s(0t+p土π) dt x,U,a
) 2 π sin( ) cos( d d = = − A t + = m t + + t x v v 简谐运动的速度: 简谐运动的加速度: cos( ) cos( π ) d d m 2 = = − A t + = a t + t a v O T t x x, v,a A − A a v O A 2

4-1-2 描述简谐运动的物理量 x Acos(ot+p) A:振幅 (最大位移,x=士A) 2元 0:角频率(圆频率) 0=2πy= T 频率:单位时间内完成全振动的次数。 周期T:完成一次全振动所经历的时间
4-1-2 描述简谐运动的物理量 x = Acos(t +) 周期 T:完成一次全振动所经历的时间。 A :振幅 (最大位移,x =±A ) :角频率 (圆频率) 频率 :单位时间内完成全振动的次数。 = 2π T 2π =

弹簧振子的频率: 2π 弹簧振子的周期: T- 2-2 k 结论:弹簧振子的振动频率和周期仅与振子本身的性 质(k和m)有关,而与其他因素无关。 由振动系统本身的固有属性所决定的频率和周 期称为固有频率和固有周期。 (ot+p):振动的“相位”。 p:振动的“初相位
:振动的“初相位 ” 。 ( t + ) :振动的“相位 ”。 弹簧振子的频率: m k 2π 1 = 弹簧振子的周期: k m T 2π 2π = = 结论:弹簧振子的振动频率和周期仅与振子本身的性 质(k 和 m)有关,而与其他因素无关。 由振动系统本身的固有属性所决定的频率和周 期称为固有频率和固有周期

dx 0= dt =-0Asmo1+p)=0.co@1+p+3 0m=0A 称为速度幅。 速度相位比位移相位超前元/2。 d a= dt =-o2Acos(ot+p)=cs(01+0±元) am =02A 称为加速度幅。 加速度与位移反相位
) 2 π sin( ) cos( d d = = − A t + = m t + + t x v v 称为速度幅。 速度相位比位移相位超前/2。 vm = A cos( ) cos( π ) d d m 2 = = − A t + = a t + t a v 称为加速度幅。 加速度与位移反相位。 a A 2 m =

比较: a=-@2Acos(@t+p) x Acos(ot+p) a=-@-x 即 =-02x dt? 结论:做简谐运动的质点,其加速度与位移恒成正比, 而方向相反
比较: a = − Acos(t +) 2 x = Acos(t +) 结论:做简谐运动的质点,其加速度与位移恒成正比, 而方向相反。 a x 2 = − 即 x t x 2 2 2 d d = −