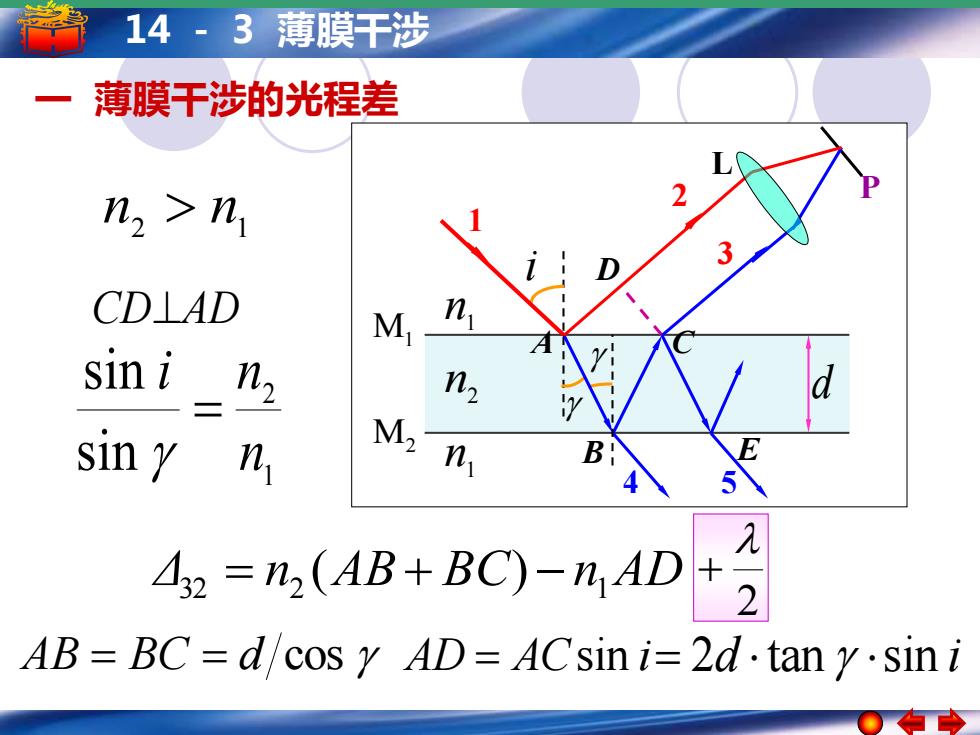
14·3薄膜干涉 薄膜干涉的光程差 n2>n1 CD⊥AD M n sin i 2 n sin y n M2 n 42=n(AB+BC)-nAD +2 AB BC=d/cos y AD=ACsin i=2d.tan y.sin i
14 - 3 薄膜干涉 P 1 n 1 n n2 M1 M2 d L 一 薄膜干涉的光程差 CD⊥AD Δ32 = n2 (AB + BC) − n1 AD AB = BC = d cos AD = ACsin i= 2d tan sin i 1 2 sin sin n i n = 2 + n2 n1 i D C 3 4 E 5 A 1 B 2
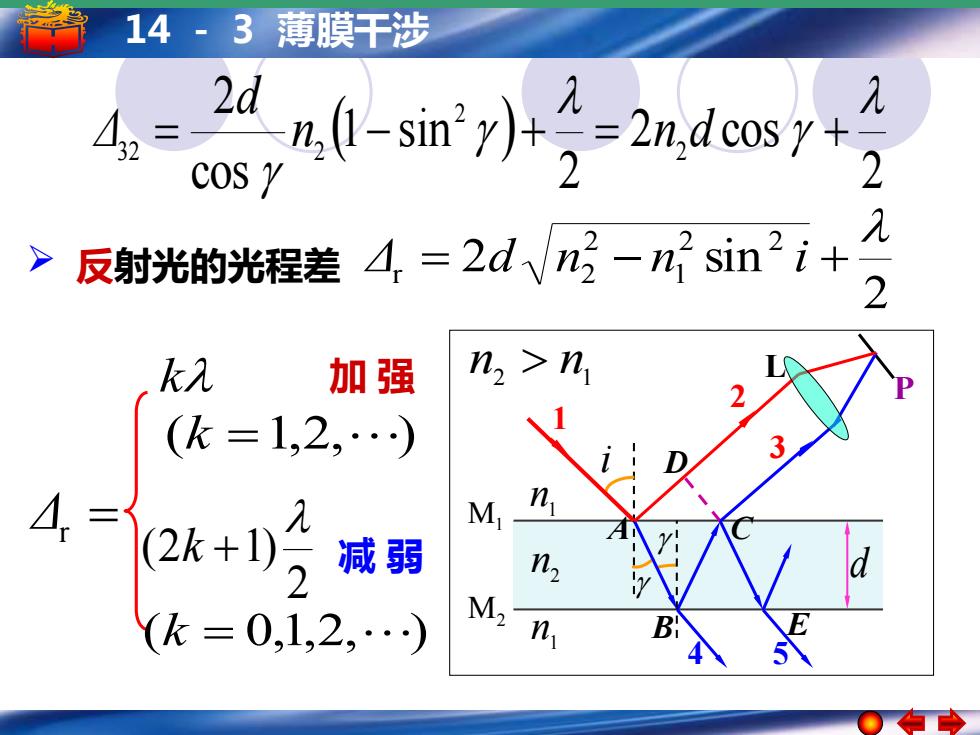
14-3薄膜干涉 ddind cos y 2 > 反射光的光程差4=2d√n-nsin2i+ 2 k入 加强 n >n 2 D (k=1,2,.) D 3 2k+0 M n 减弱 1n2 (k=0,1,2,.) M2 n
14 - 3 薄膜干涉 ( ) 2 2 cos 2 1 sin cos 2 2 2 32 2 = n − + = n d + d Δ 2 2 sin 2 2 1 2 r 2 ➢ 反射光的光程差 Δ = d n − n i + Δr = k 加 强 (k =1,2, ) 2 (2 1) k + 减 弱 (k = 0,1,2, ) P 1 n 1 n 2 n M1 M2 d L i D C 3 4 E 5 A 1 B 2 n2 n1

14-3 薄膜干涉 透镜不引起附加的光程差 焦平面 B
14 - 3 薄膜干涉 F A B o ➢ 透镜不引起附加的光程差 ' F A B 焦平面
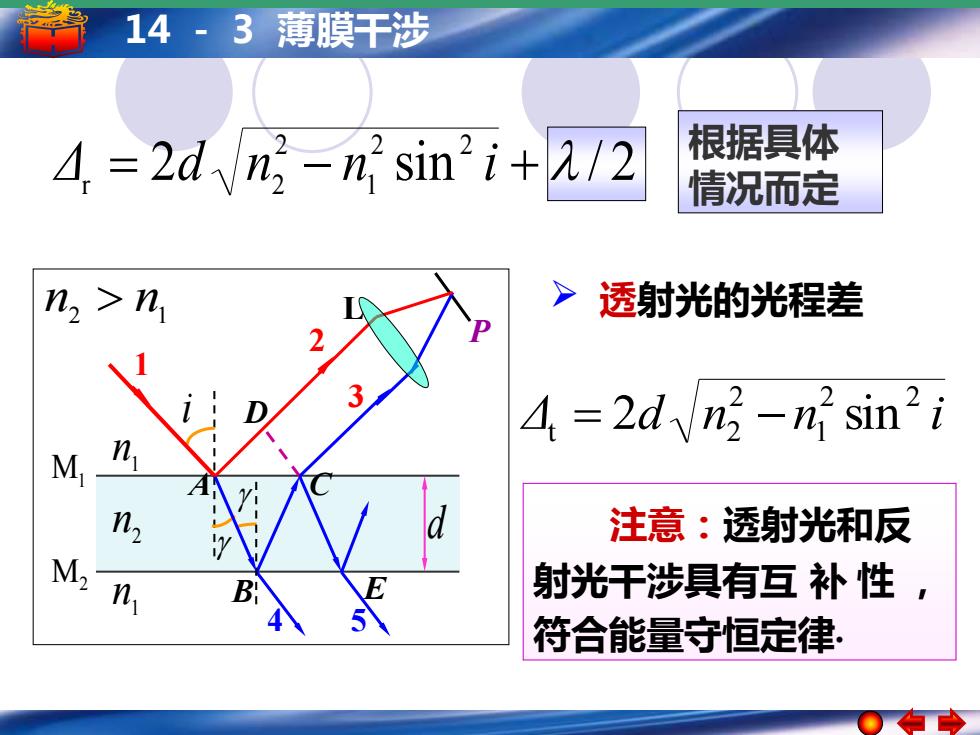
14-3薄膜干涉 4=2d n=n'sin'i+1/2 根据具体 情况而定 n>n >透射光的光程差 A=2dn-n sin2i 2 M n, 注意:透射光和反 M2 n B 射光干涉具有互补性, 符合能量守恒定律
14 - 3 薄膜干涉 Δ d n n i 2 2 1 2 t 2 = 2 − sin ➢ 透射光的光程差 注意:透射光和反 射光干涉具有互 补 性 , 符合能量守恒定律. 根据具体 情况而定 2 sin / 2 2 2 1 2 Δ r = d n2 − n i + P 1 n 1 n 2 n M1 M2 d L i D C 3 4 E 5 A 1 B 2 n2 n1
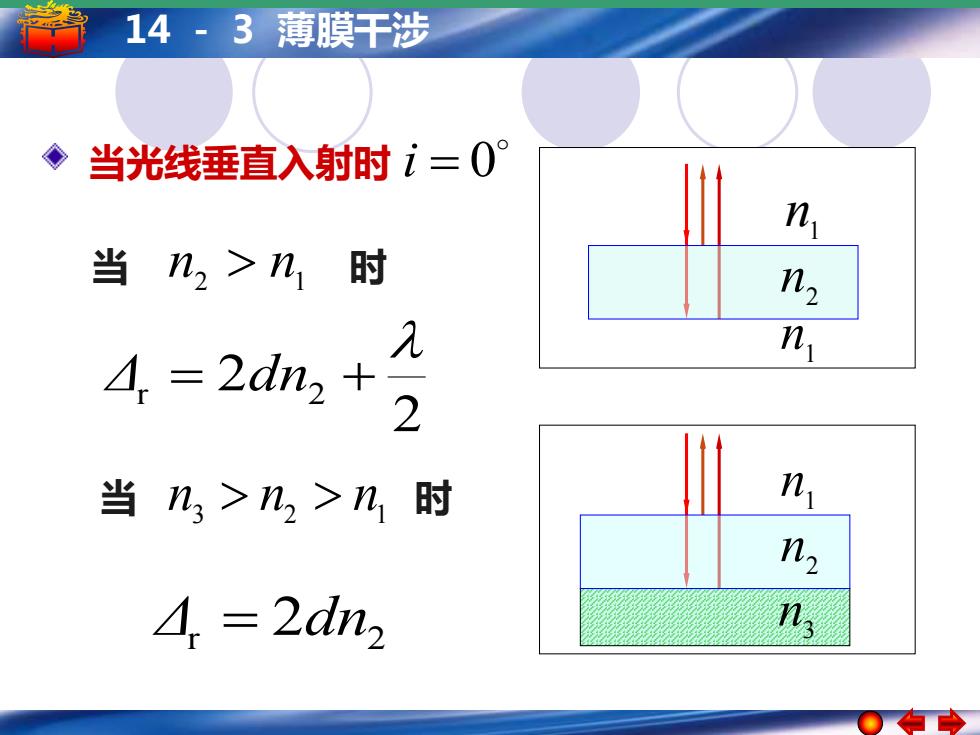
14·3薄膜干涉 当光线垂直入射时i=0° n 当n2>n1时 n n 4=2dn2+ 2 当n3>n2>n1时 n n 4,=2dn2 n
14 - 3 薄膜干涉 当光线垂直入射时 i = 0 2 r 2 2 Δ = dn + Δr = 2dn2 1 n 1 n 2 n 1 n n3 2 n 当 n2 n1 时 3 2 1 当 n n n 时

14-3薄膜干涉 例1在金属铝的表面,经常利用阳极氧化等方法形 成一层透明的氧化铝(Al2O3)薄膜,其折射率=1.80. 设一磨光的铝片表面形成了厚度d=250nm的透明氧化 铝薄层,问在日光下观察,其表面呈现什么颜色?(设 白光垂直照射到铝片上,铝的折射率小于氧化铝的折射 率.)解 △2=2nd+=k2 (k=1,2.) 2 2nd k=1,元=1800m = 1 k=2,2=600m k 2 k=3,元=300nm 表面呈橙红色 铝
14 - 3 薄膜干涉 例1 在金属铝的表面,经常利用阳极氧化等方法形 成一层透明的氧化铝 ( Al2 O3 ) 薄膜,其折射率n = 1.80. 设一磨光的铝片表面形成了厚度d = 250 nm的透明氧化 铝薄层,问在日光下观察,其表面呈现什么颜色?(设 白光垂直照射到铝片上,铝的折射率小于氧化铝的折射 率.)解 = nd + = k 2 12 2 12 n d 铝 2 1 2 − = k nd 3, 300 nm 2, 600 nm 1, 1800 nm = = = = = = k k k 表面呈橙红色 (k =1,2)

14-3 薄膜干涉 例2用波长为550nm的黄绿光照射到一肥皂膜上 沿与膜面成60°角的方向观察到膜面最亮。已知肥 皂膜折射率为1.33,求此膜至少是多厚?若改为垂 直观察,求能够使此膜最亮的光波长。 解:空气折射率nh≈1,肥皂膜 折射率n2=1.33。i=30° 反射光加强条件: 6=2dn-n sin2i+ =k2 2 、 解得: d= 2 2vn-n2 sin2i
14 - 3 薄膜干涉 例2 用波长为550nm的黄绿光照射到一肥皂膜上, 沿与膜面成60°角的方向观察到膜面最亮。已知肥 皂膜折射率为1.33,求此膜至少是多厚?若改为垂 直观察,求能够使此膜最亮的光波长。 解: d 60 空气折射率n1 ≈ 1,肥皂膜 折射率n2 = 1.33。i = 30° = d n − n i + = k 2 2 sin 2 2 1 2 2 反射光加强条件: n n i k d 2 2 1 2 2 2 sin 2 − − = 解得:

14-3薄膜干涉 肥皂膜的最小厚度(k=1) d= 4vn-n sin2i 550×109m =1.22×10m 4V1.332-12sin230° 2 垂直入射:6=2n,d+2=k以 2 2n,d 2=649.0m (k=1) 红 2 22=216.3m (k=2)不可见光
14 - 3 薄膜干涉 肥皂膜的最小厚度(k = 1) n n i d 2 2 1 2 2 4 − sin = 1.22 10 m 4 1.33 1 sin 30 550 10 m 7 2 2 2 9 − − = − = 垂直入射: = n d + = k 2 2 2 2 1 2 2 − = k n d 红 不可见光 649.0 nm ( 1) 1 = k = 216.3 nm ( 2) 2 = k =

14·3薄膜干涉 例3平面单色光垂直照射在厚度均匀的油膜上,油膜 覆盖在玻璃板上。所用光源波长可以连续变化,观察 到500nm与700nm两波长的光在反射中消失。油膜的 折射率为1.30,玻璃折射率为1.50,求油膜的厚度。 解:2nd=(2k+1)2 2nd=2k-)+2 2+空-(2k-2 k=3 d=6.73×10-4mm
14 - 3 薄膜干涉 例3 平面单色光垂直照射在厚度均匀的油膜上,油膜 覆盖在玻璃板上。所用光源波长可以连续变化,观察 到500 nm与700 nm 两波长的光在反射中消失。油膜的 折射率为1.30,玻璃折射率为1.50,求油膜的厚度。 解: 2 2 (2 1) 1 1 n d = k + 2 2 [2( 1) 1] 2 1 n d = k − + 2 (2 1) 2 (2 1) 1 2 k + = k − k = 3 6.73 10 mm −4 d = n1 n2

14-3薄膜干涉 增透膜和增反膜 利用薄膜干涉可以提高光学器件的透光率 。 例2为了增加透射率,求氟化镁膜的最小厚度 已知空气n,=1.00,氟化镁n2=1.38,2=550nm 解4,=2dn2=(2k+1) 23 2 取 k=0 减弱 n2 d d=dmin ≈100nm 玻璃n,>n, 4n2 氟化镁为增透膜 则4=2n2d+。=1(增强) 2
14 - 3 薄膜干涉 玻璃 3 2 n n d n1 2 n 氟化镁为增透膜 增透膜和增反膜 利用薄膜干涉可以提高光学器件的透光率 . 例 2 为了增加透射率 , 求氟化镁膜的最小厚度. 已知空气 1.00 , 氟化镁 , n1 = n2 =1.38 = 550 nm 23 解 减弱 2 2 (2 1) r 2 Δ = dn = k + 取 k = 0 2 min 4n d d = = 100nm 2 t 2 2 则 Δ = n d + = (增强)