之3 *3-9质心质心运动定律 质心 手榴弹质心(红点)的运动轨迹是抛物线 > 其余质点的运动:质心的平动十绕质心的转动
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 ➢ 其余质点的运动: 质心的平动 + 绕质心的转动 一 质心 手榴弹质心(红点)的运动轨迹是抛物线
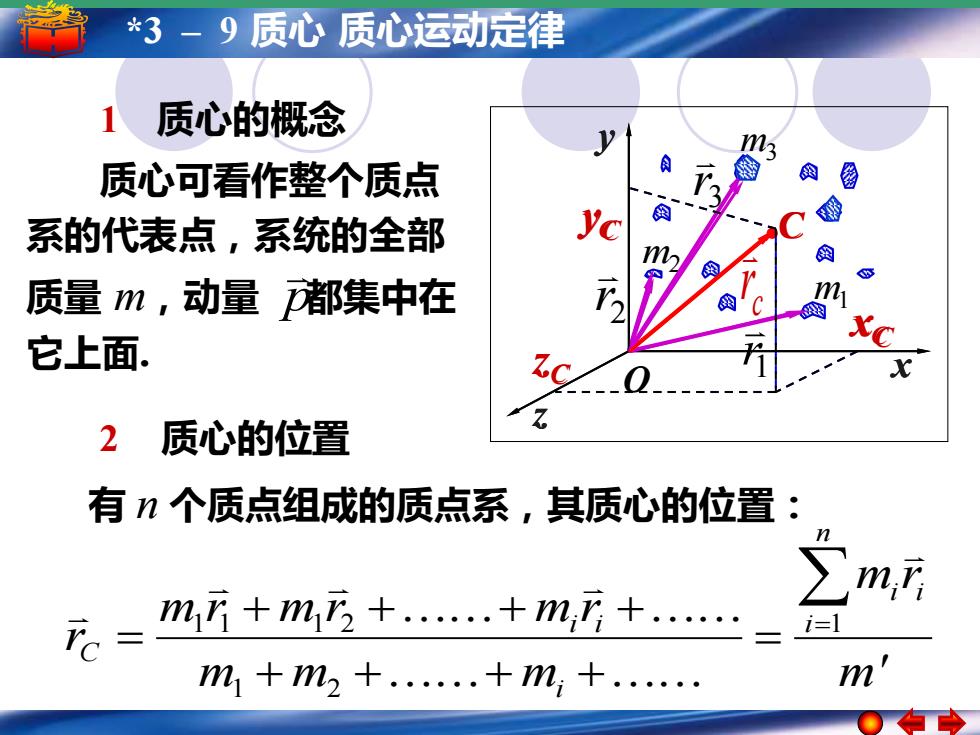
3-9质心质心运动定律 1 质心的概念 1 m 质心可看作整个质点 系的代表点,系统的全部 1 质量m,动量都集中在 m 它上面. 2 质心的位置 有个质点组成的质点系,其质心的位置: ∑m, m+m2+.+m,+. i=l m+m2+.+m,+. m
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 m ' m r m m m m r m r m r r i n i i i i i C = = + ++ + + ++ + = 1 1 2 1 1 1 2 有 n 个质点组成的质点系,其质心的位置: 2 质心的位置 1 质心的概念 质心可看作整个质点 系的代表点,系统的全部 质量 m,动量 都集中在 它上面. p m1 m2 m3 c r 1 r 2 r 3 r C O x y z xC yC zC x y z C yC xC C

*3-9质心质心运动定律 对质量离散分布的体系 n mxi ∑ yi mZi Xc= i=l yc= i=1 i=1 m' c m' m' 对质量连续分布的物体: Xc xdm m 说明 对密度均匀、形状对称的物体,其质心在 其几何中心
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 m' m x x i n i i C = = 1 m' m y y i n i i C = = 1 m' m z z i n i i C = = 1 = xdm m' xC 1 = ydm m' yC 1 = zdm m' z C 1 ➢ 对质量连续分布的物体: ➢ 对质量离散分布的体系: 对密度均匀、形状对称的物体,其质心在 其几何中心. 说明
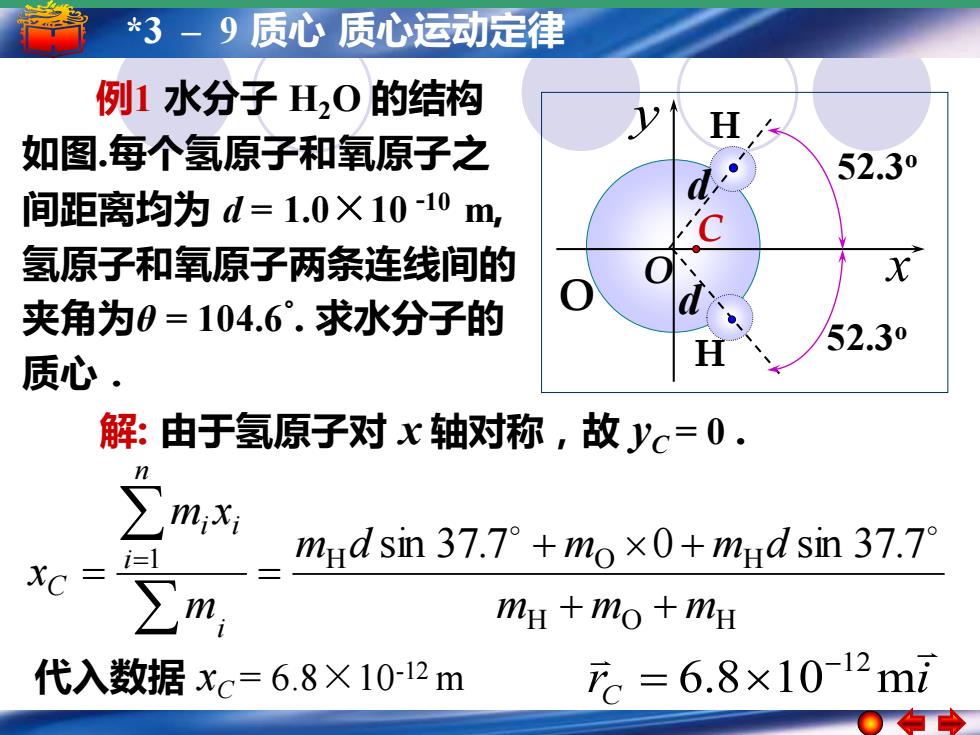
3-9质心质心运动定律 例1水分子H,0的结构 1 H 如图每个氢原子和氧原子之 52.30 间距离均为d=1.0×10-10m, C 氢原子和氧原子两条连线间的 夹角为0=104.6°.求水分子的 52.30 质心 解:由于氢原子对x轴对称,故yc=0. ∑m,x i mud sin37.7°+mo×0+mud sin37.7° ∑m, my mo mH 代入数据xc=6.8×10-12m F。=6.8×10-12mi
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 例1 水分子 H2O 的结构 如图.每个氢原子和氧原子之 间距离均为 d = 1.0×10 -10 m, 氢原子和氧原子两条连线间的 夹角为θ = 104.6° . 求水分子的 质心. O H H O x y C d d 52.3o 52.3o 解: 由于氢原子对 x 轴对称,故 yC = 0 . 代入数据 xC = 6.8×10-12 m r i C 6.8 10 m −12 = H O H 1 H sin 37 7 O 0 H sin 37 7 m m m m d . m m d . m m x x i i n i i C + + + + = = =

*3 -9质心质心运动定律 例2 求半径为R的匀质半薄球壳的质心. 解:在半球壳上取 一圆环,其质量 Rsin 0 dm o ds RdO =o2元R2sin0d0 Rcos 0 由于球壳关于y轴 x 对称,故XC=7c=0 e-dJan-∫Rcos6-o2e2sm8a0 o2πR2 ye 0-zR R 元= 2
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 例2 求半径为 R 的匀质半薄球壳的质心. 解: 在半球壳上取 一圆环, 其质量 dm = dS 2π sin d 2 = R 由于球壳关于 y 轴 对称,故 xC = zC = 0 R R 2 1 2 cos sin d π 0 = = y C j R r C 2 = 2 2 2π cos 2π sin d d 1 R R R y m m' y C = = Rsin θ x y O z θ dθ Rdθ Rcos θ R
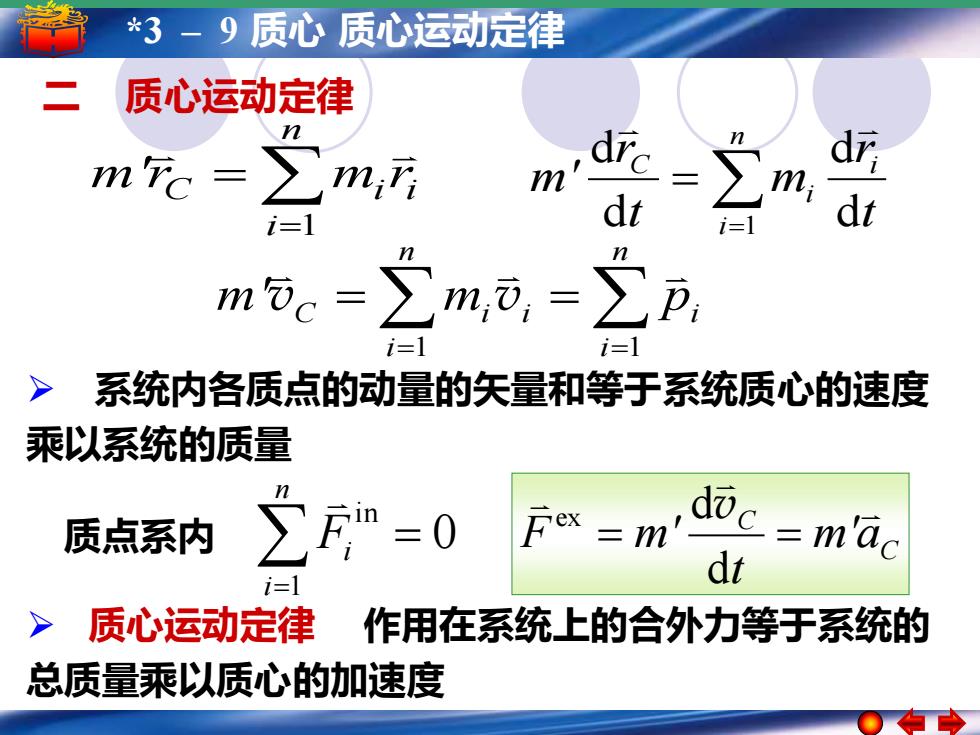
3-9质心质心运动定律 二 质心运动定律 m d i- dt mi m元e=∑m,,=∑ =1 > 系统内各质点的动量的矢量和等于系统质心的速度 乘以系统的质量 质点系内 Fin =0 Fex =m' uc=m'ac i=1 dt > 质心运动定律 作用在系统上的合外力等于系统的 总质量乘以质心的加速度
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 二 质心运动定律 i n i C i m'r m r = = 1 t r m t r m' i n i i C d d d d 1 = = = = = = n i i i n i m ' C mi p 1 1 v v C C m'a t F m' = = d ex dv 0 1 in = = n i Fi 质点系内 ➢ 质心运动定律 作用在系统上的合外力等于系统的 总质量乘以质心的加速度 ➢ 系统内各质点的动量的矢量和等于系统质心的速度 乘以系统的质量
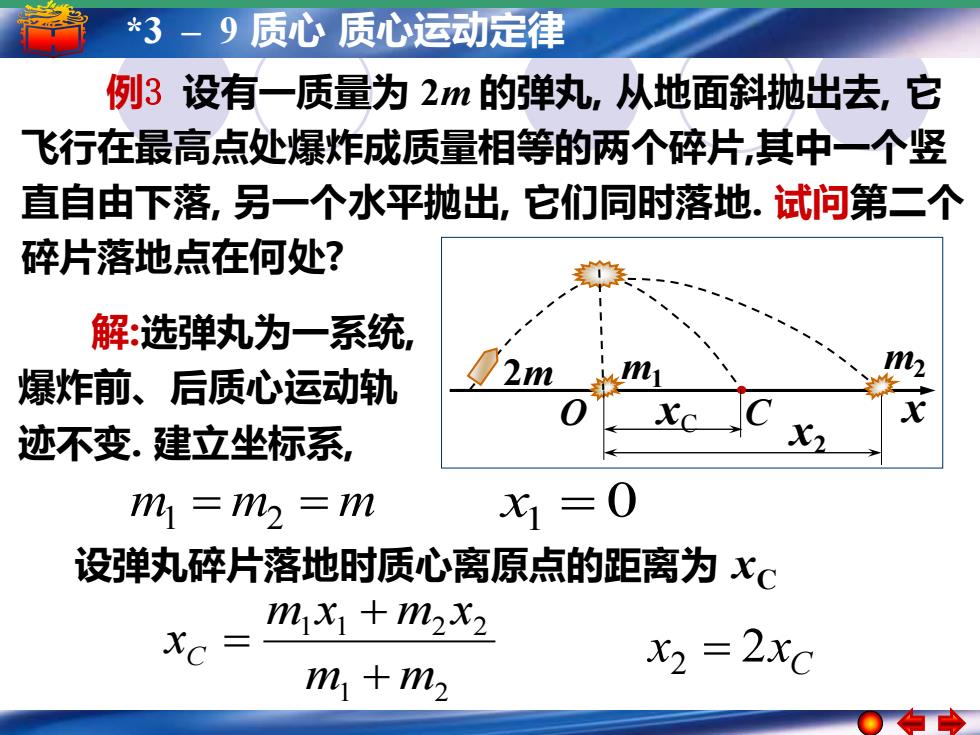
*3-9质心质心运动定律 例3设有一质量为2m的弹丸,从地面斜抛出去,它 飞行在最高点处爆炸成质量相等的两个碎片,其中一个竖 直自由下落,另一个水平抛出,它们同时落地.试问第二个 碎片落地点在何处? 解:选弹丸为一系统, 爆炸前、后质心运动轨 2 迹不变.建立坐标系, m=m=m x1=0 设弹丸碎片落地时质心离原点的距离为x℃ mx+mx2 X2 =2XC m1+m2
5 *3 – 1 简谐运动 – 9 质心简谐运动的振幅 质心运动定律周期 频率和相位 例3 设有一质量为 2m 的弹丸, 从地面斜抛出去, 它 飞行在最高点处爆炸成质量相等的两个碎片,其中一个竖 直自由下落, 另一个水平抛出, 它们同时落地. 试问第二个 碎片落地点在何处? 解:选弹丸为一系统, 爆炸前、后质心运动轨 迹不变. 建立坐标系, 设弹丸碎片落地时质心离原点的距离为 xC 1 2 1 1 2 2 m m m x m x xC + + = C x 2x 2 = O xC C x2 2m m m2 1 x m1 = m2 = m x1 = 0