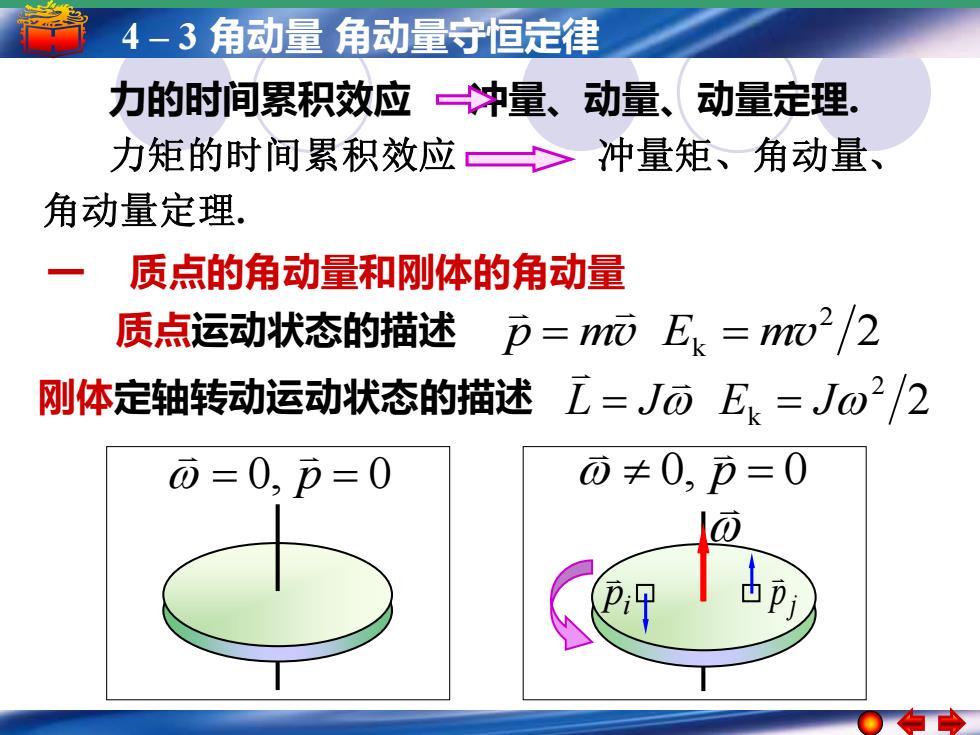
4-3角动量角动量守恒定律 力的时间累积效应钟量、动量、动量定理。 力矩的时间累积效应冲量矩、角动量、 角动量定理. 质点的角动量和刚体的角动量 质点运动状态的描述p=而 Es=w2/2 刚体定轴转动运动状态的描述工=JōE=Jw2/2 ō=0,p=0 可≠0,币=0
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 力矩的时间累积效应 冲量矩、角动量、 角动量定理. i p j p 0, p = 0 一 质点的角动量和刚体的角动量 2 2 p = mv Ek = mv 质点运动状态的描述 力的时间累积效应 冲量、动量、动量定理. 2 2 L = J Ek = J 刚体定轴转动运动状态的描述 = 0, p = 0

4-3角动量角动量守恒定律 一质点的角动量和刚体的角动量 1 质点角动量 质点在垂直于z轴平面 上以角速度作半径为r 的圆运动. > 质点角动量(相对圆心)/日=90 i=F×p=F×m0 大小L=m)sinO 1) L=m)=mr20(圆运动) 工的方向符合右手法则
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 一 质点的角动量和刚体的角动量 v L = r p = r m 质点在垂直于 z 轴平面 上以角速度 作半径为 r 的圆运动. 大小 L = rmvsin L 的方向符合右手法则. r z v O m = 90 1 质点角动量 ➢ 质点角动量(相对圆心) A mv r L z 2 L = rmv = mr (圆运动)

4-3角动量角动量守恒定律 2 刚体定轴转动的角动量 L=∑m0,=(∑m,52)w Z L=Jω 二刚体定轴转动的角动量定理 M-. L d(Jo) dt dt =dl=Jo,-J® 非刚体定轴转动的角动量定理 [Mdt-J:@2-Jo
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 2 刚体定轴转动的角动量 = = i i i i i i i L m r ( m r ) 2 v 二 刚体定轴转动的角动量定理 2 1 2 1 2 1 Mdt dL J J L L t t = = − 非刚体定轴转动的角动量定理 2 2 1 1 2 1 Mdt J J t t = − O i r mi i v t J t L M d d( ) d d = = L = J z

4-3角动量角动量守恒定律 > 刚体定轴转动的角动量定理 Mdt =Jo,-J@ 三 刚体定轴转动的角动量守恒定律 若M=,则 L=Jo=常量 讨论 守恒条件M=0 若不变,不变;若变,也变,但 不变和 > 内力矩不改变系统的角动量。 > 在冲击等问题中·.:Mm>Mx∴.L≈常量 > 角动量守恒定律是自然界的一个基本定律
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 ➢ 角动量守恒定律是自然界的一个基本定律. ➢ 内力矩不改变系统的角动量. ➢ 守恒条件 M = 0 若 J 不变, 不变;若 变, J 也变,但 L 不变 = J . ➢ 刚体定轴转动的角动量定理 2 1 2 1 Mdt J J t t = − ➢ 若 M = ,则 0 L = J = 常量. 讨论 in ex ➢ 在冲击等问题中 M M L 常量 三 刚体定轴转动的角动量守恒定律
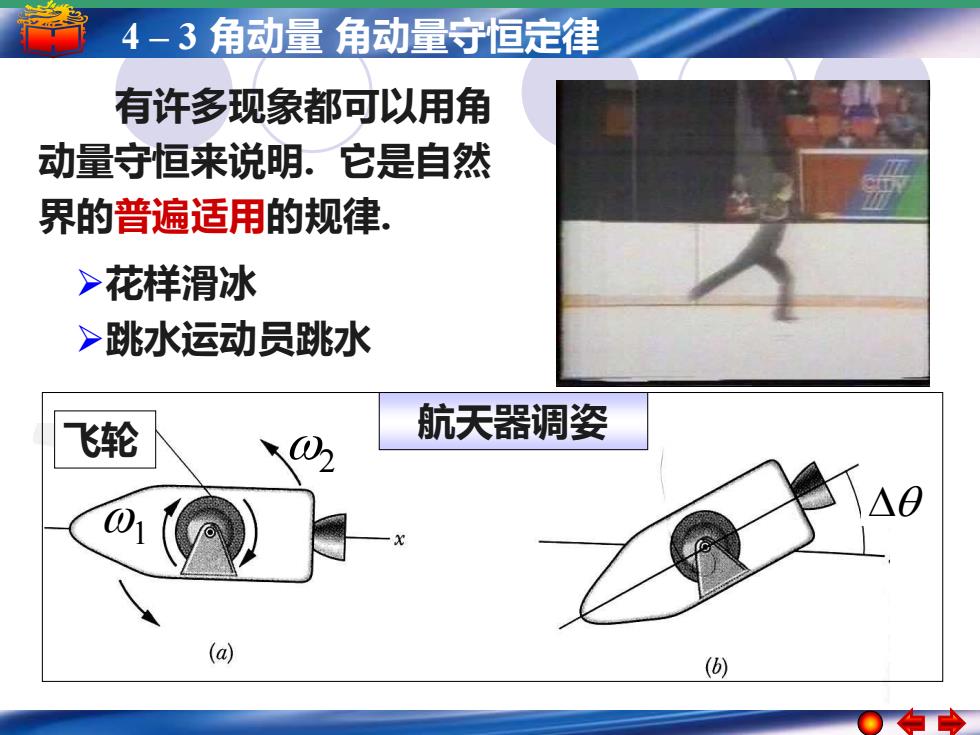
4-3角动量角动量守恒定律 有许多现象都可以用角 动量守恒来说明。它是自然 界的普遍适用的规律。 >花样滑冰 >跳水运动员跳水 飞轮 航天器调姿 0 (a) ()
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 有许多现象都可以用角 动量守恒来说明. 它是自然 界的普遍适用的规律. ➢花样滑冰 ➢跳水运动员跳水 飞轮 1 2 航天器调姿

4-3角动量角动量守恒定律 例1两个转动惯量分别为J1和J,的圆盘A和B.A 是机器上的飞轮,B是用以改变飞轮转速的离合器圆盘。 开始时,他们分别以角速度0,和2绕水平轴转动.然后, 两圆盘在沿水平轴方向力的作用下,啮合为一体,其角速 度为0,求: 齿轮啮合后两圆盘的角速度, 解:系统角动量守恒 J10+J202=(J1+J2)w J101+J202 0= (J+J2) +IB
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 解: 系统角动量守恒 J1 1 + J2 2 = (J1 + J2 ) ( ) 1 2 1 1 2 2 J J J J + + = 例1 两个转动惯量分别为 J1 和 J2 的圆盘 A和 B. A 是机器上的飞轮,B 是用以改变飞轮转速的离合器圆盘. 开始时,他们分别以角速度1 和2 绕水平轴转动.然后, 两圆盘在沿水平轴方向力的作用下,啮合为一体, 其角速 度为,求: 齿轮啮合后两圆盘的角速度

4-3角动量角动量守恒定律 例2一杂技演员M由距水平跷板高为h处自由下 落到跷板的一端A,并把跷板另一端的演员W弹了起来. 设跷板是匀质的,长度为1,质量为跷板可绕中部支撑 点C在竖直平面内转动,演员的质量均为m.假定演员M 落在跷板上,与跷板的碰撞是完全非弹性碰撞.问演员N 可弹起多高? 解:碰撞前M落在A 点的速度 0M=(2gh)2 碰撞后的瞬间,M 2 具有相同的线速度
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 解:碰撞前 M 落在 A 点的速度 1 2 v M = (2gh) 例2 一杂技演员 M 由距水平跷板高为 h 处自由下 落到跷板的一端 A, 并把跷板另一端的演员 N 弹了起来. 设跷板是匀质的,长度为 l ,质量为 ,跷板可绕中部支撑 点 C 在竖直平面内转动,演员的质量均为 m.假定演员 M 落在跷板上,与跷板的碰撞是完全非弹性碰撞 .问演员 N 可弹起多高 ? m' l l/2 C A B M N h 碰撞后的瞬间, M、N 具有相同的线速度
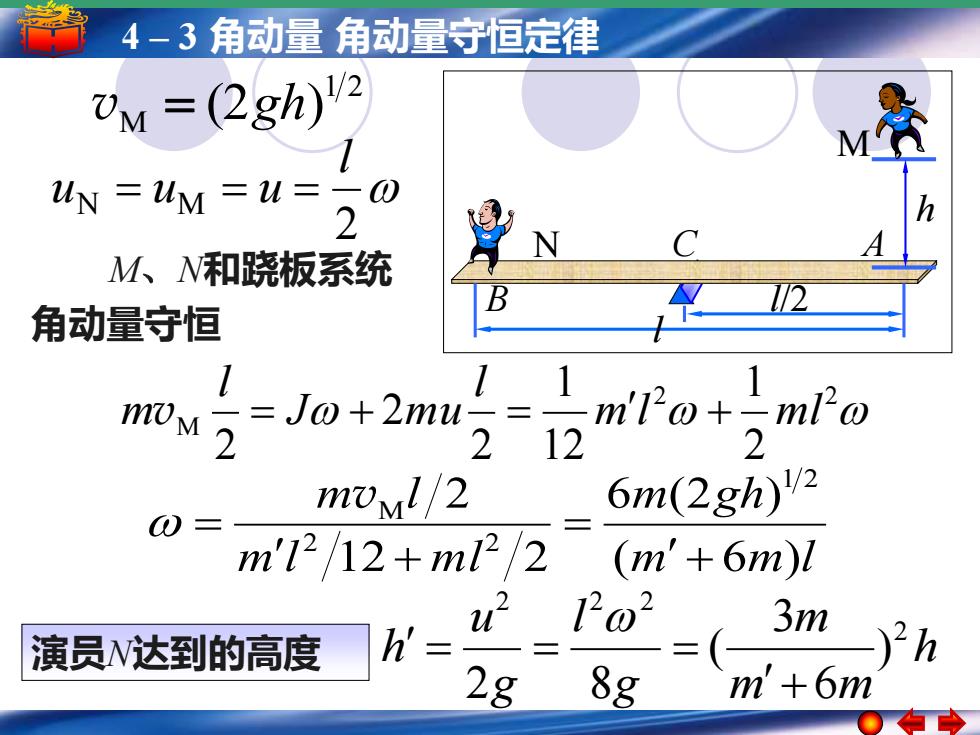
4-3角动量角动量守恒定律 M=(2gh)'2 4=M=M=20 h M、W和跷板系统 角动量守恒 12 11 10M2=J0+2mu言 mFo+-mFo 212 2 moml/2 6m(2gh)'2 m'12/12+m12/2 (m'+6m)l u212o2 3m 演员W达到的高度 h'= )2h 2g 8g m'+6m
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 M、N和跷板系统 角动量守恒 1 2 v M = (2gh) 2 N M l u = u = u = 2 2 M 2 1 12 1 2 2 2 m l m l l J m u l mv = + = + m m l m gh m l m l m l ( 6 ) 6 (2 ) 12 2 2 1 2 2 2 M + = + = v 演员N达到的高度 h m m m g l g u h 2 2 2 2 ) 6 3 ( 2 8 + = = = l l/2 C A B M N h

4-3角动量角动量守恒定律 例3质量很小长度为1的均匀细杆,可绕过其中心O 并与纸面垂直的轴在竖直平面内转动.当细杆静止于水平 位置时,有一只小虫以速率垂直落在距点O为4处, 并背离点O向细杆的端点A爬行.设小虫与细杆的质量均 为m.问欲使细杆以恒定的角速度转动,小虫应以多大速率 向细杆端点爬行? 解碰撞前后系统角动 量守恒 71 m,4[btm好e 0=1200/71
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 例3 质量很小长度为l 的均匀细杆,可绕过其中心 O 并与纸面垂直的轴在竖直平面内转动.当细杆静止于水平 位置时,有一只小虫以速率 垂直落在距点 O 为 l/4 处, 并背离点O 向细杆的端点 A 爬行.设小虫与细杆的质量均 为m.问:欲使细杆以恒定的角速度转动,小虫应以多大速率 向细杆端点爬行? 0 v 解:碰撞前后系统角动 量守恒 = + 2 2 0 ) 4 ( 12 1 4 l ml m l mv 12 7l = v0
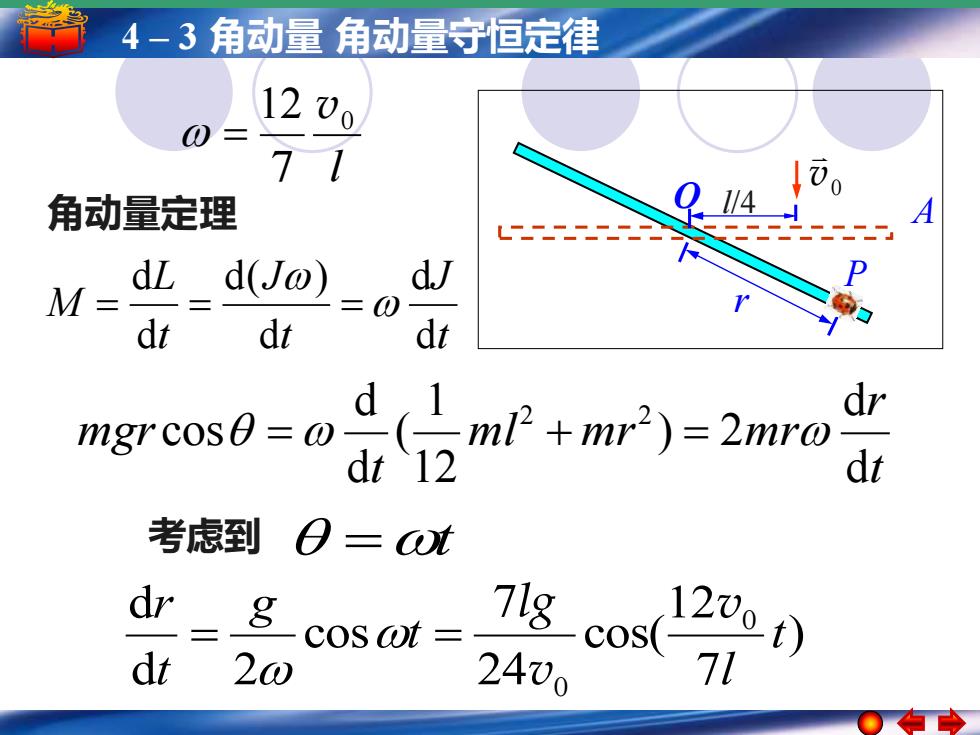
4-3角动量角动量守恒定律 1200 71 角动量定理 4 dl d(Jo) dJ M= dt dt dt d mgrcos0 w (ml+mr2)=2mro dr dt 12 dr 考虑到O=)t dr cos at 120ot) dt 20 18co 2400
5 4 – –1 简谐运动 3 角动量简谐运动的振幅 角动量守恒定律周期 频率和相位 l 0 7 12 v = 角动量定理 t J t J t L M d d d d( ) d d = = = t r m l m r m r t mgr d d ) 2 12 1 ( d d cos 2 2 = + = 考虑到 =t ) 7 12 cos( 24 7 cos d 2 d 0 0 t l t g t r v v lg = = O l/4 0 v A r P