机械振动习题课选讲例题 例图中所画的是两个简谐振动的振动曲线。若这两 个简谐振动可叠加,则合成的余弦振动的初相为 (A)3元/2 大(B)元 A/2 (C)π/2 (D)零
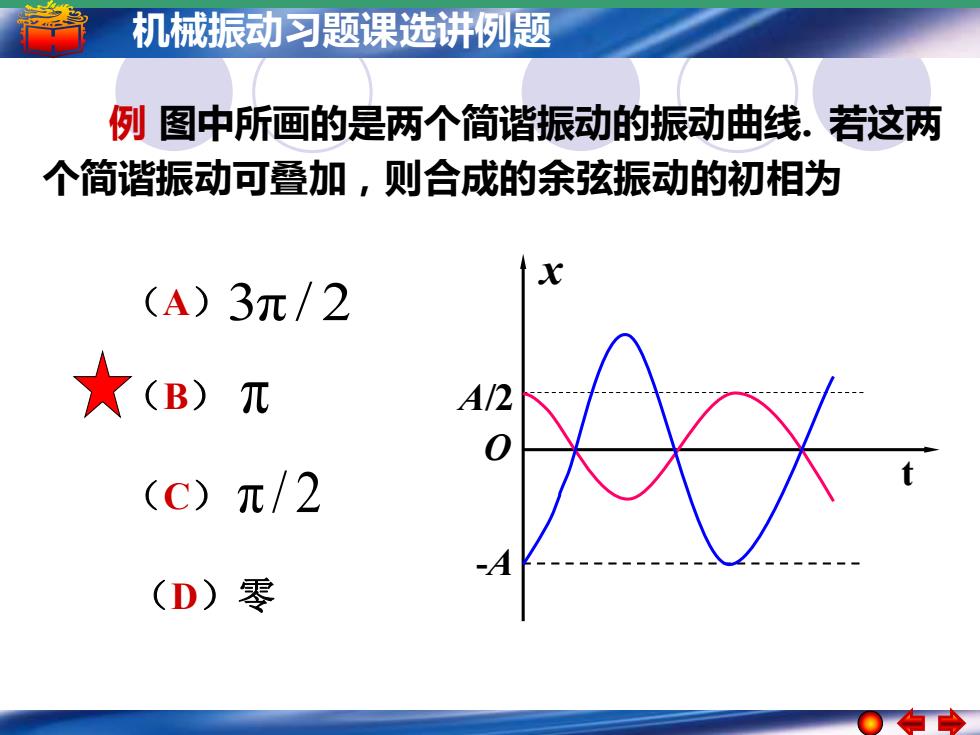
机械振动习题课选讲例题 例 图中所画的是两个简谐振动的振动曲线. 若这两 个简谐振动可叠加,则合成的余弦振动的初相为 A/2 -A O x t (A) (B) 3π / 2 (D)零 π (C) π / 2
机械振动习题课选讲例题 例一质点作谐振动,周期为T,当它由平衡位置向 X轴正方向运动时,从二分之一最大位移处到最大位 移处这段路程所需要的时间为 (A)T/4 (B)T/12 ★ (C)T6 (D)T/8 △p π/3 △t 2元 2元 T △t=T/6
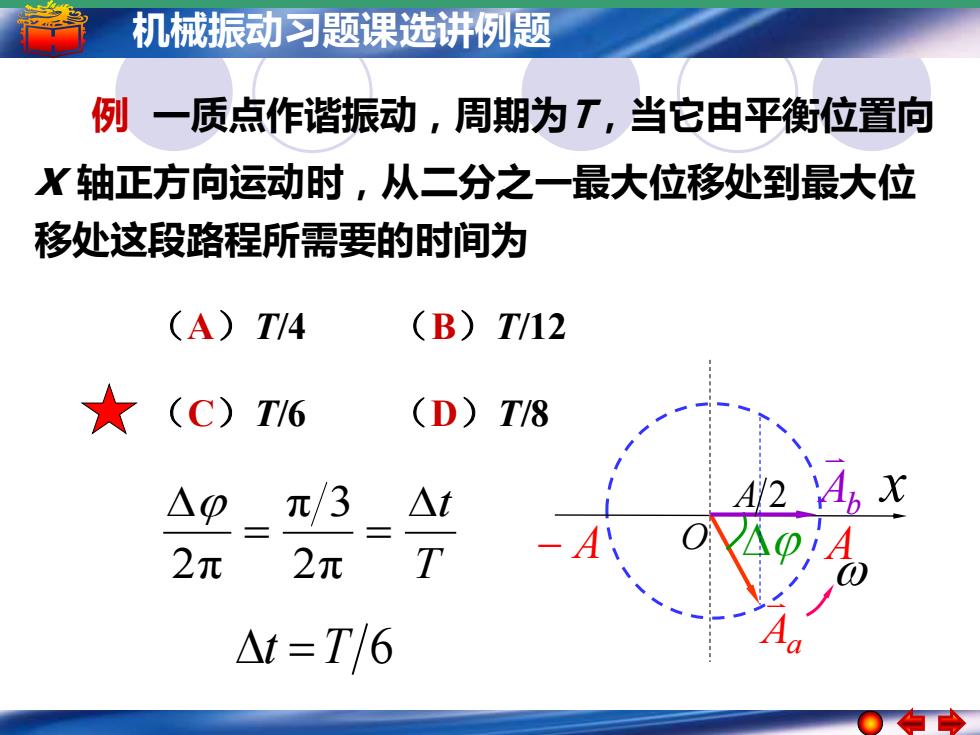
机械振动习题课选讲例题 例 一质点作谐振动,周期为T,当它由平衡位置向 x 轴正方向运动时,从二分之一最大位移处到最大位 移处这段路程所需要的时间为 (A)T/4 (B)T/12 (C)T/6 (D)T/8 T t = = 2π π 3 2π t =T 6 x − A O A Aa Ab A 2

机械振动习题课选讲例题 例已知一谐振动曲线如图所示,由图确定: (1)在+1/2s时速度为零(2)在ks时动能最大 (3)在2k+1/2s时加速度取正的最大值 x/cm tis
机械振动习题课选讲例题 例 已知一谐振动曲线如图所示,由图确定: (1)在_s时速度为零 (2)在_s时动能最大 (3)在_s时加速度取正的最大值 k+1/2 k 2k+1/2 O x/cm 1 2 t/s
机械振动习题课选讲例题 例用旋转矢量法求初相位 x=Acos(ot+o) Mi t=0x=0)<0 A 元
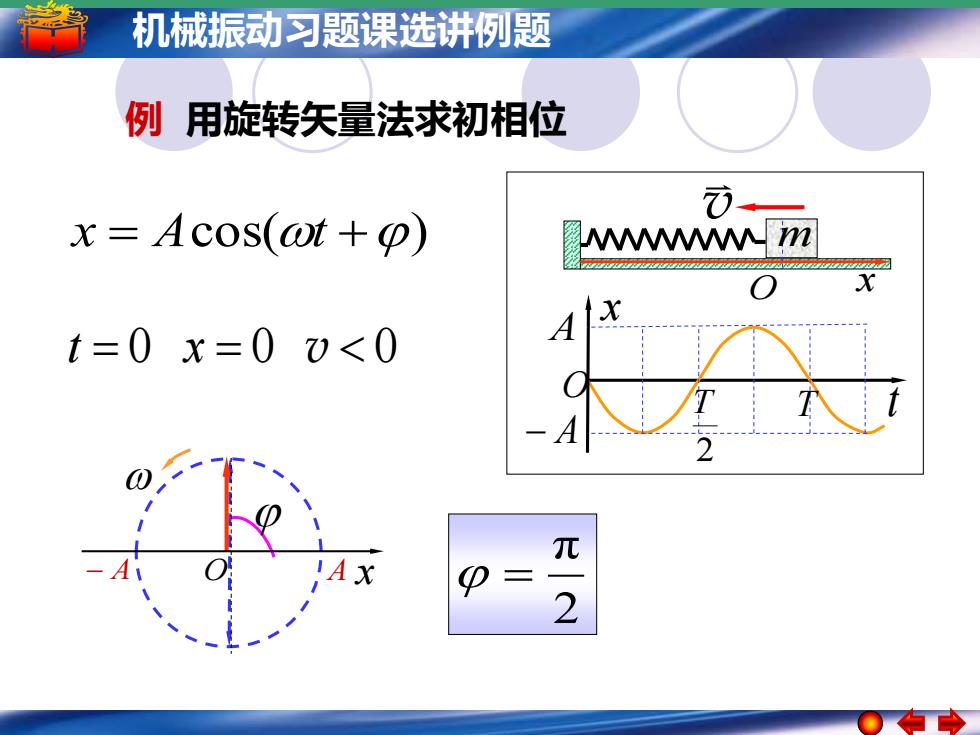
机械振动习题课选讲例题 x = Acos(t +) t = 0 x = 0 v 0 2 π − A O A x = v m O x O A − A x 2 T T t 例 用旋转矢量法求初相位
机械振动习题课选讲例题 例 一简谐运动的运 动曲线如图所示,求振动 周期 A t=0 X= )0 △币=5元/6 A x △中 _△t7.5 2元 T T t=7.5s T=18S
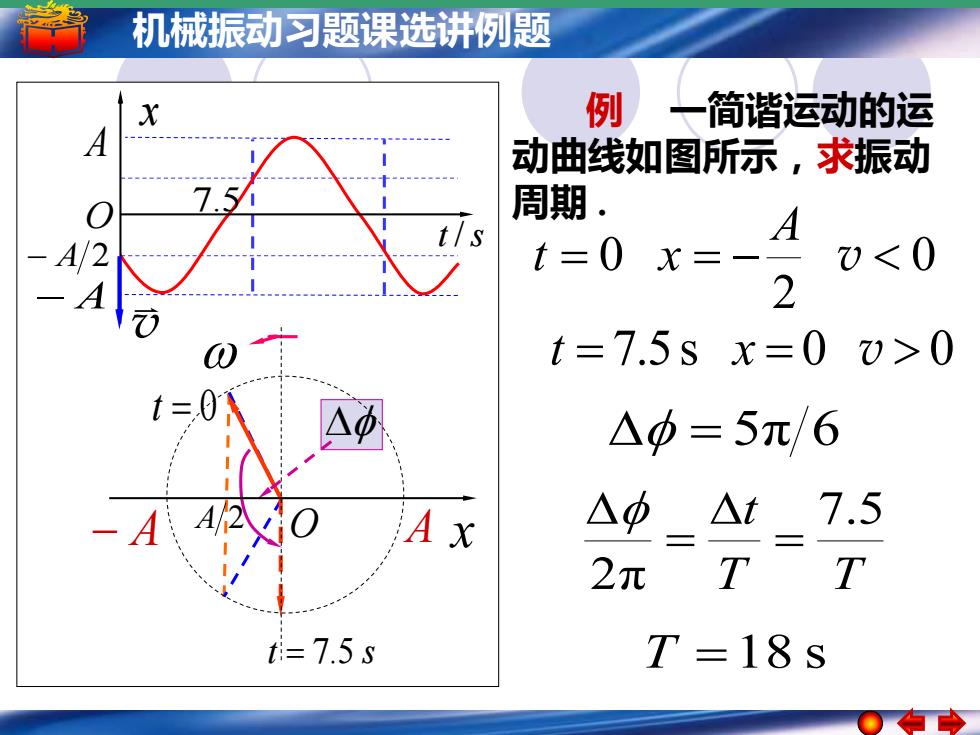
机械振动习题课选讲例题 A 2 例 一简谐运动的运 动曲线如图所示,求振动 周期 . 0 2 = 0 = − v A t x t = 0 t = 7.5 s x = 0 v 0 = 5π 6 T T t 7.5 2π = = t = 7.5 s T =18 s 0 A x t /s − A 2 O − A v 7.5 − A O A x

机械振动习题课选讲例题 例 已知谐振动的A、T,求(1)如图简谐运动 方程,(2)到达a、b点运动状态的时间 解法一 0A x=Acos(ot+o) A/2 从图上可知 A t=0,x= 0>0 2 A 0=± 或3 元5元 2 1 ·o>0,inp <0 coso 2 元 5元 .0= 或 x=AcOS(ωt- 3 3
机械振动习题课选讲例题 O A − A x A 2 * * a b t 例 已知谐振动的 A 、T ,求 (1)如图简谐运动 方程, (2)到达 a、b 点运动状态的时间 . x = Acos(t +) 解法一 从图上可知 , 0 2 = 0, = v A t x cos 2 A A = 2 1 cos = ) 3 5π , 3 π ( 3 π = 或 v0 0,sin 0 3 5π 3 π = − 或 ) 3 π x = Acos(t − v

机械振动习题课选讲例题 x=Acos(ot- 3 A=Ac0s(ot。-π/3) %-号=-02z4元 A =Ac0s(Dtb-π/3) (,-p<2元 2 π元5π7π. 2,- =0 333’3 T a 3 T-6 %-<2a2- T b=T/3
机械振动习题课选讲例题 ) 3 π x = Acos(t − = cos( − π 3) a A A t 0,2π,4π, 3 π t a − = ) 2π 3 π (t a − − 0 3 2π π t a − = T 6 T t a = cos( π 3) 2 = A t b − A 3 7π , 3 5π , 3 π 3 π t b − = ) 2π 3 π (t b − − 3 π 3 2π π t b − = T t b = T 3 O A − A x A 2 * * a b v t

机械振动习题课选讲例题 解法二 用旋转矢量法求初相位 x=Acos(at+o) A t= 0,x= ,0>0 2 矢量位于轴下方时 )>0 元 3 =Acos(aut-) 3
机械振动习题课选讲例题 解法二 x = Acos(t +) A/2 , 0 2 = 0, = v A t x 3 π = − x − A O A 矢量位于 x 轴下方时 v 0 O A − A x A 2 * * a b v t 用旋转矢量法求初相位 A/2 ) 3 π x = Acos(t −

机械振动习题课选讲例题 th A/2 t=0 x =Acos(ot- 39 2元 A0=0-(-3 元 3 3 △T= T t6= △中T= T ta 2元 6 2元 3
机械振动习题课选讲例题 t = 0 − A O A x A/2 2π 6 T t a T = = a t = t 3 π ) 3 π = 0 − (− = O A − A x A 2 * * a b v t ) 3 π x = Acos(t − b t = t 3 2π ) 3 π ( 3 π = − − = 2π 3 T t b T = =

机械振动习题课选讲例题 例 求两个同方向同频率的简谐振动的合振幅 x1=(3×102m)cos(ot-π/6) x2=(4×102m)cos(ot+元/3) ap=:-0-9-(爱- 2 A=42+42+244 cos(2-) A=4+4 =5×102m
机械振动习题课选讲例题 例 求两个同方向同频率的简谐振动的合振幅 (3 10 m)cos( π 6) 2 1 = − − x t (4 10 m)cos( π 3) 2 2 = + − x t 2 π ) 6 π ( 3 π =2 −1 = − − = A 2 2 2 A = A1 + A 5 10 m −2 = O x A1 A2 1 2 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A −