
5-3简谐运动的能量 以弹簧振子为例 Ac0s(o1+0 v=-Aosin(ot+p) 1 2 1 mo2Asin2(at+o) 2 2 1 E 2=二k2cos2(ot+p) 2 02 =k/m E=E+E。=二kPcA(振幅的动力学意义) 线性恢复力是保守力,做简谐运动的系统机械能守恒
5 – 3 简谐运动的能量 sin ( ) 2 1 2 1 2 2 2 2 Ek = mv = m A t + cos ( ) 2 1 2 1 2 2 2 Ep = k x = k A t + 线性恢复力是保守力,做简谐运动的系统机械能守恒 以弹簧振子为例 sin( ) cos( ) = − + = + A t x A t v F = −kx 2 2 k p 2 1 E = E + E = k A A k / m 2 = (振幅的动力学意义)
5-3简谐运动的能量 简谐运动能量图 X,0 0=0 x=Acosot -t v=-Aosin ot 能量 E= 4 2 kA cos2 wt 2 3江T -mo2A2 sin2 ot 4
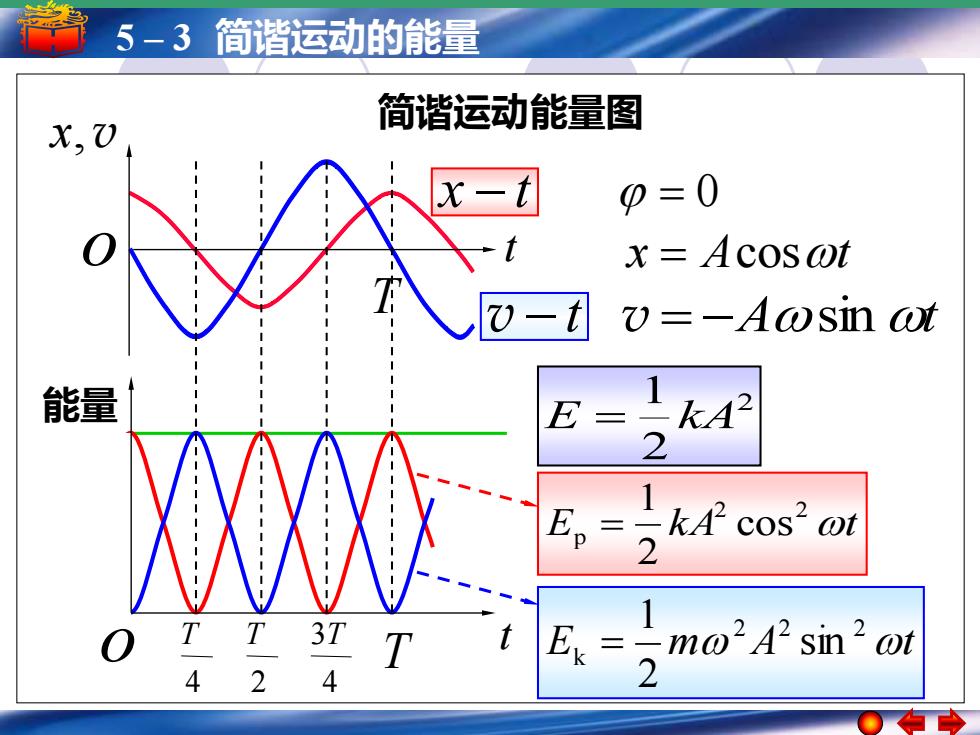
5 – 3 简谐运动的能量 简谐运动能量图 x − t v − t 2 2 1 E = kA = 0 x = Acost v = −Asint x, v o t T 4 T 2 T 4 3T 能量 o T t E k A t 2 2 p cos 2 1 = E m A t 2 2 2 k sin 2 1 =

5-3简谐运动的能量 例质量为0.10kg的物体,以振幅1.0×102m 作简谐运动,其最大加速度为4.0ms2,求:(1) 振动的周期;(2)通过平衡位置的动能;(3)总能量; (4)物体在何处其动能和势能相等? 解(1) =A02 2元 0 =20s T= =0.314s A 0 (2)通过平衡位置的动能; 1 Ek.mx 2 -mv 1 2 max mo2A2=2.0×10-3J 2
5 – 3 简谐运动的能量 例 质量为 0.10 kg 的物体,以振幅1.0×10 -2 m 作简谐运动,其最大加速度为 4.0 m·s -2 , 求:(1) 振动的周期;(2)通过平衡位置的动能;(3)总能量; (4)物体在何处其动能和势能相等? (2)通过平衡位置的动能; 解 (1) 2 amax = A A amax = 1 20 s − = 0.314 s 2 π = = T 2.0 10 J −3 = 2 2 2 k,max max 2 1 2 1 E = mv = m A

5-3简谐运动的能量 T=0.314s =2.0×103J (3)总能量; E=Ek.mx =2.0×10-3J (4)物体在何处其动能和势能相等? Ek=E。时, E=1.0×103J 2Ep =0.5×104m2x=±0.707cm mw
5 – 3 简谐运动的能量 E = Ek,max 2.0 10 J −3 = Ek = Ep 时, 1.0 10 J 3 p − E = 由 2 2 2 p 2 1 2 1 E = k x = m x 2 2 p 2 m E x = 4 2 0.5 10 m − = x = 0.707 cm (3)总能量; (4)物体在何处其动能和势能相等? 2.0 10 J 3 k,max − T = 0.314 s E =