《大学物理》课程教学课件（PPT讲稿，高教版）2-4 牛顿定律的应用举例

2-4 牛顿定律应用举例 解题的基本思路 (1)确定研究对象进行受力分析； (隔离物体，画受力图，不要画力的分解图.) (2)取坐标系； (3)列方程（一般用分量式，用文字符号列方程式）； (④)利用其他的约束条件列补充方程； (⑤)先用文字符号求解，后代入数据计算结果

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 (1)确定研究对象进行受力分析； （隔离物体，画受力图，不要画力的分解图.） (2)取坐标系； (3)列方程（一般用分量式, 用文字符号列方程式）； (4)利用其他的约束条件列补充方程； (5)先用文字符号求解，后代入数据计算结果. 解题的基本思路

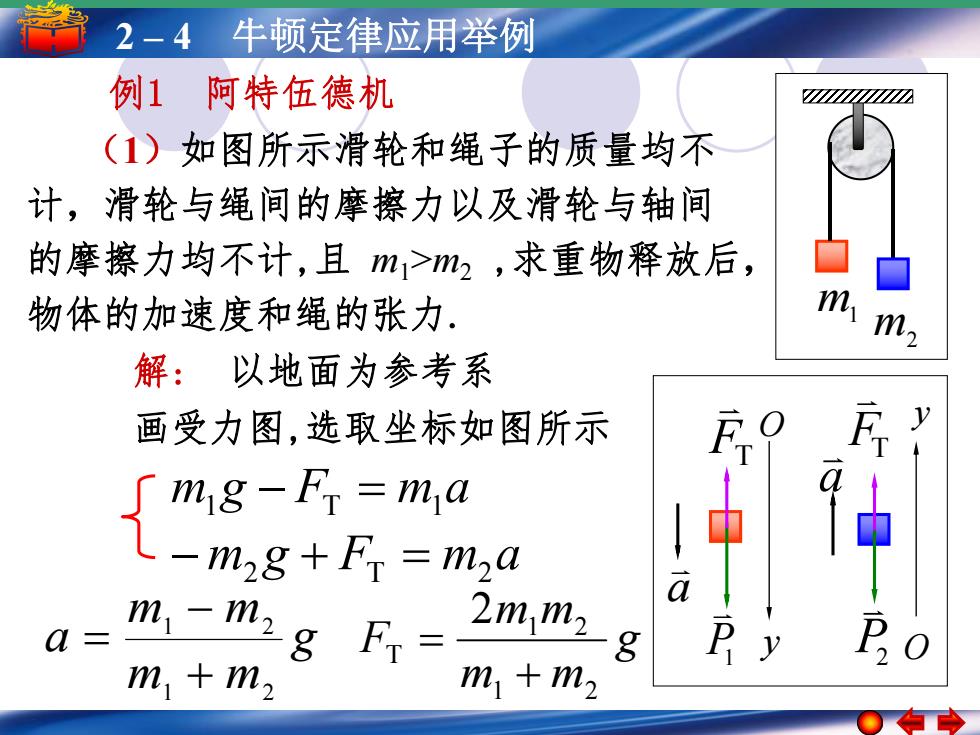
2-4牛顿定律应用举例 例1阿特伍德机 n☑ (1)如图所示滑轮和绳子的质量均不 计，滑轮与绳间的摩擦力以及滑轮与轴间 的摩擦力均不计，且m1>m2,求重物释放后， 物体的加速度和绳的张力. m m2 解：以地面为参考系 画受力图，选取坐标如图所示 F { a mm2g Fr= a ☑= 2m m2 m1+m2 m1+m2

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 P1 FT （1）如图所示滑轮和绳子的质量均不 计，滑轮与绳间的摩擦力以及滑轮与轴间 的摩擦力均不计,且 m1>m2 ,求重物释放后， 物体的加速度和绳的张力. m1 m2 m1g  FT  m1a  m2 g  FT  m2a g m m m m a 1 2 1 2    g m m m m F 1 2 1 2 T 2   解: 以地面为参考系 画受力图,选取坐标如图所示 FTP2 a  y O a  y O 例1 阿特伍德机

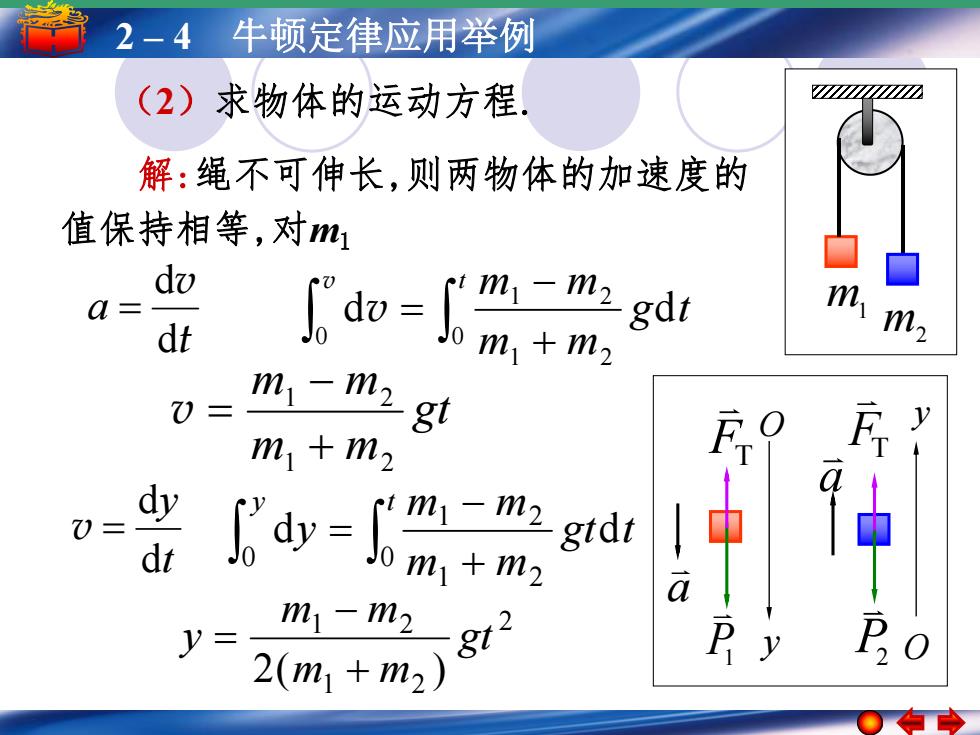
2-4 牛顿定律应用举例 (2)求物体的运动方程， a1nmm 解：绳不可伸长，则两物体的加速度的 值保持相等，对m1 dv a= m dt m, m1-m2 gt y m1+m2 0= dt 了=%0n a m1-m2 y 8t2 2(m1+m2) P y

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 （2）求物体的运动方程. m1 m2 gt m m m m 1 2 1 2   v  解:绳不可伸长,则两物体的加速度的 值保持相等,对m1 t v d d a       t g t m m m m 0 1 2 1 2 0 d d v v t y d d v       y t gt t m m m m y 0 1 2 1 2 0 d d 2 1 2 1 2 2( ) gt m m m m y    P1 FT FTP2 a  y O a  y O

2-4牛顿定律应用举例 (3)若将此装置置于电梯顶部，当 电梯以加速度ā相对地面向上运动时， a 求两物体相对电梯的加速度和绳的张力. a. 解：以地面为参考系 设两物体相对于地面的加速度分别 m m2 为a、d2,且相对电梯的加速度为a m8-F=m,41 0 m-m2(g+a) a, a=a.-a m1+m2 mag+F=mdzF= 2mm(g+a) a a,=a,+a +m

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 P1 FT （3）若将此装置置于电梯顶部，当 电梯以加速度 相对地面向上运动时， 求两物体相对电梯的加速度和绳的张力. a  m1 m2 a  r a  r a  解:以地面为参考系 设两物体相对于地面的加速度分别 为 a 1 、 ，且相对电梯的加速度为  ar  2 a  FTP2 a1   y O a2 y O m1g  FT  m1a1 2 T 2 2 m g  F  m a a  a  a 1 r a2  ar  a ( ) 1 2 1 2 r g a m m m m a     ( ) 2 1 2 1 2 T g a m m m m F   

2-4 牛顿定律应用举例 例2设有一质量为m=2500kg的汽车，在平直的高 速公路上以每小时120km的速度行驶.若欲使汽车平稳 地停下来，驾驶员启动刹车装置，刹车阻力是随时间线性 增加的，即F=-bt,其中b=3500Ns1.试问此车经过 多长时间停下来 bt 解：汽车的加速度 a=- m dv dt ∫do=∫adr rdo=(-b)d 1=(202m)2=6.90s 思考：在6.90s的时间里，汽车行进了多长的路程？

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 ) 6.90 s 2 ( 1 2  m  b t v0 t v d d a      t bt t m 0 ( )d 1 d 0 v0 v   dv  adt 解: 汽车的加速度 m bt a   思考:在 6.90 s 的时间里,汽车行进了多长的路程 ? 例2 设有一质量为m = 2 500 kg 的汽车,在平直的高 速公路上以每小时120 km 的速度行驶.若欲使汽车平稳 地停下来,驾驶员启动刹车装置,刹车阻力是随时间线性 增加的,即 Ff =  bt ,其中 b = 3 500 N·s -1 . 试问此车经过 多长时间停下来

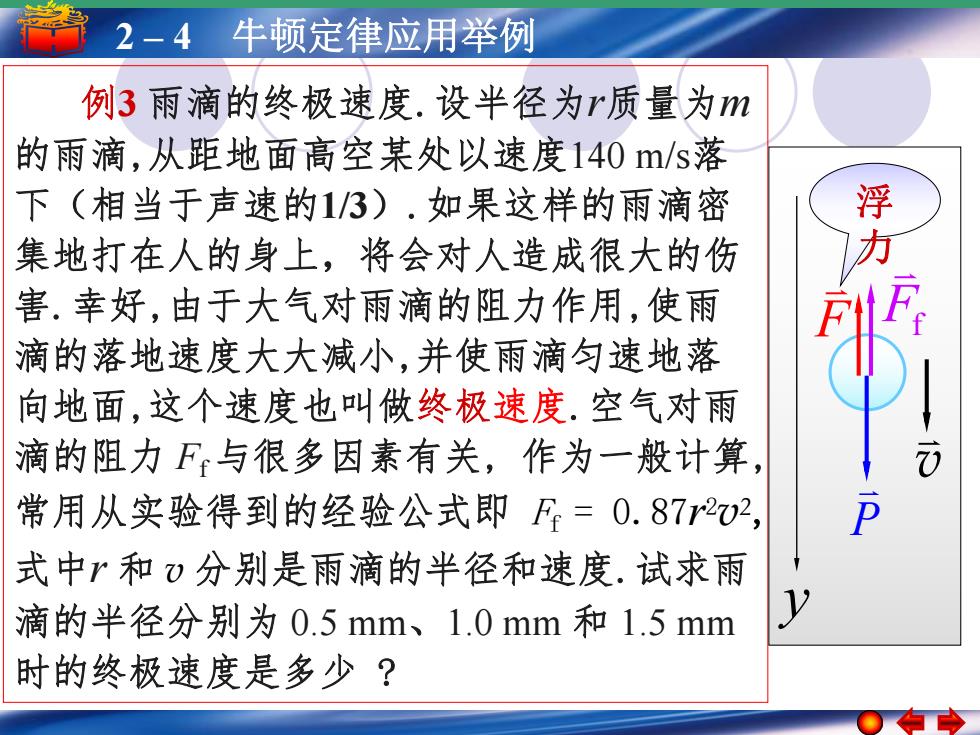
2-4牛顿定律应用举例 例3雨滴的终极速度.设半径为r质量为m 的雨滴，从距地面高空某处以速度140m/s落 下（相当于声速的13）.如果这样的雨滴密 浮 集地打在人的身上，将会对人造成很大的伤 害.幸好，由于大气对雨滴的阻力作用，使雨 F 滴的落地速度大大减小，并使雨滴匀速地落 向地面，这个速度也叫做终极速度.空气对雨 滴的阻力F与很多因素有关，作为一般计算 常用从实验得到的经验公式即F=0.872v2, 式中r和)分别是雨滴的半径和速度.试求雨 滴的半径分别为0.5mm、1.0mm和1.5mm 时的终极速度是多少？

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 例3 雨滴的终极速度.设半径为r质量为m 的雨滴,从距地面高空某处以速度140 m/s落 下（相当于声速的1/3）.如果这样的雨滴密 集地打在人的身上，将会对人造成很大的伤 害.幸好,由于大气对雨滴的阻力作用,使雨 滴的落地速度大大减小,并使雨滴匀速地落 向地面,这个速度也叫做终极速度.空气对雨 滴的阻力 Ff与很多因素有关, 作为一般计算, 常用从实验得到的经验公式即 Ff = 0.87r 2v2 , 式中r 和 v 分别是雨滴的半径和速度.试求雨 滴的半径分别为 0.5 mm、1.0 mm 和 1.5 mm 时的终极速度是多少 ? v  F  Ff  P  y 浮 力

2-4 牛顿定律应用举例 已知：F=0.87r2)2,p=103kgmp2=1.0kgm 解：雨滴的密度为P,空气的密度为P2 dv 浮 mg-F-F=m dt 4 4 rpg-于wpg-0.87r2g 3 2=m dv 3 dt r3(p1-p2)8-0.87r2)2=m do 3 dt 雨滴匀速时☑=O 4.86ms r=0.5 mm 72 6.88ms1 r=1.0 mm 8.4ms r =1.5 mm

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 t mg F F m d d f v    t r g r g r m d d π 0.87 3 4 π 3 4 2 2 2 3 1 3 v     v  t r g r m d d π ( ) 0.87 3 4 2 2 1 2 3 v     v  雨滴匀速时 a  0 1.5 mm 1.0 mm 0.5 mm 8.4 m s 6.88 m s 4.86 m s 3 0.87 4π( ) -1 -1 -1 1 2 1 2 L                      r r r r   g v v  y 浮 力Ff  F P  已知： , , . 3 3 1 10 kg m     3 2 1.0 kg m     2 2 Ff  0.87r v 解:雨滴的密度为  1 ,空气的密度为 2

2-4牛顿定律应用举例 例4高台跳水游泳池的深度.为保证跳水运动员从 10m高台跳入游泳池中的安全，规范要求水深必须在 4.50~5.50m之间.为什么要作这样的规定呢？ 解：(1)运动员自由落体入水，速度 0o=2gh =14.0 m/s (2),P水≈P人，.F+p=0 设所受组力：R=-bp10 2 b=0.5,pk=1.0×103kgm3,A=0.08m2 水中安全速度0=2.0ms；人体质量m=50kg

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 例4 高台跳水游泳池的深度.为保证跳水运动员从 10 m 高台跳入游泳池中的安全,规范要求水深必须在 4.50 ~ 5.50 m 之间.为什么要作这样的规定呢 ? 解:（1）运动员自由落体入水，速度 2 14.0 m/s v0  gh  Fr  F P  （2）  F  P  0    水  人， 2 r 2 1 设所受阻力： F   bAv 3 3 2  0.5, 1.010 kg m ,  0.08 m  b  水 A 水中安全速度 ；人体质量 . 1 2.0 m s  v   m  50 kg

2-4 牛顿定律应用举例 已知：b=0.5,p水=1.0×103kgm3,A=0.08m2 一1 0o=14.0 m/s =2.0m.s m=50 kg 令k=bpA/2 F.=-k02 dv 入水后F=m =-k2 dv k dy odt dy ) m 0 dv k dy 00 0 m y= M10 00 50 14.0 4.86m 20 2.0

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位     y y m k 0 d d 0 v v v v 4.86 m 2.0 14.0 ln 20 50  ln   v v0 k m y 2 r d d v v k t 入水后 F  m   Ff F P  2 r 令 k  bA/ 2 F   kv y 3 3 2  0.5, 1.010 kg m ,  0.08 m  已知： b  水 A 1 2.0 m s  v0 14.0 m/s v   m  50 kg dy  vdt y m k d d   v v

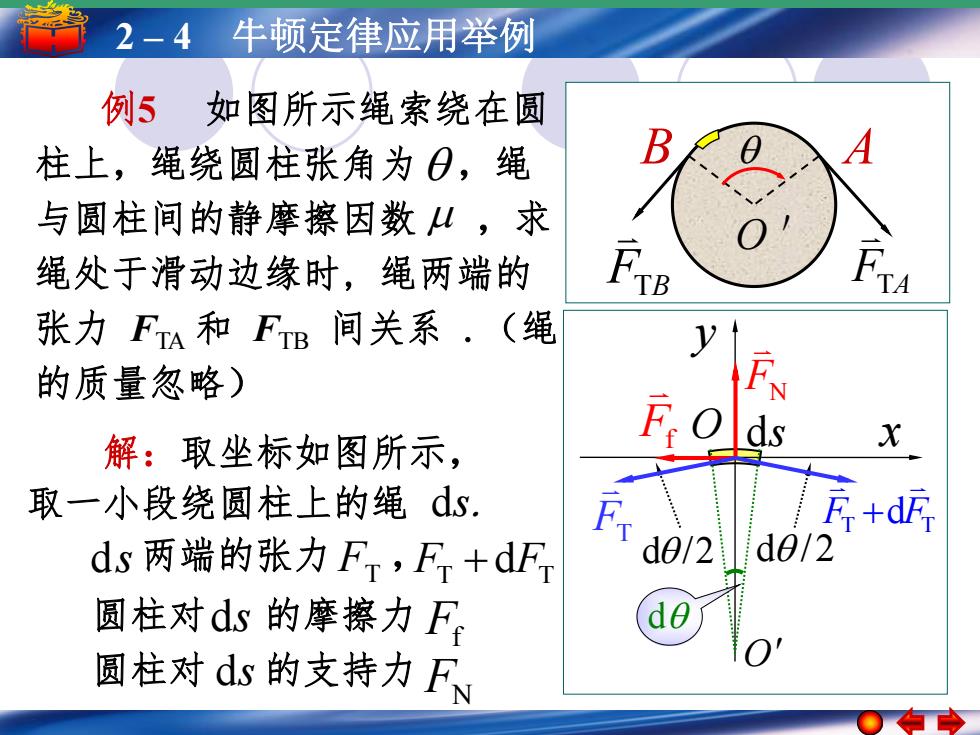
2-4牛顿定律应用举例 例5如图所示绳索绕在圆 柱上，绳绕圆柱张角为日，绳 A 与圆柱间的静摩擦因数山，求 绳处于滑动边缘时，绳两端的 TA 张力FA和FB间关系·（绳 y 的质量忽略) 解：取坐标如图所示， F:o ds X 取一小段绕圆柱上的绳ds. d ds两端的张力F,F+dF 2d0/2 圆柱对ds的摩擦力F 圆柱对ds的支持力FN

52––1 4简 谐 牛运顿动 定简律谐运应动用的举振幅例 周期 频率和相位 x y O O ds 例5 如图所示绳索绕在圆 柱上，绳绕圆柱张角为 ，绳 与圆柱间的静摩擦因数 ，求 绳处于滑动边缘时, 绳两端的 张力 FTA 和 FTB 间关系 .（绳 的质量忽略） 解：取坐标如图所示， 取一小段绕圆柱上的绳 ds.  FTA  FTB  O ＇ B A d/2 d /2 Ff  FN  FT FT dFT    圆柱对 的摩擦力 圆柱对 的支持力 Ff FN ds ds FT FT  dFT ds 两端的张力 ， d  