
1-1质点运动的描述 参考系质点 1参考系 为描述物体的运动而选择的标准物叫做参考系。 选取的参考系不同,对物体运动情况的描述不同 这就是运动描述的相对性, 坐标系:参考系的数学抽象 2质点 如果我们研究某一物体的运动,而可以忽略其 大小和形状对物体运动的影响,若不涉及物体的转 动和形变,我们就可以把物体当作一个具有质量的 点(即质点)来处理
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 一 参考系 质点 为描述物体的运动而选择的标准物叫做参考系. 1 参考系 如果我们研究某一物体的运动,而可以忽略其 大小和形状对物体运动的影响,若不涉及物体的转 动和形变,我们就可以把物体当作一个具有质量的 点(即质点)来处理 . 2 质点 选取的参考系不同,对物体运动情况的描述不同, 这就是运动描述的相对性. 坐标系:参考系的数学抽象
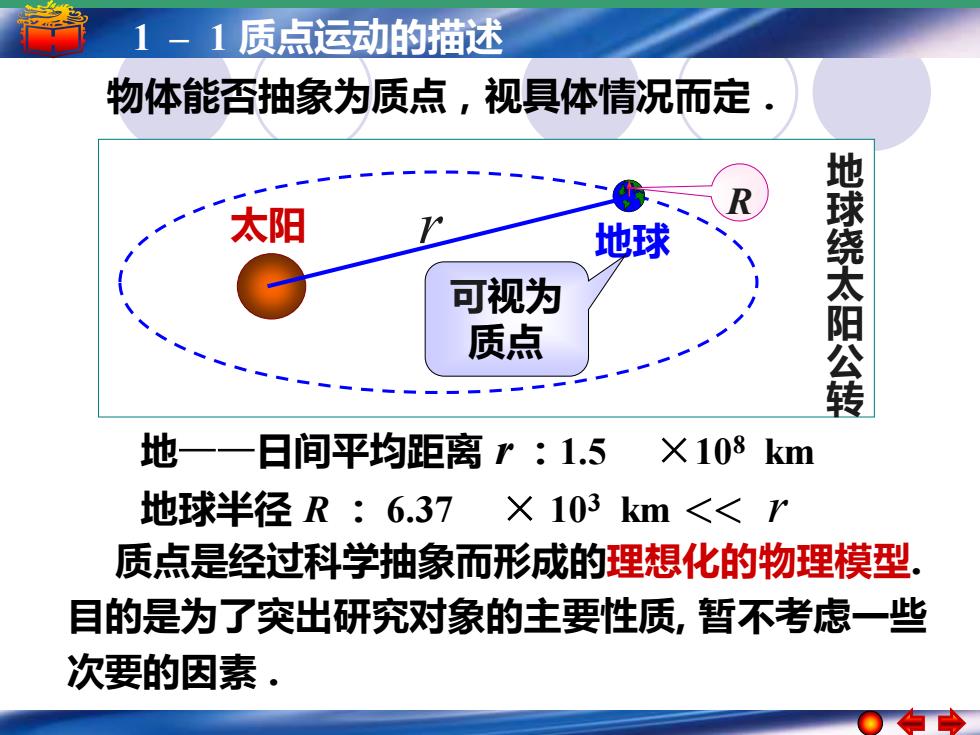
1-1质点运动的描述 物体能否抽象为质点,视具体情况而定 太阳 地球 可视为 质点 地球绕太阳公转 地一一日间平均距离r:1.5 ×108km 地球半径R:6.37×103km<<r 质点是经过科学抽象而形成的理想化的物理模型, 目的是为了突出研究对象的主要性质,暂不考虑一些 次要的因素
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 物体能否抽象为质点,视具体情况而定. 质点是经过科学抽象而形成的理想化的物理模型. 目的是为了突出研究对象的主要性质, 暂不考虑一些 次要的因素 . 太阳 r 地球 R 地 球 绕 太 阳 公 转 地——日间平均距离 r :1.5 ×108 km 地球半径 R : 6.37 × 103 km r 可视为 质点
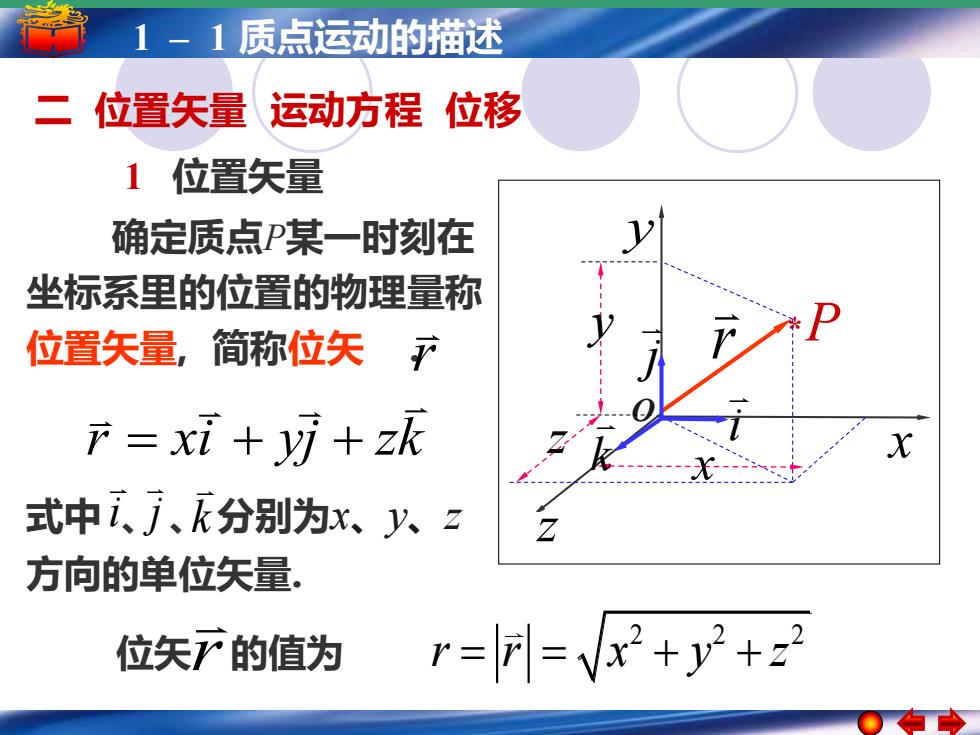
1-1质点运动的描述 二 位置矢量运动方程位移 1位置矢量 确定质点P某一时刻在 坐标系里的位置的物理量称 位置矢量,简称位矢产 产=xi+yi+z 式中ij、分别为x、八2 方向的单位矢量, 位矢?的值为 r=F=vx+y+2
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 x z y O 二 位置矢量 运动方程 位移 1 位置矢量 r * P x y r xi yj zk z = + + 2 2 2 位矢 r 的值为 r r x y z = = + + 确定质点P某一时刻在 坐标系里的位置的物理量称 位置矢量, 简称位矢 . r 式中 、 、 分别为x、y、z 方向的单位矢量. i j k i k j
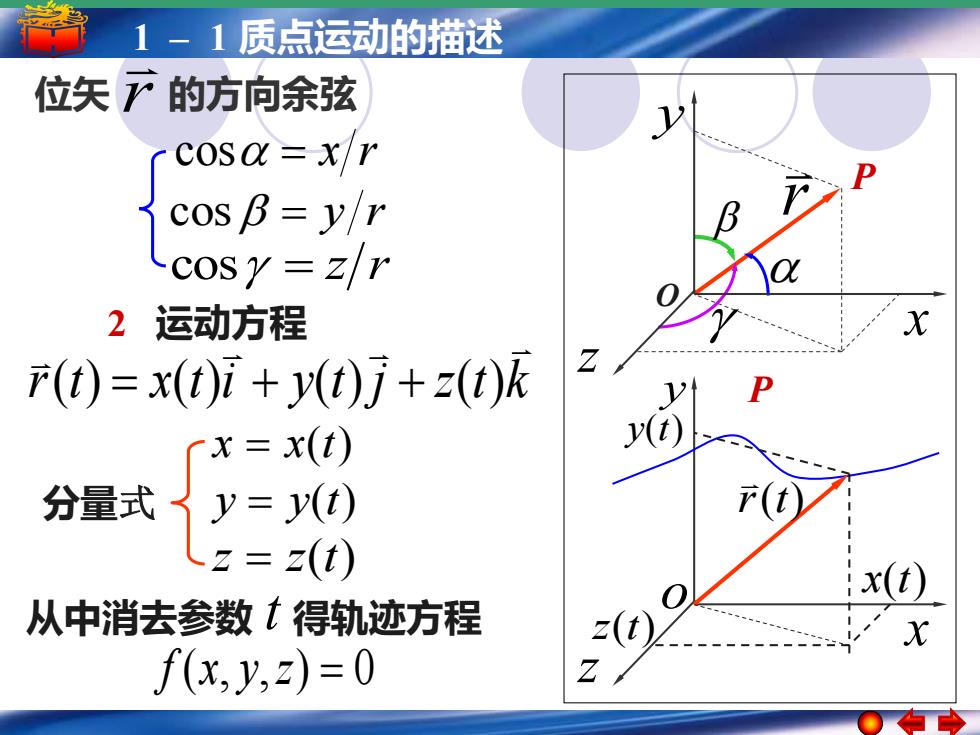
1-1质点运动的描述 位矢下的方向余弦 cosa=x/r cos B=y/r -cosy=z/r 2运动方程 F(t)=x(t)i+y(t)j+z(t)k Z cx=x(t) y(t) 分量式了y=y(t) 、2=z(t) (t) 从中消去参数t得轨迹方程 (t) f(x,y,z)=0
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 cos = x r cos = z r cos = y r 位矢 r 的方向余弦 P P r x z y o 2 运动方程 r t x t i y t j z t k ( ) = ( ) + ( ) + ( ) x = x(t) y = y(t) z = z(t) 分量式 从中消去参数 得轨迹方程 f (x, y,z) = 0 t r(t) x(t) y(t) z(t) x z y O
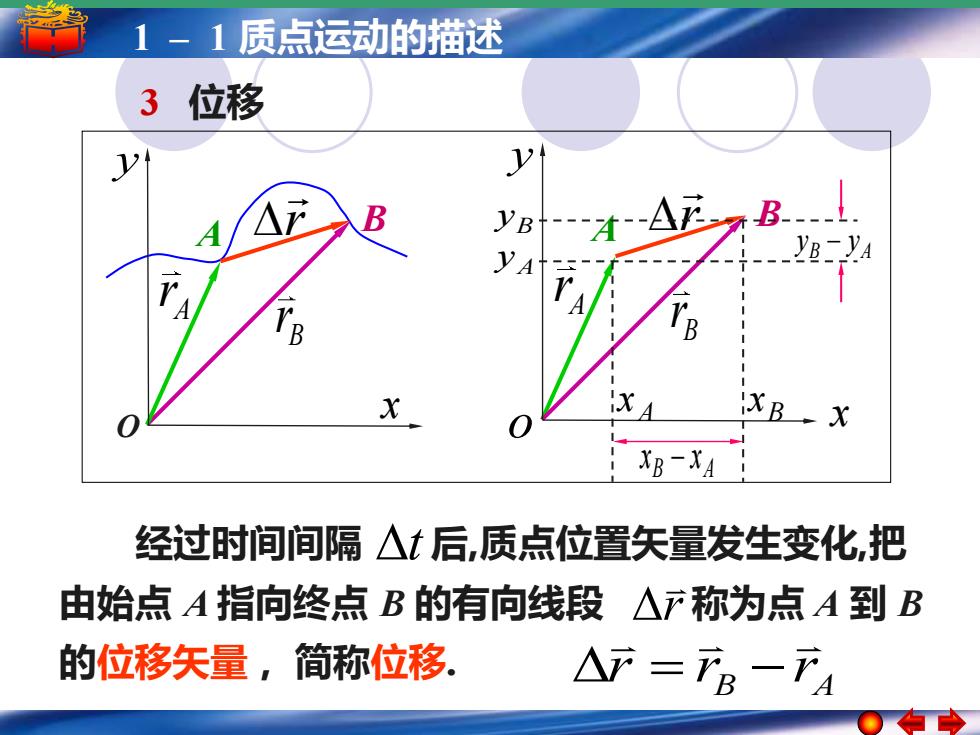
1-1质点运动的描述 3 位移 B yB-A7B. YB-YA B XBX :XR-XA 经过时间间隔△后,质点位置矢量发生变化把 由始点A指向终点B的有向线段△F称为点A到B 的位移矢量,简称位移。 △F=产B一FA
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 3 位移 B B r A r A r A r B B r A r x y o B x A x B A x − x B y A y B A y − y 经过时间间隔 后,质点位置矢量发生变化,把 由始点 A 指向终点 B 的有向线段 称为点 A 到 B 的位移矢量 , 简称位移. B A r r r = − t r x y O
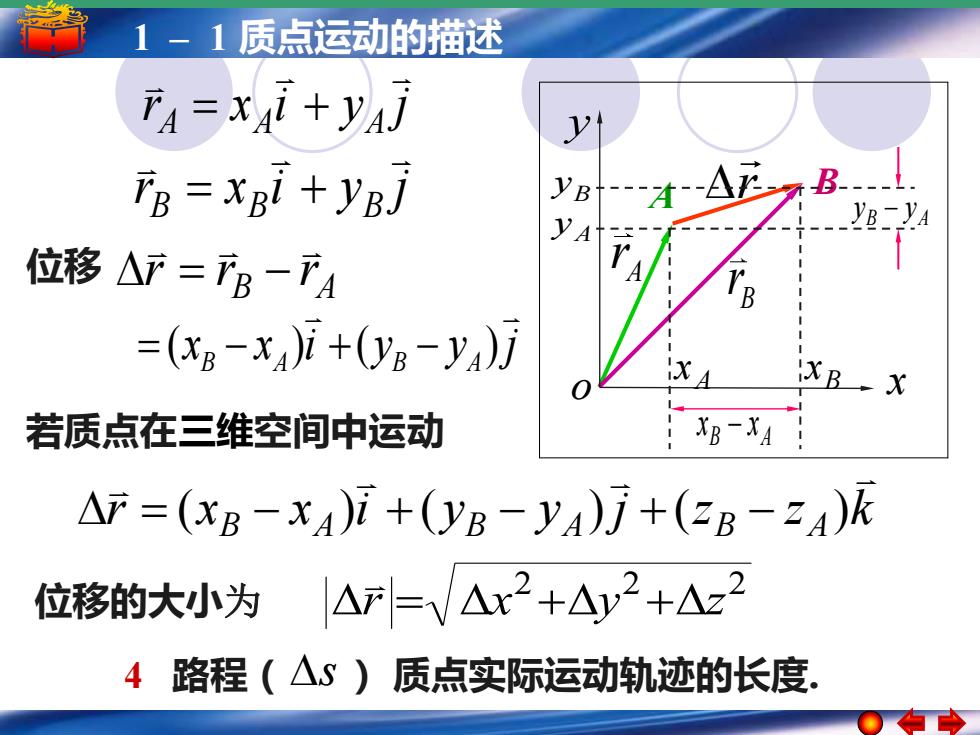
1-1质点运动的描述 TA=xAi+yaj 2 Tg=xgi+ygj yB B- yA _YB-YA 位移△产=B一下4 =(xg-x4)i+(0yB-yA)万 XBX 若质点在三维空间中运动 XB-XA △F=(xB-xA)i+(yB-yA)万j+(3B-2A)k 位移的大小为 △F=V△2+△y2+△z2 4路程(△S)质点实际运动轨迹的长度
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 2 2 2 r = x +y +z 位移的大小为 A r B B r A r x y o B x A x B A x − x B y A y B A y − y r x i y j A A A = + r x i y j B B B = + x x i y y j B A B A = ( − ) +( − ) B A r r r 位移 = − 若质点在三维空间中运动 r x x i y y j z z k B A B A B A = ( − ) + ( − ) + ( − ) 4 路程(s ) 质点实际运动轨迹的长度
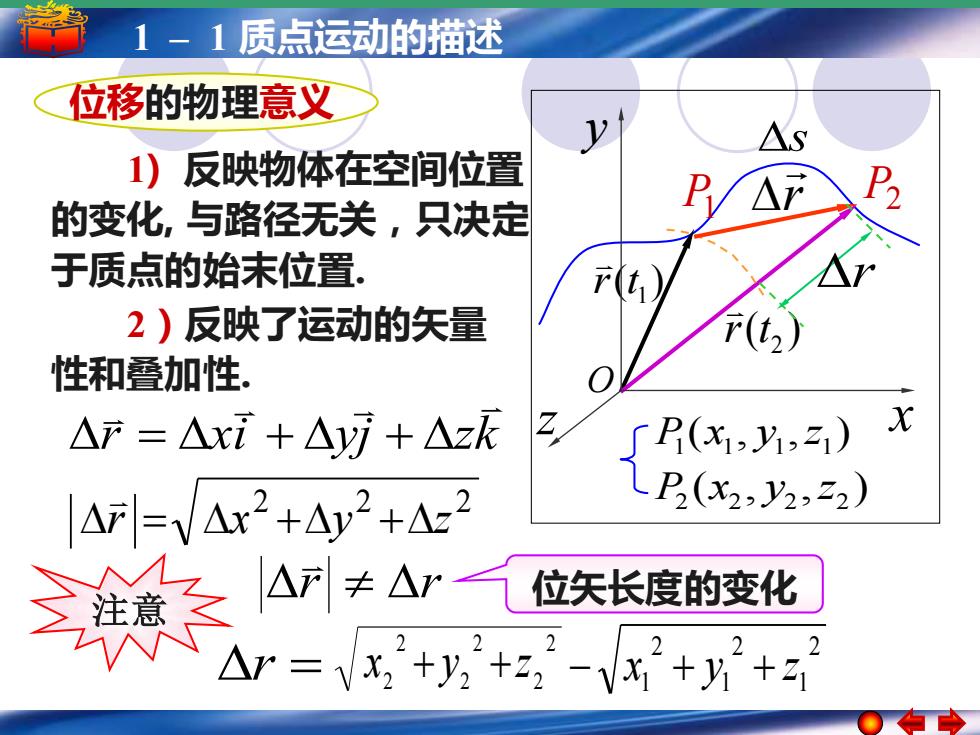
1-1质点运动的描述 位移的物理意义 1 A.S 1)反映物体在空间位置 的变化,与路径无关,只决定 于质点的始末位置, 2)反映了运动的矢量 性和叠加性。 △产=△xi+△yi+△zk ∫P(x,2) △F=V△2+△y2+△c2 LP2(x2,y2,22) 三注意 A产≠△r 位矢长度的变化 △=yx+y,+-x2+y+
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 2 2 2 r = x +y +z r r 2 1 2 1 2 1 − x + y + z 2 2 2 2 2 2 r = x + y +z 位移的物理意义 1) 反映物体在空间位置 的变化, 与路径无关,只决定 于质点的始末位置. 2)反映了运动的矢量 性和叠加性. s ( , , ) 1 1 1 1 P x y z ( , , ) 2 2 2 2 P x y z ( ) 1 r t P1 ( ) 2 r t r P2 注意 x y O z r r xi yj zk = + + 位矢长度的变化

1-1质点运动的描述 讨论 位移与路程 (1)P1、P2两点间的路程 是不唯一的,可以是△或 △S 而位移人是唯一的, (2)一般情况,位移 大小不等于路程 △r≠△y (3)只有在不改变方向的直线运动中. △F=△S (4)位移是矢量,路程是标量
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 位移与路程 (2) 一般情况, 位移 大小不等于路程. r s (4)位移是矢量, 路程是标量. s ( ) 1 r t P1 ( ) 2 r t r P2 x y O z s (3)只有在不改变方向的直线运动中. r = s 讨论 (1)P1、P2 两点间的路程 是不唯一的, 可以是 或 而位移 r 是唯一的. s s
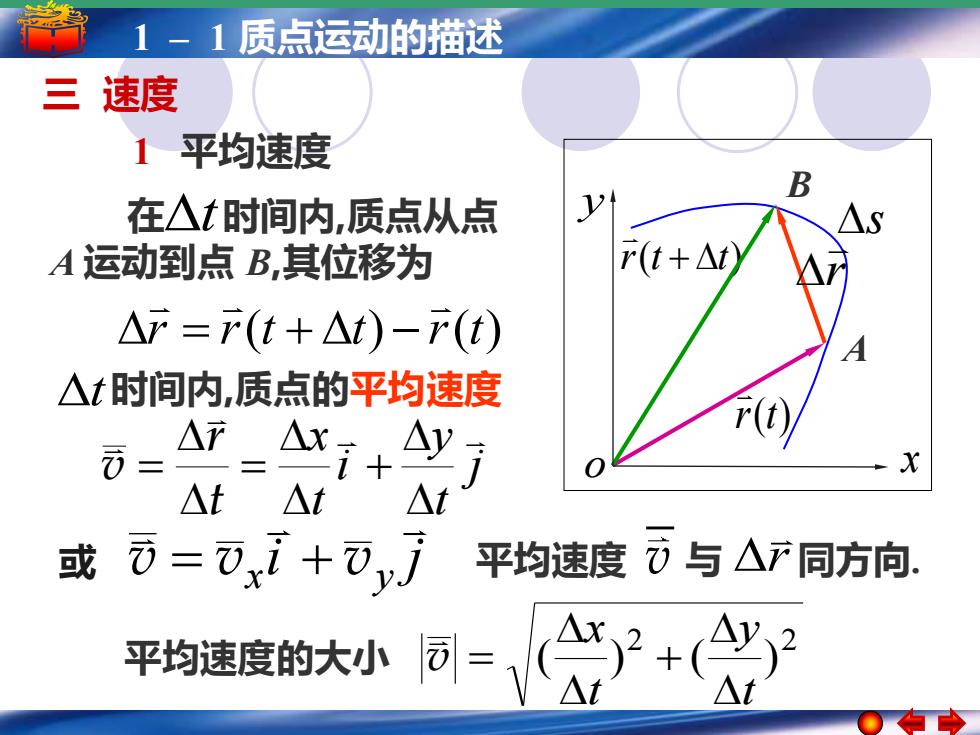
1-1质点运动的描述 三速度 1平均速度 B 在△t时间内,质点从点 A运动到点B,其位移为 r(t+△t △产=F(t+△t)-产(t) △t时间内,质点的平均速度 F_△xi+Ay方 4 △t △t △t 元=0xi+⑦yj 或 平均速度与△产同方向 平均速度的大小可=(心2+(
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 三 速度 1 平均速度 r r(t t) r(t) = + − 在 时间内,质点从点 A 运动到点 B,其位移为 t t 时间内,质点的平均速度 平均速度 与 r 同方向. v j t y i t x + = = t r v 平均速度的大小 2 2 ( ) ( ) t y t x + v = i j x y 或 v = v + v r r(t + t) B r(t) A x y o s

1-1质点运动的描述 2瞬时速度 当△→0时平均速度的极限值叫做瞬时速度, 简称速度 △F dr δ= lim △t→0△t dt △x () ⑦=lim +lim △t-→0△t △t-→0△t 当△t→0时,dr=ds F(t+△) ds dt x 当质点做曲线运动时,质点在某一点的速度方向 就是沿该点曲线的切线方向
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 2 瞬时速度 当质点做曲线运动时,质点在某一点的速度方向 就是沿该点曲线的切线方向 . 当 时平均速度的极限值叫做瞬时速度, 简称速度 t →0 j t y i t x t t + = →0 →0 v lim lim t r t r t d d lim 0 = = → v dr = ds 当 t → 0 时, t d d e t s v =