
第三章 刚体和流体
第三章 刚体和流体

§3-1刚体及其运动规律 刚体:物体上任意两点之间的距离保持不变 在力的作用下不发生形变的物体
§3-1 刚体及其运动规律 刚体:物体上任意两点之间的距离保持不变 在力的作用下不发生形变的物体
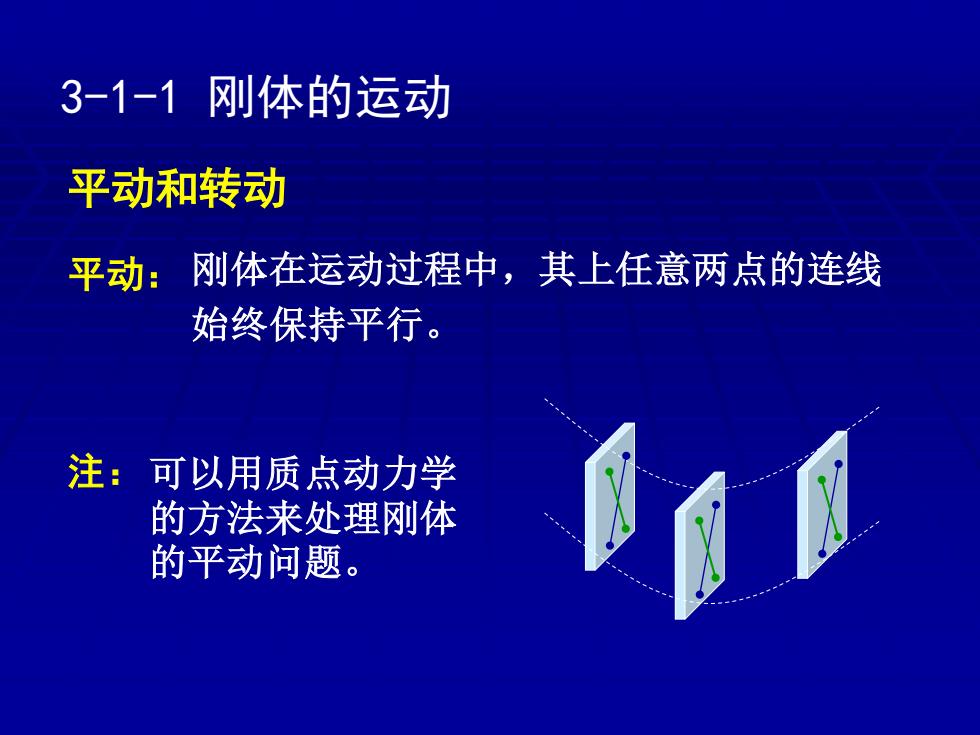
3-1-1刚体的运动 平动和转动 平动 :刚体在运动过程中,其上任意两点的连线 始终保持平行。 注:可以用质点动力学 的方法来处理刚体 的平动问题
3-1-1 刚体的运动 平动和转动 平动: 刚体在运动过程中,其上任意两点的连线 始终保持平行。 可以用质点动力学 的方法来处理刚体 的平动问题。 注:

转动:刚体上所有质点都绕同一直线做圆周运 动。这种运动称为刚体的转动。这条直 线称为转轴。 定轴转动: 转轴固定不动的转动。 112 3
转动:刚体上所有质点都绕同一直线做圆周运 动。这种运动称为刚体的转动。这条直 线称为转轴。 定轴转动: 转轴固定不动的转动

3-1-2 刚体对定轴的角动量 质元:组成物体的微颗粒元 质元对点的角动量为 L,=R×(m,o,) L,=mR0 L,沿转轴Oz的投影为 L=L,cos(2)=m,R0,sm7
3-1-2 刚体对定轴的角动量 质元:组成物体的微颗粒元 质元对点的角动量为 ( ) Li Ri mi i v = Li = mi Ri vi Li 沿转轴Oz的投影为 ) 2 π = cos( − Li z Li sin = mi Ri vi z Li O x y mi i r Ri vi

L.=m,0,=m,r0 刚体对Oz轴的角动量为 L.=∑L.-∑mrio=(mro 令 .=Σy 单位:kgm2 J为刚体对Oz轴的转动惯量。 L2=J20
i i i = m r v 2 i i = m r Liz 刚体对Oz轴的角动量为 = = = i i i i i i i z i z L L m r ( m r ) 2 2 令 = i z i i J m r 2 J z 为刚体对 Oz 轴的转动惯量。 Lz = J z 2 单位: kgm

结论:刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体: J=fr'dm=f,plr J=fdm=[y"ars (面质量分布) J=Jy"dm=Sr"ndi (线质量分布)
刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 结论: 对于质量连续分布的刚体: = = V V J r dm r dV 2 2 = = S S J r dm r dS 2 2 (面质量分布) = = L L J r dm r dl 2 2 (线质量分布)

例1计算质量为m,长为l的细棒绕一端的转动惯量。 解:J=∫r2dm dn=pds=%d dm r2=x2 -s-m
例1 计算质量为m,长为l 的细棒绕一端的转动惯量。 o x z J r dm 2 解: = x l m dm = dx = d 2 2 r = x l l x l m x l m J x 0 3 0 2 3 1 = d = 2 3 1 J = ml dx dm x O

例2一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。 解: dm=o2元rdr J=∫r2dm=2mo∫rd J=2πordn πoR=1 2-2
o R 例2 一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。 解: dm = 2π rdr J = r dm 2 = 2π r dr 3 = R J r r 0 3 2π d 2 4 2 1 2 π mR R = = r dr
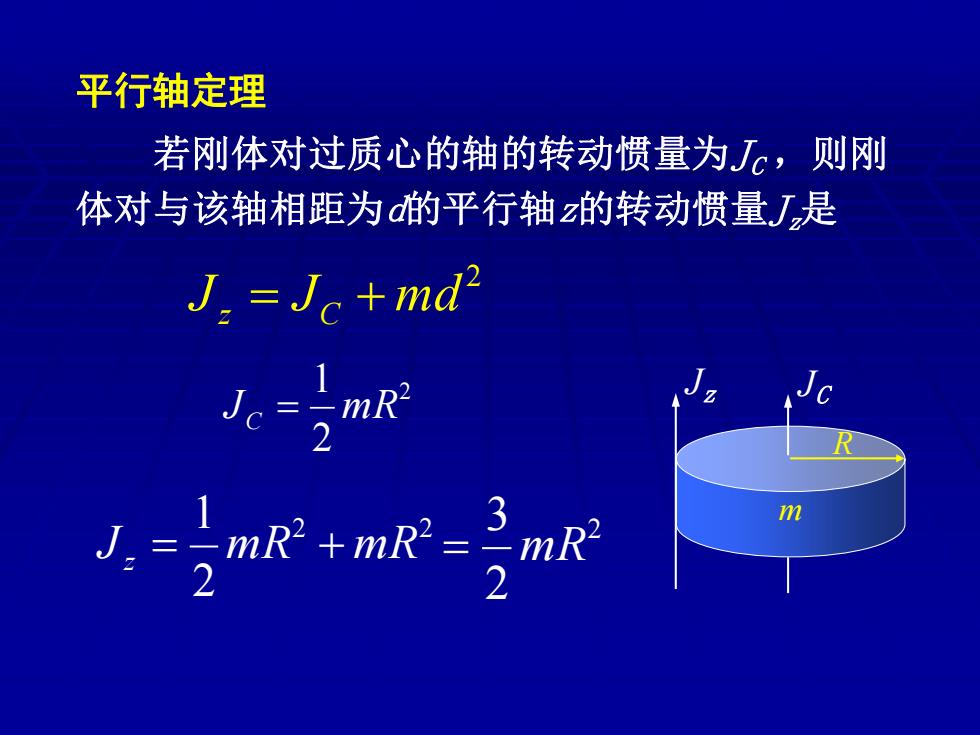
平行轴定理 若刚体对过质心的轴的转动惯量为J,则刚 体对与该轴相距为d的平行轴z的转动惯量J是 J.=Jc+md2 .-mR'+m-3mk
m R Jz 平行轴定理 若刚体对过质心的轴的转动惯量为JC ,则刚 体对与该轴相距为d的平行轴z的转动惯量Jz是 2 J J md z = C + 2 JC 2 1 JC = mR 2 2 2 1 Jz = mR + mR 2 2 3 = mR