
混沌简介 1.什么是混沌 混沌是决定论系统所表现的随机行为的总称。它的根源在于非线性的相互作用。 所谓“决定论系统“是指描述该系统的数学模型是不包含任何随机因素的完全确定的方 自然界中最常见的运动形态往往既不是完全确定的,也不是完全随机的,关于混池现象 的理论,为我们更好地理解自然界提供了一个框架。 混沌的数学定义有很多种。例如,正的“拓扑熵“定义拓扑混沌:有限长的“转动区间“定 义转动混沌等等。这些定义都有严格的数学理论和实际的计算方法。不过,要把某个数学模 型或实验现象明白无误地纳入某种混沌定义并不容易。因此,一般可使用下面的混沌工作定 义。 若所处理的动力学过程是确定的,不包含任何外加的随机因素:单个轨道表现出像是随 机的对初值细微变化极为敏感的行为,同时一些整体性的经长时间平均或对大量轨道平均所 得到的特征量又对初值变化并不敏感:加之上述状态又是经过动力学行为和一系列突变而达 到的。那么,你所研究的现象极有可能是混沌。 2.非线性 “线性”与“非线性”我们是熟悉的,常用于区别函数y=x)对自变量x的依赖关系。 线性函数即一次函数,其图像为一条直线。其它函数则为非线性函数,其图像不是直线。非 线性关系虽然千变万化,但还是具有某些不同于线性关系的共性。 线性关系是互不相干的独立贡献,而非线性则是相互作用,而正是这种相互作用,使得 整体不再是简单地等于部分之和,而可能出现不同于“线性叠加“的增益或亏损。 线性关系保持讯号的频率成分不变,而非线性则使频率结构发生变化。只要存在非线性 哪怕是任意小的非线性,就会出现和频、差频、倍频等成分,这是我们所熟悉的
1.什么是混沌 混沌是决定论系统所表现的随机行为的总称。它的根源在于非线性的相互作用。 所谓"决定论系统"是指描述该系统的数学模型是不包含任何随机因素的完全确定的方 程。 自然界中最常见的运动形态往往既不是完全确定的,也不是完全随机的,关于混沌现象 的理论,为我们更好地理解自然界提供了一个框架。 混沌的数学定义有很多种。例如,正的"拓扑熵"定义拓扑混沌;有限长的"转动区间"定 义转动混沌等等。这些定义都有严格的数学理论和实际的计算方法。不过,要把某个数学模 型或实验现象明白无误地纳入某种混沌定义并不容易。因此,一般可使用下面的混沌工作定 义。 若所处理的动力学过程是确定的,不包含任何外加的随机因素;单个轨道表现出像是随 机的对初值细微变化极为敏感的行为,同时一些整体性的经长时间平均或对大量轨道平均所 得到的特征量又对初值变化并不敏感;加之上述状态又是经过动力学行为和一系列突变而达 到的。那么,你所研究的现象极有可能是混沌。 2.非线性 “线性”与“非线性”我们是熟悉的,常用于区别函数 y = f (x)对自变量 x 的依赖关系。 线性函数即一次函数,其图像为一条直线。其它函数则为非线性函数,其图像不是直线。非 线性关系虽然千变万化,但还是具有某些不同于线性关系的共性。 线性关系是互不相干的独立贡献,而非线性则是相互作用,而正是这种相互作用,使得 整体不再是简单地等于部分之和,而可能出现不同于"线性叠加"的增益或亏损。 线性关系保持讯号的频率成分不变,而非线性则使频率结构发生变化。只要存在非线性, 哪怕是任意小的非线性,就会出现和频、差频、倍频等成分,这是我们所熟悉的

非线性是引起行为突变的原因,对线性的微小偏离,一般并不引起行为突变,而且可以 从原来的线性情况出发,用修正的线性理论去描述和理解。但当非线性大到一定程度时,系 统行为就可能发生突变。非线性系统往往在一系列参量阀值(参量阀值指系统参量达到此临 界值时才出现突变行为)上发生突变,每次突变都伴随着某种新的频率成分,系统最终进入 混沌状态。 从非线性的上述特点可以看到,若系统出现混池现象,则系统必定是一个非线性系统。 非线性系统进入混沌状态是一种突变行为。 如何判断系统是否进入混沌状态,即如何区分是否是长周期现象,如何区分系统是否受 到外来的随机干扰等等,是研究混沌现象的重要问题。 3.通向混沌之路 一个简单的一维虫口模型(也称逻辑斯蒂映射),能够表现出许多典型的混沌行为。这 是一个生态模型,抽象的标准虫口方程是 xH=1-x】 其中,X的变化范围是[0,1,而参量“通常在0到4之间取值。 这是一个选代方程,可用作图方式形象表示迭代过程:图中画出根据给定的“对应的非 线性函数了)=公1-为和直线y=,取初值。,在是符到相应的产,过该点作水 平线与y=x的交点的横坐标即,如此继续,可完成迭代过程。 计算发现,当4=25时,对任意的,经过有限步骤,都得到x=Q6,即x=06是 个不动点,也就是说,最终状态对初值的变化不敏感,或说,不动点是一个吸引子
非线性是引起行为突变的原因,对线性的微小偏离,一般并不引起行为突变,而且可以 从原来的线性情况出发,用修正的线性理论去描述和理解。但当非线性大到一定程度时,系 统行为就可能发生突变。非线性系统往往在一系列参量阈值(参量阈值指系统参量达到此临 界值时才出现突变行为)上发生突变,每次突变都伴随着某种新的频率成分,系统最终进入 混沌状态。 从非线性的上述特点可以看到,若系统出现混沌现象,则系统必定是一个非线性系统。 非线性系统进入混沌状态是一种突变行为。 如何判断系统是否进入混沌状态,即如何区分是否是长周期现象,如何区分系统是否受 到外来的随机干扰等等,是研究混沌现象的重要问题。 3.通向混沌之路 一个简单的一维虫口模型(也称逻辑斯蒂映射),能够表现出许多典型的混沌行为。这 是一个生态模型,抽象的标准虫口方程是 其中, 的变化范围是[0,1],而参量 通常在 0 到 4 之间取值。 这是一个迭代方程,可用作图方式形象表示迭代过程:图中画出根据给定的 对应的非 线性函数 和直线 y = x,取初值 ,在 f(x)是得到相应的 ,过该点作水 平线与 y = x 的交点的横坐标即 ,如此继续,可完成迭代过程。 计算发现,当 时,对任意的 ,经过有限步骤,都得到 x = 0.6,即 x = 0.6 是一 个不动点,也就是说,最终状态对初值的变化不敏感,或说,不动点是一个吸引子
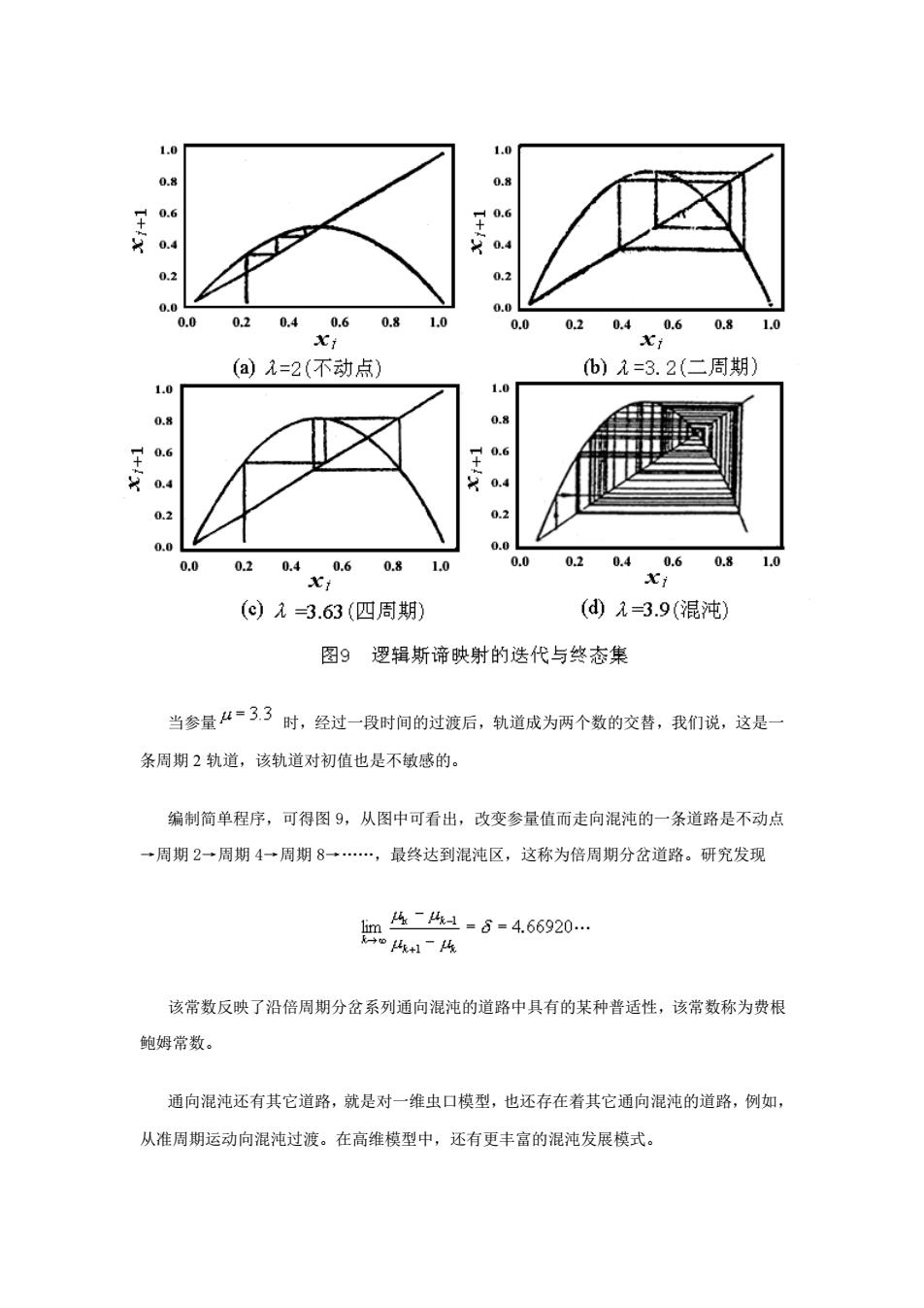
1.0 1.0 0.2 0.2 0.0 0.0 0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.40.6 0.8 1.0 Xi Xi (a九=2(不动点) b)元=3.2(二周期) 1.0 0 0.8 6 0.6 0.4 0.4 0.2 0.2 0.0 0.0 0.0 0.2 0.40.6 0.8 L.0 0.0 0.2 0.40.6 0.8 1.0 Xi (c)元=3.63(四周期) (④元=3.9(混沌) 图9逻辑斯谛映射的迭代与终态集 当参量4=33时,经过一段时间的过渡后,轨道成为两个数的交替,我们说,这是一 条周期2轨道,该轨道对初值也是不敏感的。 编制简单程序,可得图9,从图中可看出,改变参量值而走向混沌的一条道路是不动点 一周期2→周期4→周期8→.,最终达到混沌区,这称为倍周期分岔道路。研究发现 4-4%1=6=4.66920. 职一4 该常数反映了沿倍周期分岔系列通向混沌的道路中具有的某种普适性,该常数称为费根 鲍姆常数。 通向混沌还有其它道路,就是对一维虫口模型,也还存在着其它通向混沌的道路,例如, 从准周期运动向混沌过渡。在高维模型中,还有更丰富的混沌发展模式
当参量 时,经过一段时间的过渡后,轨道成为两个数的交替,我们说,这是一 条周期 2 轨道,该轨道对初值也是不敏感的。 编制简单程序,可得图 9,从图中可看出,改变参量值而走向混沌的一条道路是不动点 →周期 2→周期 4→周期 8→.,最终达到混沌区,这称为倍周期分岔道路。研究发现 该常数反映了沿倍周期分岔系列通向混沌的道路中具有的某种普适性,该常数称为费根 鲍姆常数。 通向混沌还有其它道路,就是对一维虫口模型,也还存在着其它通向混沌的道路,例如, 从准周期运动向混沌过渡。在高维模型中,还有更丰富的混沌发展模式