
电港汤与电雅酒 第5章均匀平面波在无界媒质中的传播 新章均均平面泼无界空间中的转督 I
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 1
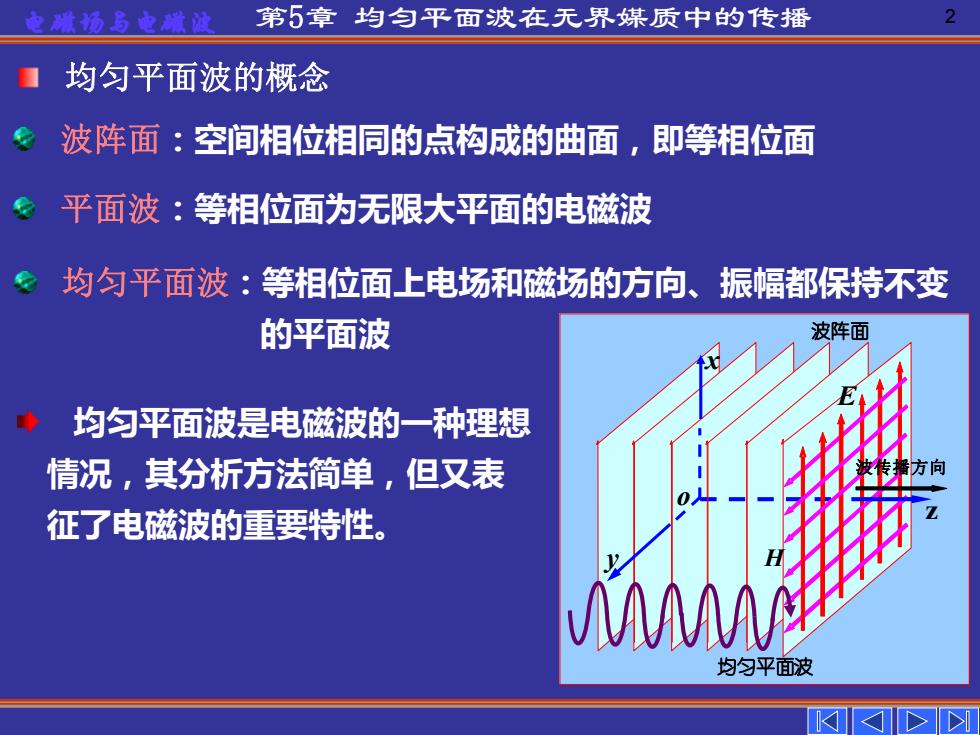
第5章均匀平面波在无界媒质中的传播 2 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 。均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变 的平面波 波阵面 ◆ 均匀平面波是电磁波的一种理想 情况,其分析方法简单,但又表 征了电磁波的重要特性。 M 均匀平面波
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 2 E H z 波传播方向 均匀平面波 波阵面 x y o 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变 的平面波 均匀平面波是电磁波的一种理想 情况,其分析方法简单,但又表 征了电磁波的重要特性

电港汤与电雅酒 第5章均匀平面波在无界媒质中的传播 3 本章内容 5.1 理想介质中的均匀平面波 5.2电磁波的极化 5.3导电媒质中的均匀平面波 5.4色散与群速 5.5均匀平面波在各向异性媒质中的传播 KKDH
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 3 本章内容 5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速 5.5 均匀平面波在各向异性媒质中的传播

电雅汤与电雅波 第5章均匀平面波在无界媒质中的传播 4 5.1理想介质中的均匀平面波 5.1.1一维波动方程的均匀平面波解 5.1.2理想介质中均匀平面波的传播特点 5.1.3沿任意方向传播的均匀平面波
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 4 5.1 理想介质中的均匀平面波 5.1.1 一维波动方程的均匀平面波解 5.1.2 理想介质中均匀平面波的传播特点 5.1.3 沿任意方向传播的均匀平面波

电雅汤与电雅道 第5章均匀平面波在无界媒质中的传播 5 5.1.1一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想 介质。均匀平面波沿z轴传播,则电场强度和磁场强度均不是x 和y的函数,即 证_正=0, aH OH d Ox ay -0→ d+=0. 正+k7=0 由于V.E=兆E 20 → OE. 20 E=0 8x 8 同理7,户= OH,OH,OH o"e 三=0◆ H.=0 +k2E=0 8x d22 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播 方向一横电磁波(TEM波)
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 5 0 x y z E E E E x y z = + + = 由于 5.1.1 一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想 介质。均匀平面波沿 z 轴传播,则电场强度和磁场强度均不是 x 和 y 的函数,即 0 , 0 E E H H x y x y = = = = 0 E z z = 0 E z = 2 2 2 2 2 2 d d 0 , 0 d d E H k E k H z z + = + = 2 2 2 0 z z E k E z + = 同理 0 x y z H H H H x y z = + + = 0 H z = 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播 方向 —— 横电磁波(TEM波)
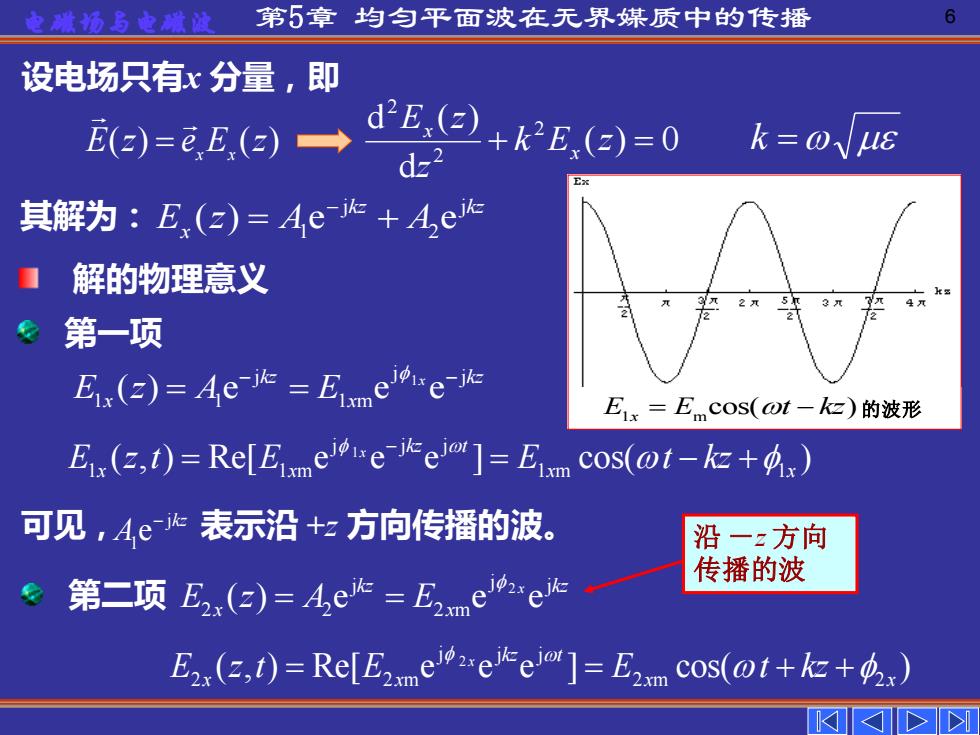
电雅汤马电雅波 第5章均匀平面波在无界媒质中的传播 6 设电场只有x分量,即 E(z)=eE(2)→ dE(@)+kE,(a)=0 k=0JuE dz2 其解为:E.(z)=Aejk+A,e 解的物理意义 第一项 Eix()=heik Eimee 1x=Emcos(ot-kz)的波形 E(=,t)=Re[Ee]=Eim Cos(t-k+) 可见,Ae北表示沿+z方向传播的波。 沿一z方向 传播的波 第二项E2,(a)=A,e=E E(t)=Re[Ei]=E2m Cos(t+) >
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 6 1 j j j 1 1 1 m ( ) e e e kz kz x E z A E x x − − = = 1 j j j 1 1 m 1 m 1 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x − = = − + ( ) 0 d d ( ) 2 2 2 + k E z = z E z x x E(z) e E (z) k = x x = 设电场只有x 分量,即 j j 1 2 ( ) e e kz kz E z A A x − 其解为: = + 可见, A1 e − jkz 表示沿 +z 方向传播的波。 E E t kz 1 m x = − cos( ) 的波形 解的物理意义 第一项 2 j j j 2 2 2 m ( ) e e e kz kz x E z A E x x = = 2 j j j 2 2 m 2 m 2 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x = = + + 第二项 沿 -z 方向 传播的波

电汤与电雅 第5章均匀平面波在无界媒质中的传播 相伴的磁场 磁场与电场相互 由V×E=-jouH,可得 垂直,且同相位 ×eEx=-e ou 6z 其中ni, B:=称媒质的本征阻抗。在真空中 7=7% =120π≈3772 同理,对于E2=eE2x=eA,ek→i2=(-e)xE, 结论:在理想介质中,均匀平面波的电场强度与磁场强度相 互垂直,且同相位
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 7 1 1 1 1 1 j 1 x y y x z x x z E k H e e E e e E e E z = = = = 由 = − E H j ,可得 ( ) 1 1 = = y x H E 其中 称为媒质的本征阻抗。在真空中 = = =120 377 0 0 0 相伴的磁场 同理,对于 j 2 2 2e kz E e E e A = = x x x 2 2 ( ) 1 H ez E = − 磁场与电场相互 垂直,且同相位 结论:在理想介质中,均匀平面波的电场强度与磁场强度相 互垂直,且同相位
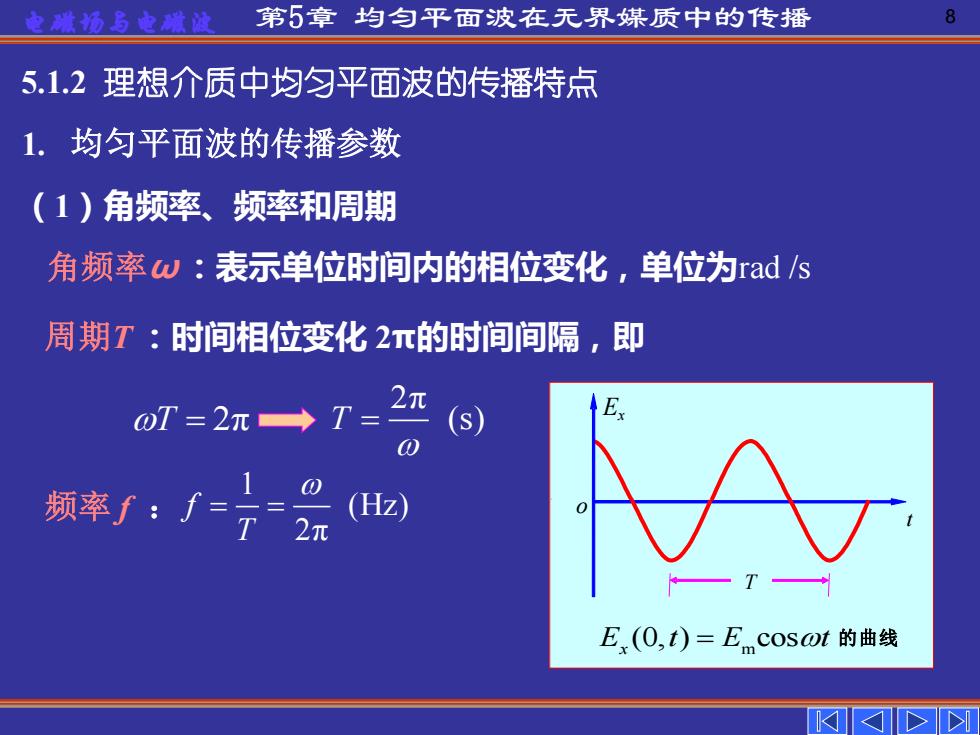
第5章均匀平面波在无界媒质中的传播 8 5.1.2理想介质中均匀平面波的传播特点 1.均匀平面波的传播参数 (1)角频率、频率和周期 角频率w:表示单位时间内的相位变化,单位为rads 周期T:时间相位变化2π的时间间隔,即 wM=2π→7=2元 (s) 频率f:f=元=。 (Hz) -T2π E,(0,t)=E cosot的曲线
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 8 1. 均匀平面波的传播参数 周期T :时间相位变化 2π的时间间隔,即 (1)角频率、频率和周期 角频率ω:表示单位时间内的相位变化,单位为rad /s 频率 f : 1 (Hz) 2π f T = = t T o Ex E t E t x (0, ) cos = m 的曲线 2π T (s) T = 2π = 5.1.2 理想介质中均匀平面波的传播特点
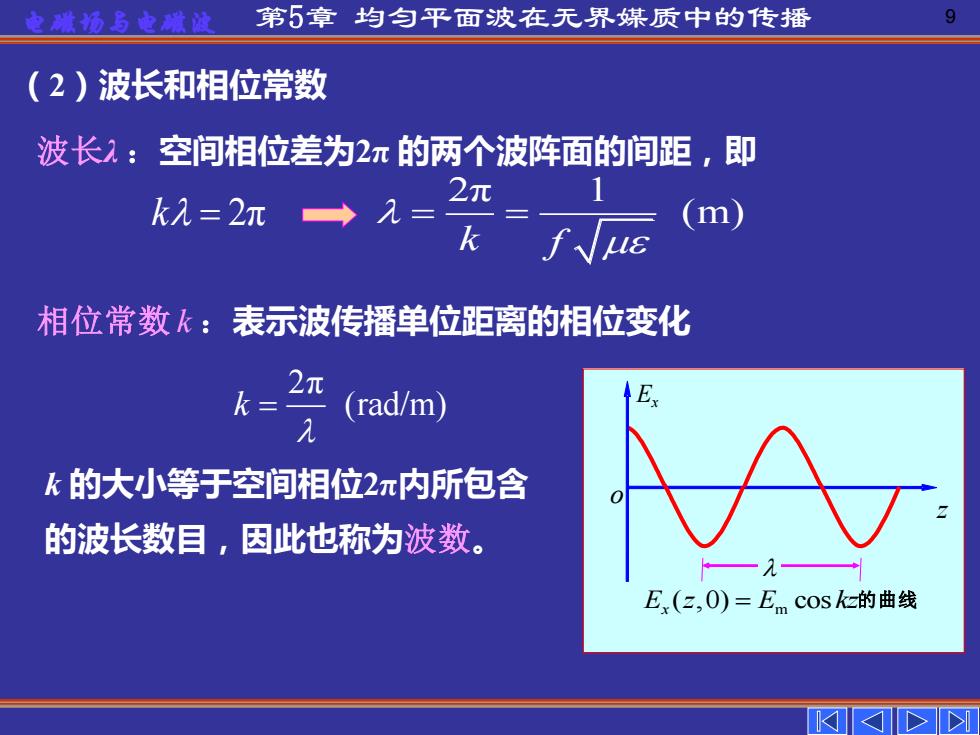
电雅汤与电雕道 第5章均匀平面波在无界媒质中的传播 9 (2)波长和相位常数 波长):空间相位差为2π的两个波阵面的间距,即 k2=2m2= 2元 (m) 相位常数飞:表示波传播单位距离的相位变化 k=2红 (rad/m) k的大小等于空间相位2π内所包含 的波长数目,因此也称为波数。 E(2,0)=E cos kz的曲线
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 9 (2)波长和相位常数 k 的大小等于空间相位2π内所包含 的波长数目,因此也称为波数。 2π k (rad/m) = 波长λ :空间相位差为2π 的两个波阵面的间距,即 相位常数 k :表示波传播单位距离的相位变化 o Ex z E z E kz x ( ,0) cos = m 的曲线 2π 1 (m) k f k = 2π = =
电雅汤马电雅波 第5章均匀平面波在无界媒质中的传播 10 (3)相速(波速) 相速y:电磁波的等相位面在空间 中的移动速度 由ot-kz=C→odt-kdb=0 故得到均匀平面波的相速为 dz w 相速只与媒质参数 (m/s) 有关,而与电磁波 dt k 的频率无关 真空中:v=c= =3×108(m/s) 4rx10-7 1×109 36
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播 10 (3)相速(波速) (m s) 1 d d = = = = t k z v 真空中: 8 0 0 7 9 1 1 3 10 (m/s) 1 4π 10 10 36π v c − − = = = = 由 t −kz =C 相速v:电磁波的等相位面在空间 中的移动速度 相速只与媒质参数 有关,而与电磁波 的频率无关 故得到均匀平面波的相速为 d d 0 t k z − =