《电磁场理论》课程电子教案（讲义）第三章 静态场及其边值问题的解

第3章静态电磁场及其边值问题的解 第4章0 静态电磁场：场量不随时间变化，包括：静电场、恒定电场和恒定磁场 时变情况下，电场和磁场相互关联，构成统一的电磁场 静态情况下，电场和磁场由各自的源激发，且相互独立 本章内容 3.1静电场分析 3.2导电媒质中的恒定电场分析 3.3恒定磁场分析 3.4静态场的边值问题及解的惟一性定理 3.5镜像法 36分离变量 3.1静电场分析 静电场的应用： 静电放电：高电压测量测量中用到的球隙 静电感应：传感器，电容式物位计。 静电屏蔽：高电压实验室，微波暗室，通信电缆等 电场力的应用：电子管，晶体管，阴极射线管，显像管，静电发电机，静电电动机，回旋加速器。 工业：静电除尘，静电分离，静电喷漆，静电复印机。 静电场的危害：静电感应引起高压电线对周围的影响。静电引发火灾，静电防护。 3.1静电场分析 本节内容 311 静电场的基本方程和边界条件 3.1.2 电位函数 313 导体系统的电容与部分电容 3.1.4 静电场的能量 3.1.5静电力 3.1.1静电场的基本方程和边界条件 1.基本方程 (V.D=p f.D.ds=g 微分形式 fE-di=0 积分形式 7×E=0 D=E本构关系 2.边界条件

1 第3章 静态电磁场及其边值问题的解 第4章 () 静态电磁场：场量不随时间变化，包括：静电场、恒定电场和恒定磁场 时变情况下，电场和磁场相互关联，构成统一的电磁场 静态情况下，电场和磁场由各自的源激发，且相互独立 本章内容 3.1 静电场分析 3.2 导电媒质中的恒定电场分析 3.3 恒定磁场分析 3.4 静态场的边值问题及解的惟一性定理 3.5 镜像法 3.6 分离变量法 3.1 静电场分析 静电场的应用： 静电放电：高电压测量测量中用到的球隙 静电感应：传感器，电容式物位计。 静电屏蔽：高电压实验室，微波暗室，通信电缆等 电场力的应用：电子管，晶体管，阴极射线管，显像管，静电发电机，静电电动机，回旋加速器。 工业：静电除尘，静电分离，静电喷漆，静电复印机。 静电场的危害：静电感应引起高压电线对周围的影响。静电引发火灾，-静电防护。 3.1 静电场分析 本节内容 3.1.1 静电场的基本方程和边界条件 3.1.2 电位函数 3.1.3 导体系统的电容与部分电容 3.1.4 静电场的能量 3.1.5 静电力 3.1.1 静电场的基本方程和边界条件 1. 基本方程 微分形式      =  = E 0 D    积分形式       =  =   d 0 d E l D S     C S q D E 本构关系   =  2. 边界条件

e。D,-D)=ps D。-D2n=Ps e×(E,-E2)=0 E:-E21=0 若分界面上不存在面电荷，即P=0,则 介质1 个质2 e.(D,-D2)=0 ex(E,-E)=0 或 场矢量的折射关系 an8-E,/E2=/D。=5 tan 0,Ex/E2n 621D2m62 导体表面的边界条件 在静电平衡的情况下，导体内部的电场为0，则导体表面的边界条件为 [D=Ps (D=Ps En×E=0 或 E,=0 3.1.2电位函数 1.电位函数的定义 的 V×E=0>E=-V0 即静电场可以用一个标量函数的梯度来表示，标量函数称为静电场的标量电位或简称电位。 2.电位的表达式 对于连续的体分布电荷，由 R=F-T E(F)= 4πJh dV'= 4Ep(H =-X克叮 R 故得 )avc 1 同理得，面电荷的电位： 1exar+c 线电荷的电位： o)=4元cR

2      − =  − = ( ) 0 ( ) n 1 2 n 1 2 E E D D       e e  S 或    − = − = 1t 2t 0 1n 2n E E D D  S 若分界面上不存在面电荷，即 S = 0 ，则      − =  − = ( ) 0 ( ) 0 n 1 2 n 1 2 E E D D       e e 或    = = 1t 2t 1n 2n E E D D 场矢量的折射关系 2 1 2 2n 1 1n 2t 2n 1t 1n 2 1 / / / / tan tan       = = = D D E E E E 导体表面的边界条件 在静电平衡的情况下，导体内部的电场为 0，则导体表面的边界条件为      =  = n 0 n E D     e e  S 或    = = t 0 n E D  S 3.1.2 电位函数 1. 电位函数的定义 由  E = 0  E = −  即静电场可以用一个标量函数的梯度来表示，标量函数 称为静电场的标量电位或简称电位。 2. 电位的表达式 对于连续的体分布电荷，由 )d ] 1 ( )( 4π 1 [ )d 1 ( ) ( 4π 1 d ( ) 4π 1 ( ) 3 V R r V R V r R r R E r V V V = −    = −     =                故得 ( ) V C R r r V  +  =  d ( ) 4π 1      同理得，面电荷的电位： S C R r r S S +  =  d ( ) 4π 1 ( ) 3      线电荷的电位： ( ) l C R r r C l  +  =  d ( ) 4π 1      介质 2 介质 1 2  1   2 1 E2  E1  en  R = r − r     3 1 R R R   = −      

点电荷的电位： of)-+c 3.电位差 将E=-Vp两端点乘dl,则有 E-dJ-Vo-dj-(ddd)-dp dy av 上式两边从点P到点Q沿任意路径进行积分，得 Eidi=-do-P)-) 电场力做的功 P、Q两点间的电位差 关于电位差的说明 P、Q两点间的电位差等于电场力将单位正电荷从P点移至Q点所做的功，电场力使单位正电荷 由高电位处移到低电位处。 申位差也称为申压，可用U表示。 电位差有确定值，只与首尾两点位置有关，与积分路径无关。 4由位参考点 静电位不惟一，可以相差一个常数，即 0-p+C→Vp-(0+C)=7p 为使空间各点电位具有确定值，可以选定空间某一点作为参考点，且令参考点的电位为零，由 于空间各点与参考点的电位差为确定值，所以该点的电位也就具有确定值，即 选参考点 令参考点电位为零 电位确定值（电位差） 两点间电位差有定值 选择电位参考点的原则 ()应使电位表达式有意义。(3)同一个问题只能有一个参考点。 (2)应使电位表达式最简单。若电荷分布在有限区域，通常取无限远作电位参考点。 例3.1.1求电偶极子的电位

3 点电荷的电位： ( ) C R q r = +   4π  3. 电位差 将 E = −  两端点乘 l  d ，则有     d  d ( d d d ) = −d   +   +    = −  = − y y y y x x E l l    上式两边从点 P 到点 Q 沿任意路径进行积分，得 E dl d (P) (Q) Q P Q P  = −  = −    关于电位差的说明 P、Q 两点间的电位差等于电场力将单位正电荷从 P 点移至 Q 点所做的功，电场力使单位正电荷 由高电位处移到低电位处。 电位差也称为电压，可用 U 表示。 电位差有确定值，只与首尾两点位置有关，与积分路径无关。 4. 电位参考点 静电位不惟一，可以相差一个常数，即  = +C   = ( +C) =  为使空间各点电位具有确定值，可以选定空间某一点作为参考点，且令参考点的电位为零，由 于空间各点与参考点的电位差为确定值，所以该点的电位也就具有确定值，即 选择电位参考点的原则 (1)应使电位表达式有意义。(3)同一个问题只能有一个参考点。 (2)应使电位表达式最简单。若电荷分布在有限区域，通常取无限远作电位参考点。 例 3.1.1 求电偶极子的电位. 1 2 2 1 0 1 2 4π 0 ) 1 1 ( 4π ( ) rr q r r r r q r − = − =     电场力做的功 P、Q 两点间的电位差 选参考点 令参考点电位为零 电位确定值(电位差) 两点间电位差有定值

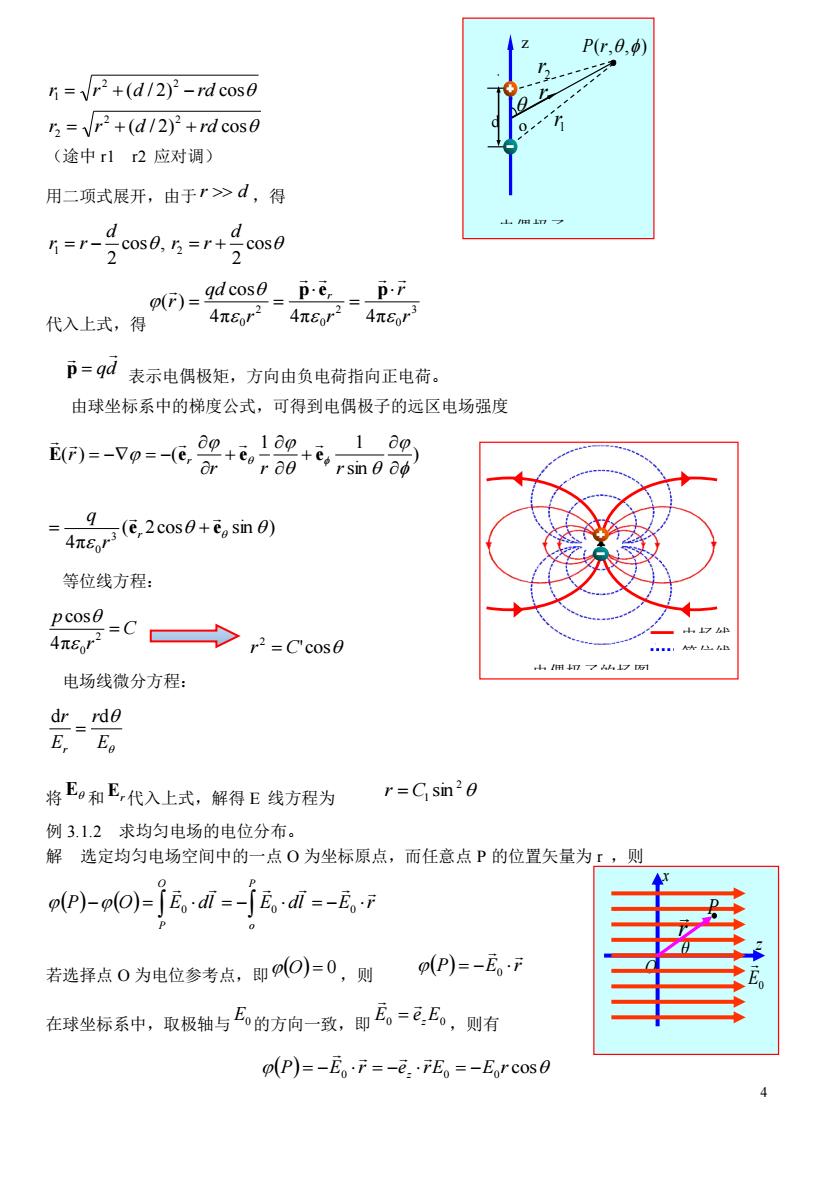
P(r.0.0 片=Vr2+(d/2)2-rd cos8 +(d/2)+rdcos0 (途中r12应对调) 用二项式展开，由于r>d,得 d 山mn一 =r-号m85=r+号ow0 代入上式，得 n恶 D=9d表示电偶极矩，方向由负电荷指向正电荷： 由球坐标系中的梯度公式，可得到电偶极子的远区电场强度 1a0 -4ze2os0+8,sm0) 等位线方程： pcos0 4C→，=Cs0 电场线微分方程： d业_d0 E Eo 将E0和E,代入上式，解得E线方程为 r=C sin20 例3.12求均匀电场的电位分布。 解选定均匀电场空间中的一点0为坐标原点，而任意点P的位置矢量为r,则 pp)-po)=fE,di=-a。d=-E元 若选择点0为电位参考点，即O)=0,则 (P=-E·F 在球坐标系中，取极轴与瓦的方向一致，即瓦。=.E。,则有 p(P)=-E。·F=-e.·E。=-Ercos0

4   ( / 2) cos ( / 2) cos 2 2 2 2 2 1 r r d rd r r d rd = + + = + − （途中 r1 r2 应对调） 用二项式展开，由于 r  d ，得 cos , 2 1  d r = r − cos 2 2 d r = r + 代入上式，得 3 0 2 0 2 4π 0 4π 4π cos ( ) r r r r qd r r            =  = = p e p qd   p = 表示电偶极矩，方向由负电荷指向正电荷。 由球坐标系中的梯度公式，可得到电偶极子的远区电场强度 ) sin 1 1 ( ) (            +   +   = − = − r r r r r E e e e      ( 2cos sin ) 4π 3 0     e e   = r + r q 等位线方程： C r p = 2 4π 0 cos   'cos 2 r = C 电场线微分方程：   E r E r r d d = 将 E 和 Er 代入上式，解得 E 线方程为  2 1 r = C sin 例 3.1.2 求均匀电场的电位分布。 解 选定均匀电场空间中的一点 O 为坐标原点，而任意点 P 的位置矢量为 r ，则 (P) (O) E dl E dl E r P o O P       − =  = −  = −     0  0 0 若选择点 O 为电位参考点，即 (O) = 0 ，则 (P) E r   = −   0 在球坐标系中，取极轴与 E0 的方向一致，即 0 E0 E ez   = ，则有 (P) = −E0 r = −ez rE0 = −E0 r cos      + q 电偶极子 z d o － q 1 r 2 r r P(r,,) 等位线 电场线 电偶极子的场图 E0  x  z O P r 

在圆柱坐标系中，取瓦与x轴方向一致，即E,=,而=，P+区：，故 p(P)=-E。·F=-e·Eenp+e.)=-Eopcos 例3.1.3求长度为2L、电荷线密度为P0的均匀带电线的电位。 解采用圆柱坐标系，令线电荷与z轴相重合，中点位于坐标原点。由于轴对称性，电位与无 关，在带电线上位于：处的线元d=正，它到点P0、女、)的距离R=D+(-),则 F)=P。r」 1 p+-出 -++-] d/'=d=' =mhp+-F-) 46p2+6+L-(+) 在上式中若令L→0，则可得到无限长直线电荷的电位。当L>R时，上武可写为 s会hD+正+'=ahD+E+L.h2马 4π6 P+-L 46 p 2π6p 当L→∞时，上式变为无穷大，这是因为电荷不是分布在有限区域内，而将电位参考点选在无穷 远点之故。这时可在上式中加上一个任意常数，则有 会兴c 并选择有限远处为电位参考点。例如，选择p=a的点为电位参考点，则有 C=2L 26atf)=,h4 2π6p 5.电位的微分方程 在均匀介质中，有 ,1标量泊松方程 V.D=p-V.E=p/s E=-V0 V'o=-pls 在无源区城，p=0→☑0=0.拉普拉斯方程

5 在圆柱坐标系中，取 E0  与 x 轴方向一致，即 0 E0 E ex   = ，而 r e e zz    =  + ，故 (P) = −E0 r = −ex  E0 (e + ez z) = −E0 cos      例 3.1.3 求长度为 2L、电荷线密度为 l0 的均匀带电线的电位。 解 采用圆柱坐标系，令线电荷与 z 轴相重合，中点位于坐标原点。由于轴对称性，电位与  无 关。在带电线上位于 z  处的线元 dl = dz  ，它到点 p(、、z) 的距离 ( ) 2 2 R =  + z − z  ，则 ( ) ( ) ( ) ( ) ( ) (z L) (z L) z L z L z z z z dz z z r l L L l L L l + + − + + − − − =     =  − + + −   + −   = − − 2 2 2 2 0 0 2 2 0 0 2 2 0 0 ln 4 ln | 4 1 4                在上式中若令 L →  ，则可得到无限长直线电荷的电位。当 L  R 时，上式可写为 ( )                L L L L L L L r l l l 2 ln 2 ln 4 ln 4 0 0 2 2 0 0 2 2 2 2 0 0  + + = + − + +   当 L →  时，上式变为无穷大，这是因为电荷不是分布在有限区域内，而将电位参考点选在无穷 远点之故。这时可在上式中加上一个任意常数，则有 ( ) C L r l = +      2 ln 2 0 0  并选择有限远处为电位参考点。例如，选择ρ= a 的点为电位参考点，则有 a L C l 2 ln 2 0 0   = ( )     a r l ln 2 0 0 =  5. 电位的微分方程 在均匀介质中，有     = −  =   =     E D E      = −   2 在无源区域，  = 0 0 2   = x y z L - L ( , , )   z z' d d l z   = R 标量泊松方程 拉普拉斯方程

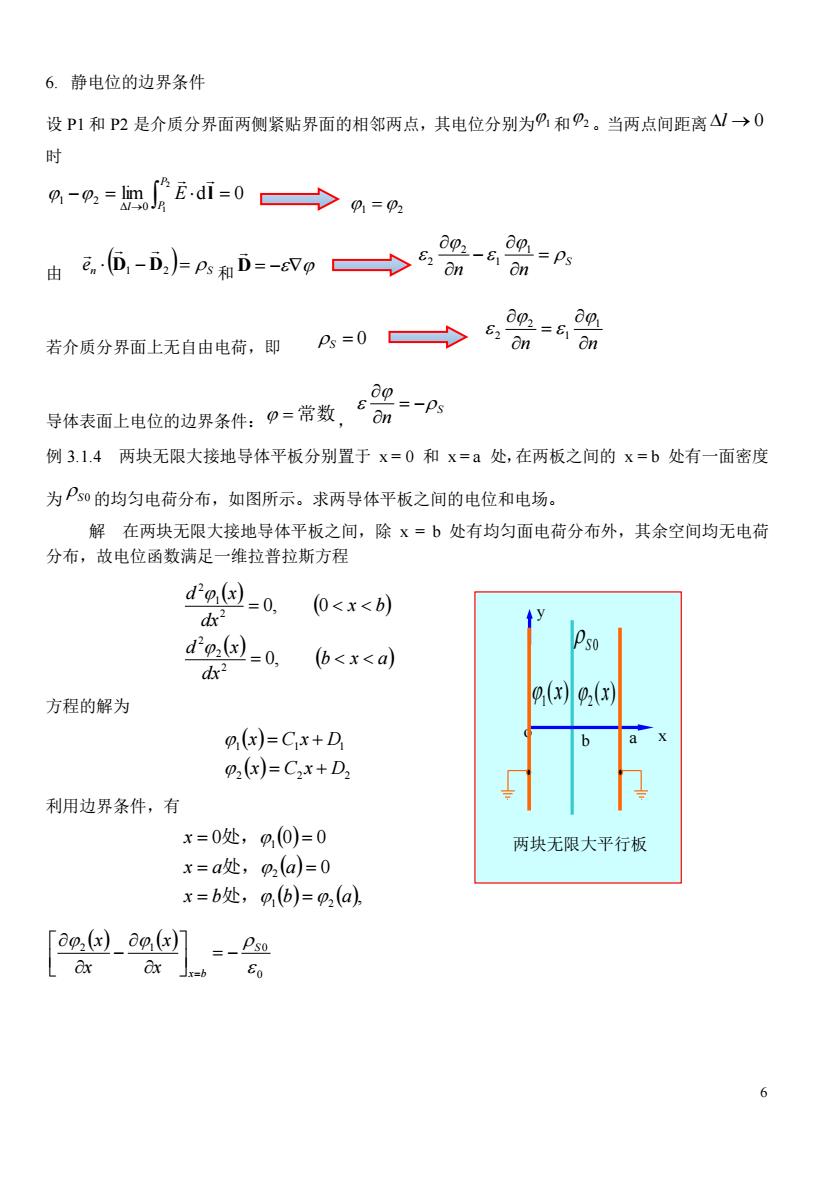
6.静电位的边界条件 设P1和P2是介质分界面两侧紧贴界面的相邻两点，其电位分别为9和9？。当两点间距离△1→0 时 %-%=mE.d=0→0=0 若介质分界面上无自由电荷，即 A-0>6需=6器 =-p 导体表面上电位的边界条件：p=常数，m 例3.1.4两块无限大接地导体平板分别置于x=0和x=a处，在两板之间的x=b处有一面密度 为Ps0的均匀电荷分布，如图所示。求两导体平板之间的电位和电场。 解在两块无限大接地导体平板之间，除x=b处有均匀面电荷分布外，其余空间均无电荷 分布，故电位函数满足一维拉普拉斯方程 do()-0. (0<x<b) dx y do:(x)-0. (b<x<a) dx 方程的解为 0(x0(x) o(x)=Cx+D 2(x)=C2x+D2 利用边界条件，有 x=0处，%，0)=0 两块无限大平行板 x=a处，p2(a)=0 x=b处，0，(b)=p(a 「a9.d_agd=-

6 6. 静电位的边界条件 设 P1 和 P2 是介质分界面两侧紧贴界面的相邻两点，其电位分别为 1 和 2 。当两点间距离 l → 0 时 lim d 0 2 Δ 0 1 1 − 2 =  = →  P l P E l     1 =2 由 ( ) n S e  D1 − D2 =     和 D = −  S n n      =   −   1 1 2 2 若介质分界面上无自由电荷，即 S = 0 n n  =   1 1 2 2     导体表面上电位的边界条件：  = 常数， S n    = −   例 3.1.4 两块无限大接地导体平板分别置于 x = 0 和 x = a 处，在两板之间的 x = b 处有一面密度 为 S 0 的均匀电荷分布，如图所示。求两导体平板之间的电位和电场。 解 在两块无限大接地导体平板之间，除 x = b 处有均匀面电荷分布外，其余空间均无电荷 分布，故电位函数满足一维拉普拉斯方程 ( ) ( ) ( ) (b x a) dx d x x b dx d x =   =   0, 0, 0 2 2 2 2 1 2   方程的解为 ( ) ( ) 2 2 2 1 1 1 x C x D x C x D = + = +   利用边界条件，有 ( ) ( ) ( ) ( ), 0 0 0 0 1 2 2 1 x b b a x a a x     = = = = = = 处， 处， 处， ( ) ( ) 0 2 1 0     S x b x x x x = −         −   = o b a x y 两块无限大平行板 S 0  1  ( ) x 2  ( ) x

所以D,=0 C3a+D2=0 Cb+D=Cb+D: 最后得 C:-C=-Pso 60 n)=la-lx0sxs） oa 由此解得 9()-Pxb(a-x)(bsxsa) Eoa C=-2su(6-a) D=0 E(*)-Vg.(r)-2,esola-b) C:=-Poob,D.=exb E.(x)=-Vo.(x)-i.Pxb Sa 3.1.3导体系统的电容与部分电容 (1)在电子电路中，利用电容器来实现滤波、移相、隔直、旁路、选频等作用。 (2)通过电容、电感、电阻的排布，可组合成各种功能的复杂电路。 (3)在电力系统中，可利用电容器来改善系统的功率因数，以减少电能的损失和提高电气设备的 利用率。 1.电容 电容是导体系统的一种基本属性，是描述导体系统储存电荷能力的物理量。孤立导体的电容，孤 C-9 立导体的电容定义为所带电量q与其电位P的比值，即 ?两个带等量异号电荷（±q)的导 9 体组成的电容器，其电容为 电容的大小只与导体系统的几何尺寸、形状和及周围电介质的特性参数有关，而与导体的带电 量和电位无关。 计算申容的方法一： 山假定两导体上分别带申荷如和 计算电容的方法二： 山)假定两申极间的电位差为U: 一q: (2)计算两导体间的电场强度E: (2)计算两电极间的电位分布P: B由-矿E,、求出西生如 )由E=-Vp符到E 的电位差： ④求比值C=9/心，即得出所求电 ④由A=E,得到P q=p,ds (⑤由 ,求出导体的电苞

7 0 0 2 1 1 1 2 2 2 2 1 0 0   S C C C b D C b D C a D D − = − + = + + = 所以 = ( ) 0 0 2 0 0 2 1 0 0 1 , , 0       b D a b C D b a C S S S = − = = − = − 由此解得 3.1.3 导体系统的电容与部分电容 （1）在电子电路中，利用电容器来实现滤波、移相、隔直、旁路、选频等作用。 （2）通过电容、电感、电阻的排布，可组合成各种功能的复杂电路。 （3）在电力系统中，可利用电容器来改善系统的功率因数，以减少电能的损失和提高电气设备的 利用率。 1. 电容 电容是导体系统的一种基本属性，是描述导体系统 储存电荷能力的物理量。孤立导体的电容，孤 立导体的电容定义为所带电量 q 与其电位  的比值，即  q C = 两个带等量异号电荷（  q ）的导 体组成的电容器，其电容为 1 −2 = = q U q C 电容的大小只与导体系统的几何尺寸、形状和及周围电介质的特性参数有关，而与导体的带电 量和电位无关。 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) a b E x x e a a b E x x e a x b x a a b x x x b a a b x S x S x S S 0 0 2 2 0 0 1 1 0 0 2 0 0 1 , , 0                 = − = − = − = − = −     − = 最后得 计算电容的方法二： (1) 假定两电极间的电位差为 U ； (2) 计算两电极间的电位分布  ； (3) 由 E = −  得到 E ; (4) 由 S En  =  得到  S ; (5) 由 q dS s =   s ，求出导体的电荷 q ； (6) 求比值 ，即得出所求电 容。 计算电容的方法一： (1) 假定两导体上分别带电荷+q 和 －q ； (2) 计算两导体间的电场强度 E； (3) 由  =  2 1 U E dl   ，求出两导体间 的电位差； (4) 求比值 C = q U ，即得出所求电 容

9=☑ =0 例3.1.4同心球形电容器的内导体半径为a、外导体半径为b,其间填充介电常数为的均匀介质 求此球形电容器的电容。 解：设内导体的电荷为q,则由高斯定理可求得内外导体间的电场 D=g,E=6,4怀g 同心导体间的电压 u-品启》品品 C=4=4TEab 球形电容器的电容 U b-a -一一孤立导体球的电容 当6→时，C=4标0← 例3.15如图所示的平行双线传输线，导线半径为a,两导线的轴线距离为D,且D>a,求 传输线单位长度的电容。 解设两导线单位长度带电量分别为十P和一P。由于D>a,故可近似地认为电荷分别均匀分布 在两导线的表面上。应用高斯定理和叠加原理，可得到两导线之间的平面上任一点 P的电场强度为 )=,1 1 2π6（xD-x 两导线间的电位差 a- π6

8 例 3.1.4 同心球形电容器的内导体半径为 a 、外导体半径为 b，其间填充介电常数为ε的均匀介质。 求此球形电容器的电容。 解：设内导体的电荷为 q ，则由高斯定理可求得内外导体间的电场 2 2 4 , 4 r q E e r q D er r        = = 同心导体间的电压 ab q b a a b q U Edr b a −  =       = = −  0 4 0 1 1 4    球形电容器的电容 b a ab U q C − = = 40 当b →时，C = 40a 例 3.1.5 如图所示的平行双线传输线，导线半径为 a ，两导线的轴线距离为 D ，且 D >> a ，求 传输线单位长度的电容。 解 设两导线单位长度带电量分别为 + l 和 − l 。由于 D  a ，故可近似地认为电荷分别均匀分布 在两导线的表面上。应用高斯定理和叠加原理，可得到两导线之间的平面上任一点 P 的电场强度为 ( )       − = + x D x E x e l x 1 1 2  0    两导线间的电位差 a D a dx x D x U E dl l D a a l −  =      − =  = +   − ln 1 1 2 0 0 2 1          E  2 = 0 1 =U + q − q 孤立导体球的电容 x y z x D a

故单位长度的电容为 G-号-o-aya"n(pia π6 π6 (F/m) 例3.1.6同轴线内导体半径为，外导体半径为b,内外导体间填充的介电常数为6的均匀介质， 求同轴线单位长度的电容。 解设同轴线的内、外导体单位长度带电量分别为P和一P,应用高斯定理可得到内外导体间任 一点的电场强度为 ip）=E,2rp 内外导体间的电位差 同轴线 =Ph(b/a) 2π 故得同轴线单位长度的电容为 2π8 U-h(bla)(F/m) *2.部份电容 在多导体系统中，任何两个导体间的电压都要受到其余导体上的电荷的影响。因此，研究多导体系 统时，必须把电容的概念加以推广，引入部分电容的概念。 (1)电位系数 由N个导体组成的系统中，由于电位与各导体所带的电荷之间成线性关系，所以，各导体的电位 为 月-2ag,6=2,州 式中：a0=1,2,.N)-自电位系数 a,(≠)-互电位系数 电位系数的特点： （1)a,在数值上等于第i个导体上的总电量为一个单位、而其余导体上的总电量都为零时，第j 个导体上的电位，即 a,=21g,==9.=9.9w=06j=12,N)

9 故单位长度的电容为 ( )  ( ) (F m) U D a a D a C l ln ln 0 0 1       − = = 例 3.1.6 同轴线内导体半径为 a ，外导体半径为 b ，内外导体间填充的介电常数为  的均匀介质， 求同轴线单位长度的电容。 解 设同轴线的内、外导体单位长度带电量分别为 + l 和 − l ，应用高斯定理可得到内外导体间任 一点的电场强度为 ( )     2 l E e   = 内外导体间的电位差 ( ) (b a) U E e d d l b a l b a ln 2 1 2            = =  =     故得同轴线单位长度的电容为 ( ) (F m) U b a C l ln 2 1    = = ＊ 2. 部份电容 在多导体系统中，任何两个导体间的电压都要受到其余导体上的电荷的影响。因此，研究多导体系 统时，必须把电容的概念加以推广，引入部分电容的概念。 （1） 电位系数 在由 N 个导体组成的系统中，由于电位与各导体所带的电荷之间成线性关系，所以，各导体的电位 为 q (i N) j N j i ij 1,2, , 1 =  =  =   ( ) ( ) 互电位系数 式中： 自电位系数  − − − = − − − i j i N ij ij   1,2, 电位系数的特点： （1） ij 在数值上等于第 i 个导体上的总电量为一个单位、而其余导体上的总电量都为零时，第 j 个导体上的电位，即 q q q q (i j N) q j j N j i i j | 0 , 1,2, , = 1 == −1= +1 = =     a b 同轴线

(2)a只与各导体的形状、尺寸、相互位置以及导体周围的介质参数有关，而与各导体的电位和 带电量无关： 64y>0. (4)具有对称性，即Q,=0m。 (2)电容系数 若己知各导体的电位，则各导体的电量可表示为 g=立%=12，N 式中：B=1,2,.,N)-自电容系数或自感应系数 B(≠)-互电容系数或互感应系数 电容系数的特点： (1)B,在数值上等于第j个导体上的电位为一个单位、而其余导体接地时，第i个导体上的电 量，即 B,=g1A==9=9m=9w=06j=12,. (2)B订j只与各导体的形状、尺寸、相互位置以及导体周围的介质参数有关，而与各导体的电位 和带电量无关： (3)B>0、B,≤0f≠方 (4)具有对称性，即B≠B。 (3)部分电容 将各导体的电量表示为 9,=∑P9,=∑B,0,-B,A+R,A)=-∑B,Q-p,+∑B,A =∑C,-9,+C06=l2., 式中：C=-B,6≠) 一一导体i与导体j之间的部分电容

10 （2） ij 只与各导体的形状、尺寸、相互位置以及导体周围的介质参数有关，而与各导体的电位和 带电量无关； (3) ij  0 ； (4)具有对称性，即 ij = aji 。 （2） 电容系数 若已知各导体的电位，则各导体的电量可表示为 q (i N) N j i ij j 1,2, , 1 =  =  =   ( ) ( ) 互电容系数或互感应系数 式中： 自电容系数或自感应系数  − − − = − − − i j i N i j i j   1,2,, 电容系数的特点： （1） ij 在数值上等于第 j 个导体上的电位为一个单位、而其余导体接地时，第 i 个导体上的电 量，即 (i j N) q j j N j i i j | 0 , 1,2, , = 1 == −1 = +1= = =    （2）βi j 只与各导体的形状、尺寸、相互位置以及导体周围的介质参数有关，而与各导体的电位 和带电量无关； （3） 0 0(i j); ii  、ii   （4）具有对称性，即 ij   ji 。 （3） 部分电容 将各导体的电量表示为 ( ) ( ) C ( ) C (i N) q i i i N j i i j i j N j i j i N j i i j i j N j j i j j i j i i j i N j i i j 1,2, , 1 1 1 = − + =  = = − + = − − +       = =  =                 式中： C (i j) ij = −ij  —— 导体 i 与导体 j 之间的部分电容