
鲜电雕 2005-1-25 第一章电磁场的数学物理基础
2005-1-25 第一章 电磁场的数学物理基础 1

·本章讨论内容 2.1电荷守恒定律 2.2真空中静电场的基本规律 2.3真空中恒定磁场的基本规律 2.4媒质的电磁特性 2.5 电磁感应定律和位移电流 2.6麦克斯韦方程组 2.7 电磁场的边界条件 2005-1-25 第章电磁场的数学物理基础
2005-1-25 第一章 电磁场的数学物理基础 2 2.1 电荷守恒定律 2.2 真空中静电场的基本规律 2.3 真空中恒定磁场的基本规律 2.4 媒质的电磁特性 2.5 电磁感应定律和位移电流 2.6 麦克斯韦方程组 2.7 电磁场的边界条件 • 本章讨论内容

2.11 申电荷守恒定律 电磁场物理模型中的基本理量句分为原童和防量两大类。 源量为电荷q(和电流 1(,)分别用来描述产生电磁效应 的两类场源。电荷是产生电场的源,电流是产生磁场的源。 电荷 →电流 ↓ (运动) ↓ 电场 磁场 2005-1-25 第一章电磁场的数学物理基础 >
2005-1-25 第一章 电磁场的数学物理基础 3 电磁场物理模型中的基本物理量可分为源量和场量两大类 2.1 电荷守恒定律 。 电荷 电流 电场 磁场 (运动) 源量为电荷 和电流 ,分别用来描述产生电磁效应 的两类场源。电荷是产生电场的源,电流是产生磁场的源。 q(r ,t) I(r ,t)

本节内容 2.1.1电荷与电荷密度 2.1.2电流与电流密度 2.1.3电荷守恒定律 2005-1-25 第一章电磁场的数学物理基础 网>I
2005-1-25 第一章 电磁场的数学物理基础 4 本节内容 2.1.1 电荷与电荷密度 2.1.2 电流与电流密度 2.1.3 电荷守恒定律

2.1.1电荷与电荷密度 。电荷是物质基本属性之一。 ·1897年英国科学家汤姆逊(J.J.Thomson)在实验中发现了 电子。 。1907一1913年间,美国科学家密立根(R.A.Miliken)通过 油滴实验,精确测定电子电荷的量值为 e=1.60217733×10-19 (单位:C) 确认了电荷的量子化概念。换句话说,是最小的电荷,而任 何带电粒子所带电荷都是ε的整数倍。 ·宏观分析时,电荷常是数以亿计的电子电荷的集合,故 可不考虑其量子化的事实,而认为电荷量可任意连续取值。 2005-1-25 第一章电磁场的数学物理基础
2005-1-25 第一章 电磁场的数学物理基础 5 • 电荷是物质基本属性之一。 • 1897年英国科学家汤姆逊(J.J.Thomson)在实验中发现了 电子。 • 1907 — 1913年间,美国科学家密立根(R.A.Miliken)通过 油滴实验,精确测定电子电荷的量值为 e =1.602 177 33×10-19 (单位:C ) 确认了电荷的量子化概念。换句话说,e 是最小的电荷,而任 何带电粒子所带电荷都是e 的整数倍。 • 宏观分析时,电荷常是数以亿计的电子电荷e的集合,故 可不考虑其量子化的事实,而认为电荷量q可任意连续取值。 2.1.1 电荷与电荷密度
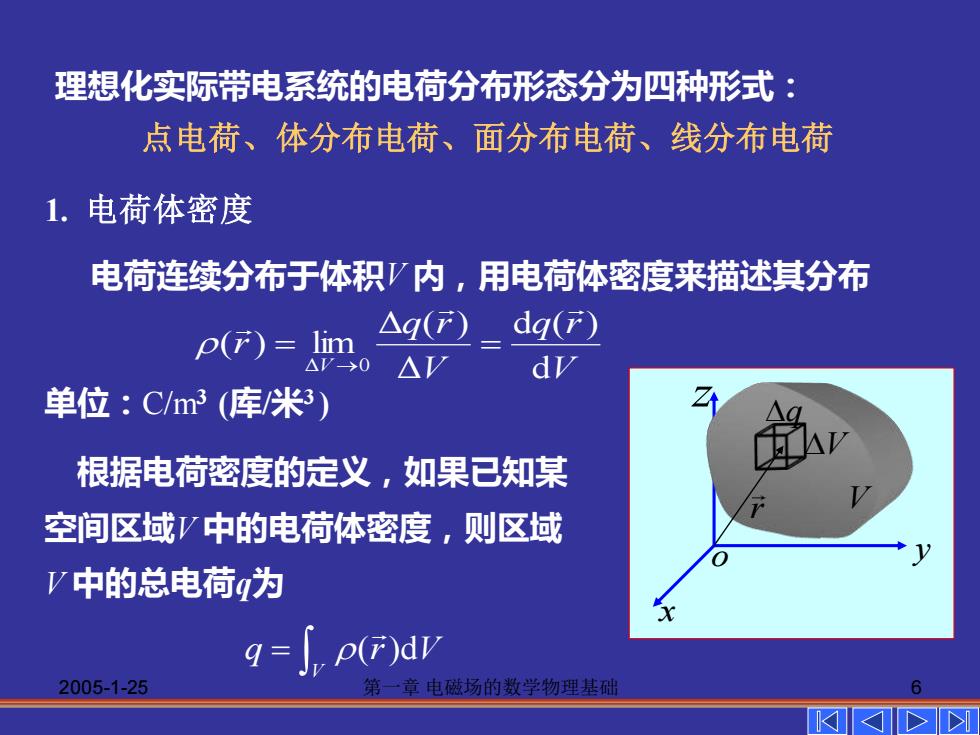
理想化实际带电系统的电荷分布形态分为四种形式: 点电荷、体分布电荷、面分布电荷、线分布电荷 1.电荷体密度 电荷连续分布于体积V内,用电荷体密度来描述其分布 P(r)=lim △q(F)dqF) △r0△V 单位:C/m3(库/米3) 根据电荷密度的定义,如果已知某 空间区域V中的电荷体密度,则区域 V中的总电荷为 q=],p(F)dv 2005-1-25 第一章电磁场的数学物理基础 6
2005-1-25 第一章 电磁场的数学物理基础 6 1. 电荷体密度 V q r V q r r V d d ( ) Δ Δ ( ) ( ) lim Δ 0 = = → = V q (r)dV 单位:C/m3 (库/米3 ) 根据电荷密度的定义,如果已知某 空间区域V 中的电荷体密度,则区域 V 中的总电荷q为 电荷连续分布于体积V 内,用电荷体密度来描述其分布 理想化实际带电系统的电荷分布形态分为四种形式: 点电荷、体分布电荷、面分布电荷、线分布电荷 q V y x z o r V

2.电荷面密度 若电荷分布在薄层上,当仅考虑薄层外、距薄层的距离要 比薄层的厚度大得多处的电场,而不分析和计算该薄层内的电 场时,可将该薄层的厚度忽略,认为电荷是面分布。面分布的 电荷可用电荷面密度表示。 ps()=lim △q(T) dq(r) △S→0△S dS AS Aq 单位:C/m2(库/米2) 如果已知某空间曲面S上的电荷面 密度,则该曲面上的总电荷(为 q=J P.(F)dS 2005-1-25 第一章电磁场的数学物理基础
2005-1-25 第一章 电磁场的数学物理基础 7 若电荷分布在薄层上,当仅考虑薄层外、距薄层的距离要 比薄层的厚度大得多处的电场,而不分析和计算该薄层内的电 场时,可将该薄层的厚度忽略,认为电荷是面分布。面分布的 电荷可用电荷面密度表示。 2. 电荷面密度 单位: C/m2 (库/米2 ) 如果已知某空间曲面S 上的电荷面 密度,则该曲面上的总电荷q 为 = S s q (r)dS S q r S q r r S S d d ( ) Δ Δ ( ) ( ) lim Δ 0 = = → y x z o r S q S

3.电荷线密度 若电荷分布在细线上,当仅考虑细线外、距细线的距离要 比细线的直径大得多处的电场,而不分析和计算线内的电场时, 可将线的直径忽略,认为电荷是线分布。线分布的电荷可用电 荷线密度表示。 e()=lim △q)_dq(F) △/>0 △1 dl 单位:C/m(库/米) 如果已知某空间曲线上的电荷线 密度,则该曲线上的总电荷q为 p()di 2005-1-25 第一章电磁场的数学物理基础 8
2005-1-25 第一章 电磁场的数学物理基础 8 若电荷分布在细线上,当仅考虑细线外、距细线的距离要 比细线的直径大得多处的电场,而不分析和计算线内的电场时, 可将线的直径忽略,认为电荷是线分布。线分布的电荷可用电 荷线密度表示。 3. 电荷线密度 l q r l q r r l l d d ( ) Δ Δ ( ) ( ) lim Δ 0 = = → 如果已知某空间曲线上的电荷线 密度,则该曲线上的总电荷q 为 = C l q (r)dl 单位: C / m (库/米) y x z o r q l

4.点电荷 将电荷量g想象集中在几何点上。 理论分析电磁场时此概念非常重要。 对于总电荷为q的电荷集中在很小区域V的情况,当不分析 和计算该电荷所在的小区域中的电场,而仅需要分析和计算电 场的区域又距离电荷区很远,即场点距源点的距离远大于电荷 所在的源区的线度时,小体积V中的电荷可看作位于该区域中 心、电荷为q的点电荷。 点电荷的电荷密度表示 p()=qδ(f-' 2005-1-25 第一章电磁场的数学物理基
2005-1-25 第一章 电磁场的数学物理基础 9 对于总电荷为 q 的电荷集中在很小区域 V 的情况,当不分析 和计算该电荷所在的小区域中的电场,而仅需要分析和计算电 场的区域又距离电荷区很远,即场点距源点的距离远大于电荷 所在的源区的线度时,小体积 V 中的电荷可看作位于该区域中 心、电荷为 q 的点电荷。 点电荷的电荷密度表示 (r) = qδ(r − r ) 4. 点电荷 y x z o r q 将电荷量q想象集中在几何点上。 理论分析电磁场时此概念非常重要

2.1.2 电流与电流密度 电流一电荷的定向运动而形成,用表示,其大小定义为: 单位时间内通过某一横截面S的电荷量,即 i=lim(△q/△t)=dq/dt 单位:A(安)》 电流方向:正电荷的流动方向 形成电流的条件: ·存在可以自由移动的电荷: 。存在电场。 说明:电流通常是时间的函数,不随时间变化的电流称为恒定 电流,用表示。 2005-1-25 第一章电磁场的数学物理基础 10
2005-1-25 第一章 电磁场的数学物理基础 10 2.1.2 电流与电流密度 说明:电流通常是时间的函数,不随时间变化的电流称为恒定 电流,用I 表示。 • 存在可以自由移动的电荷; • 存在电场。 单位: A (安) 电流方向: 正电荷的流动方向 0 lim ( ) d d t i q t q t → = = 电流 —— 电荷的定向运动而形成,用i 表示,其大小定义为: 单位时间内通过某一横截面S 的电荷量,即 形成电流的条件: