《电磁场理论》课程电子教案（讲义）第一章 矢量分析

场论 电磁场理论的主要研究领域 电磁场理论 电磁场理论发展历史 三大类应用问题 电磁场理论的主要研究领域 1.作为理论物理学的一个重要研究分支，主要致力于统一场理论和徽观量子电动力学的研究。 2作为无线电技术的理论基础，集中于三大类应用问愿的研究 二电磁场理论 电磁学：麦克斯韦方程组的积分形式。它概括了全部已有的宏观电磁现象的实验事实，给出 了用积分量描述宏观电磁场的全部规律。 电磁场理论：麦克斯韦方程组的徽分形式。是在电磁学的基础上，进一步研究宏观电磁现象 和电磁过程的基本规律及其计算方法的理论，是用数学方法描述空间任意一点、任意时刻电 磁现象变化规律的理论。 .nd-10.98 VxHi-J.0D at 及-要s 5B.d=0 V.B=0 f.D.ds-pdv V.D=p Maxwell方程组的物理意义 1这两个方程左边物理量为磁或电)，而右边物理量则为电（或磁）。这中间的等号深刻揭示了 电与磁的相互转化，相互依赖，相互对立，共存于统一的电磁波中。正是由于电不断转换为 磁，而磁又不断转成为电，才会发生能量交换和贮存。 2.进一步研究Maxwel方程两边的运算，从物理上看，运算反映一种作用(Action.方程的左 边是空间的运算旋度)：方程的右边是时间的运算（得数），中间用等号连接。它深刻揭示了电 (或磁)场任一地点的变化会转化成磁或电)场时间的变化：反过来，场的时间变化也会转化成 地点变化。正是这种空间和时间的相互变化构成了波动的外在形式。用通俗的一句话来说， 即一个地点出现过的事物，过了一段时间又在另一地点出现了。 3.Maxwell方程还指出：电磁转化有一个重要条件，即频率。让我们写出单色波颍域的 Maxwell 只有较或者说任何形式的信号高频分量都包含很少高的，才能确保电磁的有效转换，直流 情况没有转换。可以这样说，在高频时封闭电略才有可能变成开放电略。不过很有意思的是

场论 电磁场理论的主要研究领域 电磁场理论 电磁场理论发展历史 三大类应用问题 一，一、电磁场理论的主要研究领域 1.作为理论物理学的一个重要研究分支，主要致力于统一场理论和微观量子电动力学的研究。 2 作为无线电技术的理论基础，集中于三大类应用问题的研究。 二.电磁场理论 电磁学：麦克斯韦方程组的积分形式。它概括了全部已有的宏观电磁现象的实验事实，给出 了用积分量描述宏观电磁场的全部规律。 电磁场理论：麦克斯韦方程组的微分形式。是在电磁学的基础上，进一步研究宏观电磁现象 和电磁过程的基本规律及其计算方法的理论，是用数学方法描述空间任意一点、任意时刻电 磁现象变化规律的理论。 Maxwell 方程组的物理意义 1.这两个方程左边物理量为磁(或电)，而右边物理量则为电(或磁)。这中间的等号深刻揭示了 电与磁的相互转化，相互依赖，相互对立，共存于统一的电磁波中。正是由于电不断转换为 磁，而磁又不断转成为电，才会发生能量交换和贮存。 2.进一步研究 Maxwell 方程两边的运算，从物理上看，运算反映一种作用(Action)。方程的左 边是空间的运算(旋度)；方程的右边是时间的运算(导数)，中间用等号连接。它深刻揭示了电 (或磁)场任一地点的变化会转化成磁(或电)场时间的变化；反过来，场的时间变化也会转化成 地点变化。正是这种空间和时间的相互变化构成了波动的外在形式。用通俗的一句话来说， 即一个地点出现过的事物，过了一段时间又在另一地点出现了。 3. Maxwell 方程还指出：电磁转化有一个重要条件，即频率ω。让我们写出单色波频域的 Maxwell 只有较或者说任何形式的信号高频分量都包含很少高的ω，才能确保电磁的有效转换，直流 情况没有转换。可以这样说，在高频时封闭电路才有可能变成开放电路。不过很有意思的是             =  =     = −     = +        S V S C S C S D S ρdV B S S t B E l S t D H l J              d d 0 d d d ( ) d            =   =    = −    = + D B t B E t D H J        0

频率愈高，越难出功率，这也是一个有趣的矛盾。 三、电磁场理论发展历史 最初，人们只能定性观察电现象、磁现象 电磁场理论发展中的重大事件： 库仑定律（电荷相互作用力规律） 1820:电流微效应（奥斯特） 安培力定律（安培） 1831:电磁感应（法拉第） 1864:位移电流假说，麦克斯韦方程组（麦克斯韦） 1888:试验证明电磁波存在（赫兹） 电磁场理论的应用和发展 1887年，德国科学家赫兹用火花隙激励一个环状天线，用另一个带隙的环状天线接收， 证实了麦克斯韦关于电磁波存在的预言，这一重要的实验导致了后来无线电报的发明。从此 开始了电磁场理论应用与发展时代，并且发展成为当代最引人注目的学科之一。 无线电报1895年，意大利马可尼成功地进行了 2.5公里距离的无线电报传送实验。1896年，波波夫进行了约250米距离的类似试验 1899年，无 线电报跨越英吉利海峡的试验成功：1901年，跨越大西洋的3200公里距 离的试验成功。马可尼以其在无线电报等领域的成就，获得了1909年的诺贝尔奖金物 理学奖。无线电报的发明，开始了利用电磁波时期。 有线电话 1876年美国A.G.贝尔在美国建国 100周年博览会上展示了他所发明 的有线电话。 此后，有线电话便迅速普及开来。 雷达(Radio Detection and Ranging) 二次世界大战前夕，飞机成为主要进攻武器。英、美、德、法等国竞相研制一类能够早期警 戒飞机的装置。1936年，英国的瓦特设计的警戒留达最先投入了运行。有效地警戒了来自德 国的轰炸机。1938年，美国研制成第一部能指挥火炮射击的火炮控制雷达。1940年，多腔磁 控管的发明，徽波雷达的研制成为可能。194年，能够自动跟踪飞机的雷达研制成功。1945 年，能消除背景干扰显示运动目标的显示技术的发明，使雷达更加完善。在整个第二次世界大 战期间，雷达成了电磁场理论最活跃的部分。卫星通信技术1958年，美国发射低轨的“斯科 尔”卫星成功，这是第一颗用于通信的试验卫星。1964年，借助定点同步通信卫星首次实现了 美、欧、非三大洲的通信和电视转播。1965年，第一颗商用定点同步卫星投入运行。1969年， 大西洋、太平洋和印度洋上空均已有定点同步通信卫星，卫星地球站已遍布世界各国，这些卫 星地球站又和本国或本地区的通信网接通。卫星通信经历10年的发展，终趋于成熟。 卫星定位技术1957年卫星发射成功后，人们试图将雷达引入卫星，实现以卫星为基地 对地球表面及近地空间目标的定位和导航。1958年底，美国开始研究实施这一计划， 于1964年研究成功子午仪卫星导航系统。1973年美国提出了由24颗卫星组成的实用系 统新方案，即GPS计划。它是英文 Navigation Satellite Timing and Ranging /Global Positioning System的字头缩写NAVSTAR/GPS的简称，其含义是利用导航卫星进 行测时和测距。1990年最终的GS方案是由21颗工作卫星和3颗在轨备用卫星组成。 三三大类应用问题：

频率愈高，越难出功率，这也是一个有趣的矛盾。 三、电磁场理论发展历史 最初，人们只能定性观察电现象、磁现象 电磁场理论发展中的重大事件： 库仑定律（电荷相互作用力规律） 1820：电流磁效应（奥斯特） 安培力定律（安培） 1831：电磁感应（法拉第） 1864：位移电流假说，麦克斯韦方程组(麦克斯韦) 1888：试验证明电磁波存在（赫兹） 电磁场理论的应用和发展 1887 年，德国科学家赫兹用火花隙激励一个环状天线，用另一个带隙的环状天线接收， 证实了麦克斯韦关于电磁波存在的预言，这一重要的实验导致了后来无线电报的发明。从此 开始了电磁场理论应用与发展时代，并且发展成为当代最引人注目的学科之一。 无线电报 1895 年，意大利马可尼成功地进行了 2.5 公里距离的无线电报传送实验。1896 年，波 波夫进行了约 250 米距离的类似试验, 1899 年, 无 线电报跨越英吉利海峡的试验成功；1901 年，跨 越大西洋的 3200 公里距 离的试验成功。马可尼以 其在无线电报等领域的成就，获得了 1909 年的诺 贝尔奖金物 理学奖。无线电报的发明，开始了利 用电磁波时期。 有线电话 1876 年,美国 A.G.贝尔在美国建国 100 周年博览会上展示了他所发明 的有线电话。 此后,有线电话便迅速普及开来。 雷达（Radio Detection and Ranging） 二次世界大战前夕，飞机成为主要进攻武器。英、美、德、法等国竞相研制一类能够早期警 戒飞机的装置。1936 年，英国的瓦特设计的警戒雷达最先投入了运行。有效地警戒了来自德 国的轰炸机。1938 年，美国研制成第一部能指挥火炮射击的火炮控制雷达。1940 年，多腔磁 控管的发明，微波雷达的研制成为可能。1944 年，能够自动跟踪飞机的雷达研制成功。1945 年，能消除背景干扰显示运动目标的显示技术的发明,使雷达更加完善。在整个第二次世界大 战期间,雷达成了电磁场理论最活跃的部分。卫星通信技术 1958 年, 美国发射低轨的“斯科 尔”卫星成功,这是第一颗用于通信的试验卫星。1964 年,借助定点同步通信卫星首次实现了 美、 欧、非三大洲的通信和电视转播。1965 年,第一颗商用定点同步卫星投入运行。1969 年, 大西洋、太平洋和印度洋上空均已有定点同步通信卫星,卫星地球站已遍布世界各国，这些卫 星地球站又和本国或本地区的通信网接通。卫星通信经历 10 年的发展，终趋于成熟。 卫星定位技术 1957 年卫星发射成功后，人们试 图将雷达引入卫星，实现以卫星为基地 对地球表 面及近地空间目标的定位和导航。1958 年底，美 国开始研究实施这一计划， 于 1964 年研究成功子 午仪卫星导航系统。1973 年美国提出了由 24 颗卫星组成的实用系 统新方案，即 GPS 计划。它是英文 Navigation Satellite Timing and Ranging /Global Positioning System 的字头缩写 NAVSTAR/GPS 的简称，其含义是利用导航卫星 进 行测时和测距。1990 年最终的 GPS 方案是由 21 颗工作卫星和 3 颗在轨备用卫星组成。 三.三大类应用问题：

、电磁场（或电磁波）作为能量的一种形式，是 当今世界最重要的能源，其研究领 域涉及电磁 能量的产生、储存、变换、传输和综合利用。 、电磁波作为信息传输的载体，成为当今人类社会发布和获取信息的主要手段，主要 研究领域为信息的产生、获取、交换、传输、储存、处理、再现和综合利用。 电磁波作为探测未知世界的一种重要手段，主 要研究领域为电磁波与目标的相互 作用特性、 目际特征的获权与重建、探刘新技术等。 本意内容 1.1 矢量代数 1.2 三种常用的正交曲线坐标系 1.3 标量场的梯度 1.4 矢量场的通量与散度 1.5 矢量场的环流与旋度 1.6 无旅场与无散场 1.7 拉普拉斯运算与格林定理 1.8 亥姆霍兹定理 1.1矢量代数 1标最和矢量 标量：一个只用大小描述的物理量。 矢量：一个既有大小又有方向特性的物理量，常用黑体字 母或带箭头的字母表示。 失量的几何表示：一个失量可用一条有方向的线段来表示 矢量的代数表示： A=6A=EA A」 矢量的大小或模，A=同 矢量的几何表示 失量的单位失量： 常矢量：大小和方向均不变的矢量。 注意：单位失量不一定是常矢量。 矢量用坐标分量表示 A=&,A,+&,A,+e.A. A,Acosa A,=Acos B A.=Acosy

♥ 电磁场（或电磁波）作为能量的一种形式，是 当今世界最重要的能源，其研究领 域涉及电磁 能量的产生、储存、变换、传输和综合利用。 ♥ 电磁波作为信息传输的载体，成为当今人类社 会发布和获取信息的主要手段，主要 研究领域为信息的产生、获取、交换、传输、储存、处理、再现和综合利用。 ♥ 电磁波作为探测未知世界的一种重要手段，主 要研究领域为电磁波与目标的相互 作用特性、 目标特征的获取与重建、探测新技术等。 本章内容 1.1 矢量代数 1.2 三种常用的正交曲线坐标系 1.3 标量场的梯度 1.4 矢量场的通量与散度 1.5 矢量场的环流与旋度 1.6 无旋场与无散场 1.7 拉普拉斯运算与格林定理 1.8 亥姆霍兹定理 1.1 矢量代数 1. 标量和矢量 标量：一个只用大小描述的物理量。 矢量：一个既有大小又有方向特性的物理量，常用黑体字 母或带箭头的字母表示。 矢量的几何表示：一个矢量可用一条有方向的线段来表示 矢量的代数表示： A eA A eA A     = = 矢量的大小或模： A A  = 矢量的单位矢量： A A eA   = 常矢量：大小和方向均不变的矢量。 注意：单位矢量不一定是常矢量。 矢量用坐标分量表示 x x y y z Az A e A e A e     = + +    cos cos cos A A A A A A z y x = = = A  矢量的几何表示 z Ax  A Ay A z x y    O

A=A(e,cosa+cosB+.cosy) e=e,cosa+e,cosB+e.cosy 2.矢量的代数运算 (1)矢量的加减法 两矢量的加减在几何上是以这两矢量为邻边的平行四边形的对角线，如图所示。 在直角坐标系中两矢量的加法和减法： A±B=e,(A,±B,)+e,(A±B,)+e.(A±B) 矢量的加减符合交换律和结合律 交换律：A+B=B+A 交换律：A+(B+C=(a+E)+C (2)标量乘失量 kA=e kA,+ekA,+e.kA. (3)矢量的标积（点积) A.B=AB COS0=A,B,+A,B,+A.B. AB=B·A一一矢量的标积符合交换律 A1B→A.B=0 AIB→A.B=AB e,e,=e,e.=e.=0 e·e=e,·e,=e.e.=1 (4)矢量的失积（叉积） A×B=eABsin0 用坐标分量表示为.xB=E,(4B-AB,)+元，(AB-AB,)+E(LB 写成行列式形式为： A× ee e. A×B=AA,A B B.B,B. AB sin q A AxB=-BxA 矢量A与B的叉积

( cos cos  cos  ) x y z A A e e e     = + + cos cos  cos A x y z e e e e     = + + 2. 矢量的代数运算 （1）矢量的加减法 两矢量的加减在几何上是以这两矢量为邻边的平行四边形的对角线,如图所示。 在直角坐标系中两矢量的加法和减法： ( ) ( ) ( ) x x x y y y z Az Bz A B = e A  B + e A  B + e       矢量的加减符合交换律和结合律 交换律： A B B A     + = + 交换律： A B C A B C       + ( + ) = ( + ) + （2）标量乘矢量 x x y y z z kA e kA e kA e kA     = + + （3）矢量的标积（点积） A B = AB = AxBx + AyBy + AzBz  cos   A B B A      =  ——矢量的标积符合交换律 A B   ⊥ A B = 0   A B   // AB = AB   ex ey = ey ez = ez ex = 0       ex ex = ey ey = ez ez =1       （4）矢量的矢积（叉积） A B enABsin      = 用坐标分量表示为: A B ex (AyBz AzBy ) ey (AzBx AxBz ) ez (AxB       = − + − + 写成行列式形式为: x y z x y z x y z B B B A A A e e e A B       = A B B A      = −  q AB sin q A B    B  A  矢量 A 与 B 的叉积

若A⊥B则A×B=AB 若A〃B则Ax武=0 (5)矢量的混合运算 (4+B)-C=4.C+B.C 一一分配律 (4+B)xC=4xC+BxC 一分配律 A:(BxC=B(C×小=C-(dxB)一一标量三重积 Ax(B×C⊙)=(A.CB-(A.BG 一一矢量三重积 1.2三种常用的正交曲线坐标系 三维空间任意一点的位置可通过三条相互正交曲线的交点来确定。 三条正交曲线组成的确定三维空间任意点位置的体系，称为正交曲线坐标系；三条正交 曲线称为坐标轴；描述坐标轴的量称为坐标变量。 在电磁场与波理论中，三种常用的正交曲线坐标系为：直角坐标系、圆柱坐标系和球坐 标系。 1.直角坐标系 平面) dz 点Px0,y0,z0) dy ds. y=y0(平面) =0(平面》 直角坐标系 直角坐标系的长度元、面积元、体积元 坐标变量： x.y, 坐标单位矢量： exese: 位置矢量： r=ex+ey+ez 线元矢量： di=e,dr+e,dy+e.d止 面元矢量 dS,=e,dl dl.=edyd= dS,-e,dld山.-e,drd

若 A B   ⊥ 则 AB = AB   若 A B   // 则 A B = 0   （5）矢量的混合运算 A B C A C B C        ( + ) =  +  —— 分配律 A B C A C B C        ( + ) =  +  —— 分配律 A (B C) B (C A) C (A B)            =   =   —— 标量三重积 A B C A C B A B C          (  ) = (  ) − (  ) —— 矢量三重积 1.2 三种常用的正交曲线坐标系 三维空间任意一点的位置可通过三条相互正交曲线的交点来确定。 三条正交曲线组成的确定三维空间任意点位置的体系，称为正交曲线坐标系；三条正交 曲线称为坐标轴；描述坐标轴的量称为坐标变量。 在电磁场与波理论中，三种常用的正交曲线坐标系为：直角坐标系、圆柱坐标系和球坐 标系。 1. 直角坐标系 坐标变量： x, y,z 坐标单位矢量： x y z e e e    , , 位置矢量 ： r e x e y e z x y z     = + + 线元矢量： l e x e y e z d xd yd zd     = + + 面元矢量； S e l l e y z d x xd yd z xd d    = = S e l l e x z d y yd xd z yd d    = = 点P(x0,y0,z0) 0 y = y （平面） o x y z 0 x = x （平面） 0 z = z （平面） P 直角坐标系 ex  ez  ey  x y z 直角坐标系的长度元、面积元、体积元 o dz d y dx S e y z d x xd d   = dSz ezdxdy   = S e x z d y yd d   =

dS.=e.dl,dl,=e.dxdy 体积元： dV=dxdyd= 2.圆柱坐标系 =8,(圆面 二=0（平面） 球山 P(ro.Bo.do) P=Po (圆柱面) 中=4 一（半平面 (半平面) 球坐标系 圆柱坐标 坐标变量 坐标单位矢量 epese: 位置矢量 F=ep+e= 线元失量 di-edp+epdo+e.d正 d5。=edl,dl.=e.pdd d。=e,dldl.=e,dpd 面元矢量 ds.=e.dldl。=e.pdpd 体积元 dV=pdpdd 3.球坐标系 d -de

S e l l e x y d z zd xd y zd d    = = 体积元 ： dV = dxdydz 2. 圆柱坐标系 坐标变量 ,,z 坐标单位矢量 z e e e    , ,   位置矢量 r e e zz    =  + 线元矢量 l e e e z d d d zd     =   +   + 面元矢量               = = = = = =                 d d d d d d d d d d d d d d d z z z z z S e l l e S e l l e z S e l l e z          体积元 dV = dddz 3. 球坐标系 圆柱坐标 系  =0 （半平面）  = 0 （圆柱面） z = z0 （平面） ( , , ) 0 0 0 P   z 圆柱坐标系中的线元、面元和体积元 球坐标系 球坐标系中的线元、面元和体积元

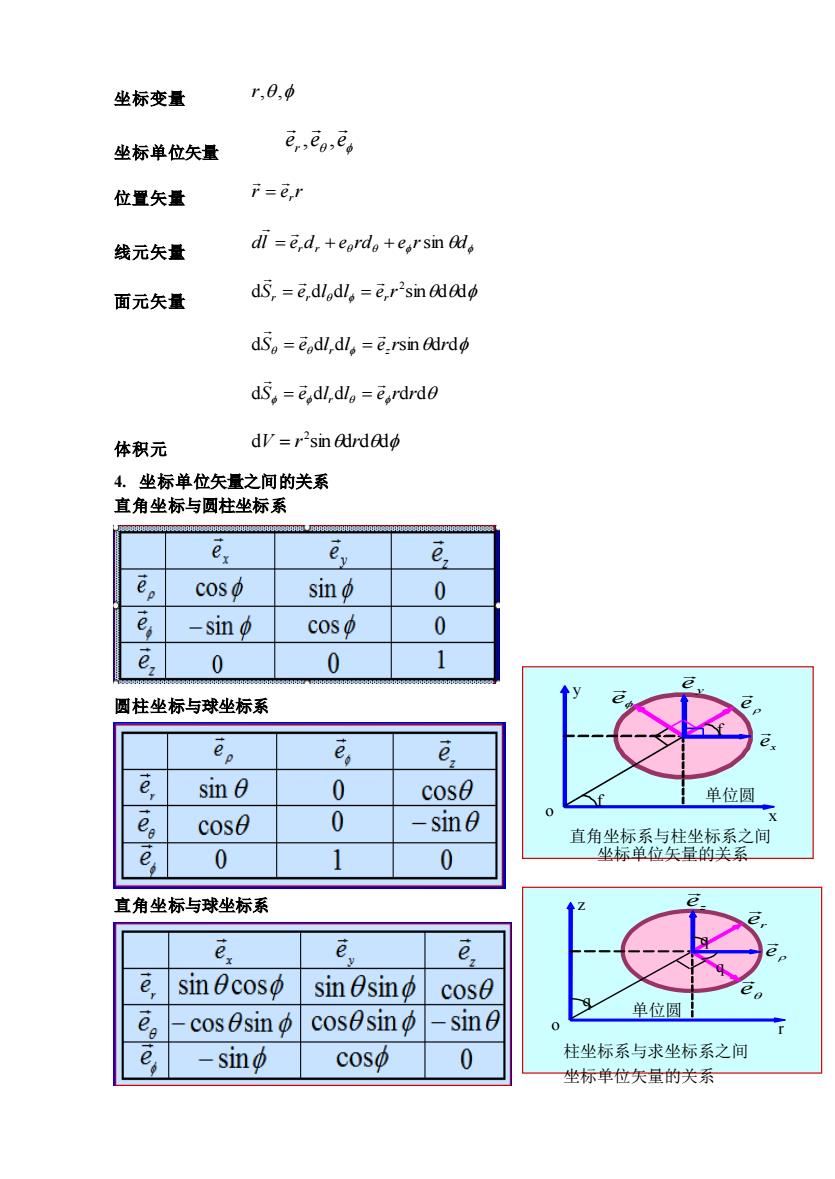
坐标变量 r.0.0 坐标单位矢量 e,eoses 位置失量 F=er 线元矢量 dl =ed,+eordo+ersin ad, 面元矢量 dS,=e,dld山，=e,r2sin69 dS。=ed,d。=e.rsin dS。=e,dl,d。-e,rdrd0 体积元 dy=r"sin ardao 4.坐标单位矢量之间的关系 直角坐标与圆柱坐标系 e e g cos sin 0 e -sin coso 0 e: 0 0 圆柱坐标与球坐标系 e sin 0 0 cose 单位圆 cos0 0 -sin e, 0 1 0 直角坐标与球坐标系 e.sin0coso sinθsin cose 单位圆} e。 cosesin cosesin-sine -sino coso 0 柱坐标系与求坐标系之间 坐标单位关量的关系

坐标变量 r,, 坐标单位矢量   e e e r    , , 位置矢量 r e rr   = 线元矢量    d dl e d e rd e r r r = + + sin   面元矢量 d d d  sindd 2 S e l l e r r r r    = = dS edl rdl  ez rsindrd    = = dS edl rdl  e rdrd    = = 体积元 d sind dd 2 V = r r 4. 坐标单位矢量之间的关系 直角坐标与圆柱坐标系 圆柱坐标与球坐标系 直角坐标与球坐标系 o f x y 单位圆 直角坐标系与柱坐标系之间 坐标单位矢量的关系 f e x  e y  e   e  o q r z 单位圆 柱坐标系与求坐标系之间 坐标单位矢量的关系 q q e z  e   e r  e 

1.3标量场的梯度 标量场和矢量场 确定空间区域上的每一点都有确定物理量与之对应，称在该区域上定义了一个场。 如果物理量是标量，称该场为标量场。 例如：温度场、电位场、高度场等。 如果物理量是矢量，称该场为矢量场。 例如：流速场、重力场、电场、磁场等」 如果场与时间无关，称为静态场，反之为时变场。 从数学上看，场是定义在空间区域上的函数： 标量场的等值线（面） 静态标量场和矢量场可分别表示为：(x,八，2人F(x,八，) 时变标量场和矢量场可分别表示为：x,y,二，)、F(x,y,2,) 1.标量场的等值面 等值面：标量场取得同一数值的点在空间形成的曲面。 意义：形象直观地描述了物理量在空间的分布状态。 等值面方程：x,水)=C 等值面族 等值面的特点： (1)常数C取一系列不同的值，就得到一系列不同的等值面，形成等值面族： (2)标量场的等值面充满场所在的整个空间； (3)标量场的等值面互不相交。 2.方向导数 .w-密caa+s是wr 式中cosL,cosB,cosy-一△/的方向余弦。 意义：方向导数表示场沿某方向的空间变化率。 -一uM沿I方向增加： S:Ou 0一-一沿1方向减少： Ou S: 可0 一u0沿7方向无变化： 特点：方向导数既与点M0有关，也与方向有关。 问题：在什么方向上变化率最大、其最大的变化率为多少？ 3.标量场的梯度8 radu或Vu

1.3 标量场的梯度 标量场和矢量场 确定空间区域上的每一点都有确定物理量与之对应，称在该区域上定义了一个场。 如果物理量是标量，称该场为标量场。 例如：温度场、电位场、高度场等。 如果物理量是矢量，称该场为矢量场。 例如：流速场、重力场、电场、磁场等。 如果场与时间无关，称为静态场，反之为时变场。 从数学上看，场是定义在空间区域上的函数： 静态标量场和矢量场可分别表示为： u(x, y,z)、F(x, y,z)  时变标量场和矢量场可分别表示为： u(x, y,z,t)、F(x, y,z,t)  1.标量场的等值面 等值面: 标量场取得同一数值的点在空间形成的曲面。 意义: 形象直观地描述了物理量在空间的分布状态。 等值面方程： u(x, y,z) = C 等值面的特点： （1）常数 C 取一系列不同的值，就得到一系列不同的等值面，形成等值面族； （2）标量场的等值面充满场所在的整个空间； （3）标量场的等值面互不相交。 2. 方向导数 概念： | lim cos cos  cos 0 0 z u y u x u l u l u l M   +   +   =   =    → 式中 cos,cos ,cos —— l   的方向余弦。 意义：方向导数表示场沿某方向的空间变化率。 §：  0   l u ——u(M)沿 l  方向增加； §：  0   l u ——u(M)沿 l  方向减少； §： = 0   l u ——u(M)沿 l  方向无变化； 特点：方向导数既与点 M0 有关，也与方向有关。 问题：在什么方向上变化率最大、其最大的变化率为多少？ 3. 标量场的梯度 gradu或u 标量场的等值线(面) 等值面族 u=c2 u=c3 u=c1 M0 l M Δl 方向导数的概念

概念： m=一，其中-一司，取得最大值的方向， 意义：描述标量场在某点的最大变化率及其变化最大的方向 梯度的表达式： 直角坐标系 圆柱坐标系 ap 1 ou 球坐标系 梯度的性质： 1标量场的梯度是矢量场，它在空间某点的方向表示该点场变化最大（增大）的方向，其数 值表示变化最大方向上场的空间变化率。 2标量场在某个方向上的方向导数，是梯度在该方向上的投影。 3标量场的梯度垂直于通过该点的等值面（或切平面） 梯度运算的基本公式： 7C=0 V(Cu)=CVu V(u±v)=Vu±Vy V(uv)=uVv+vVu Vf(u)=f(u)u 例12.1设一标量函数（x,八2)=r+少-2描述了空间标量场。试求： (山)该函数P在点P(1,1,)处的梯度，以及表示该梯度方向的单位矢量。 ②求该函数P沿单位矢量9=8，c0s60°+日，0s45+已.c0s60方向的方向 导数，并以点P(1,1,1)处的方向导数值与该点的梯度值作以比较，得出相应结论。 解()由梯度计算公式，可求得P点的梯度为 =(e,2x+e,2y-e.)d=e,2+e,2-e. 表征其方向的单位矢量

概念： max | l u u el    =  ，其中 l u el   − −  ，取得最大值的方向。 意义：描述标量场在某点的最大变化率及其变化最大的方向 梯度的表达式： 直角坐标系 z u e y u e x u u ex y z   +   +    =    圆柱坐标系 z u e u e u u e z   +   +    =         1 球坐标系        +   +    = u r e u r e r u u er sin   1  1 梯度的性质： 1 标量场的梯度是矢量场，它在空间某点的方向表示该点场变化最大（增大）的方向，其数 值表示变化最大方向上场的空间变化率。 2 标量场在某个方向上的方向导数，是梯度在该方向上的投影。 3 标量场的梯度垂直于通过该点的等值面（或切平面） 梯度运算的基本公式：           =    =  +    =     =   = f u f u u uv u v v u u v u v Cu C u C ( ) ( ) ( ) ( ) ( ) 0 例 1.2.1 设一标量函数 x y z = x + y − z 2 2 （ , , ） 描述了空间标量场。试求： (1) 该函数  在点 P(1,1,1) 处的梯度，以及表示该梯度方向的单位矢量。 (2) 求该函数  沿单位矢量 o o o el ex cos60 ey cos 45 ez cos60     = + + 方向的方向 导数，并以点 P(1,1,1) 处的方向导数值与该点的梯度值作以比较，得出相应结论。 解 (1)由梯度计算公式，可求得 P 点的梯度为 P x y z P x y z z e y e x [(e )( )] 2 2 + −   +   +    =     x y z x y z e x e y e e e e       = ( 2 + 2 − ) (1,1,1) = 2 + 2 − 表征其方向的单位矢量

8同-nbw6号5号-e时 70 e2x+e2y-e. (2)由方向导数与梯度之间的关系式可知，沿！方向的方向导数为 -p减=62+62-605号 al +-月 对于给定的P点，上述方向导数在该点取值为 4 2w=1+25 7 而该点的梯度值为 0。=V2x)2+(2y)2+(-1)2lw=3 显然，梯度P叫描述了P点处标量函数？的最大变化率，即最大的方向导数，故 含4 恒成立。 1.4矢量场的通量与散度 1.矢量线 概念：矢量线是这样的曲线，其上每一点的切线方向代表了该点矢量场的方向： 意义：形象直观地描述了矢量场的空间分布状态。 矢量线方程： d dy d Fx,y,FK,y,Fx,y,可 2.矢量场的通量 问题：如何定量描述矢量场的大小？ 引入通量的概念。 通量的概念 w=「dw-「Fds-[F.e,dS 其中：否=5_一面积元矢量 已，一一面积元的法向单位矢量： dy=Fe ds 一穿过面积元S的通量

3 1 3 2 3 2 | (2 ) (2 ) ( 1) 2 2 | 1,1,1 2 2 2 x y z x y z l p e e e x y e x e y e e        = + − + + − + − =   = （ ）   (2) 由方向导数与梯度之间的关系式可知，沿 el 方向的方向导数为 ) 2 1 2 2 2 1 ( 2 2 ) ( l x y z x y z e e x e y e e e e l        =   = + −  + +     2 1 = x + 2y − 对于给定的 P 点，上述方向导数在该点取值为 2 1 2 2 | 2 1 | 2 (1,1,1) + = + − =   x y l u p 而该点的梯度值为 (2 ) (2 ) ( 1) | (1,1,1) 3 2 2 2  = x + y + − = P  显然，梯度 P  描述了 P 点处标量函数  的最大变化率，即最大的方向导数，故 P P l       | 恒成立。 1.4 矢量场的通量与散度 1. 矢量线 概念：矢量线是这样的曲线，其上每一 点的切线方向代表了该点矢量场的方向。 意义：形象直观地描述了矢量场的空间分布状态。 矢量线方程： ( , , ) d ( , , ) d ( , , ) d F x y z z F x y z y F x y z x x y z = = 2. 矢量场的通量 问题：如何定量描述矢量场的大小？ 引入通量的概念。 通量的概念 d F dS F endS s s     . .     =  = = 其中: dS endS   = ——面积元矢量； n e  ——面积元的法向单位矢量； d F endS    = . ———穿过面积元 dS  的通量。 矢量线 O M F r r r + d dr