
近代物理实验》 二维流体流动的格子玻耳兹曼模拟 房文静 近代物理实验》 中因石油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 《近代物理实验》 房文静 二维流体流动的格子玻耳兹曼模拟

二维流体流动的格子玻耳滋曼模拟 格子玻耳兹曼方法简介 离散速度模型 实验6-3二维流体流动的格子玻耳兹曼模拟 《近代物理实验》 中圆石油大学 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 二维流体流动的格子玻耳兹曼模拟 n 格子玻耳兹曼方法简介 n 离散速度模型 n 实验6-3 二维流体流动的格子玻耳兹曼模拟

格子玻耳兹曼方法简介 格子玻耳兹曼方法(Lattice Boltzmann Method,LBM)是用简 单的微观模型来模拟流体宏观行为的一种新方法。优点: (1)算法简单; (2)能够处理复杂的边界条件; (3)格子玻尔兹曼方法中的压力可由状态方程直接求解; (4)编程容易,计算的前后处理也非常简单; (5)具有很高的并行性: (6)能直接模拟有复杂几何边界的诸如多孔介质等连通域流场,无 须作计算网格的转换。 近代物理实验》 中因方油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 格子玻耳兹曼方法简介 格子玻耳兹曼方法(Lattice Boltzmann Method,LBM)是用简 单的微观模型来模拟流体宏观行为的一种新方法。优点: (1)算法简单; (2)能够处理复杂的边界条件; (3)格子玻尔兹曼方法中的压力可由状态方程直接求解; (4)编程容易,计算的前后处理也非常简单; (5)具有很高的并行性; (6)能直接模拟有复杂几何边界的诸如多孔介质等连通域流场,无 须作计算网格的转换

格子玻耳兹曼方法简介 思路:将流体及其存在的时间和空间完全离散,给出离散的流体 分子之间相互作用以及迁移的规则。流体分子存在于空间网格上,用 速度分布函数来描述某时刻,位于某空间处的节点的分子数。分子在 每一个时间步长的演化包括两部分:(a)迁移,分子沿速度方向向距离 最近的节点运动:(b)碰撞,当不同的分子同时到达某个节点时,按照一 定的碰撞规则发生碰撞并改变运动方向。这样经过较长时间可以获得 流体的宏观特性。 《近代物理实验》 中因不油大学闲 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 格子玻耳兹曼方法简介 思路:将流体及其存在的时间和空间完全离散,给出离散的流体 分子之间相互作用以及迁移的规则。流体分子存在于空间网格上,用 速度分布函数来描述某时刻,位于某空间处的节点的分子数。分子在 每一个时间步长的演化包括两部分:(a)迁移,分子沿速度方向向距离 最近的节点运动;(b)碰撞,当不同的分子同时到达某个节点时,按照一 定的碰撞规则发生碰撞并改变运动方向。这样经过较长时间可以获得 流体的宏观特性

格子玻耳兹曼方法简介 三个重要假设: (1)分子互相碰撞时只考虑二体碰撞,即认为3个分子或者3 个以上分子同时碰撞在一起的几率很小: (2)分子混沌假设,这一假设认为各个分子的速度分布是不 依赖于另外的分子而独立的,即粒子在碰撞之前速度不相关: (3)外力不影响局部碰撞的动力学行为。 近代物理实验》 中因石油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 格子玻耳兹曼方法简介 三个重要假设: (1)分子互相碰撞时只考虑二体碰撞,即认为3个分子或者3 个以上分子同时碰撞在一起的几率很小; (2)分子混沌假设,这一假设认为各个分子的速度分布是不 依赖于另外的分子而独立的,即粒子在碰撞之前速度不相关; (3)外力不影响局部碰撞的动力学行为

格子玻耳兹曼方法简介 简化的Boltzmann方程为: of ∂f ∂f ∂t a BE u(fea-fy 离散的Boltzmann方程为 Ja(r+ea0t,t+ot)-fa(r,t)=-fa(r,t)-fea(r,t)]+o:Fa(r,t) 完整的格子Boltzmann模型组成:格子(离散速度模型)、平衡态 分布函数、分布函数的演化方程。 K 《近代物理实验》 中阁石油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 格子玻耳兹曼方法简介 简化的Boltzmann方程为: 离散的Boltzmann方程为 完整的格子Boltzmann模型组成:格子(离散速度模型)、平衡态 分布函数、分布函数的演化方程

离散速度模型 常用的离散速度模型有二维的D2Q9模型 不含外力时的Boltzmann方程为 fa(r+ea0t,t+0t)-fa(r,t)=-fa(r,t)-fo(r,t)] 速度空间矢量为 (0,0) a=0 ea c(cos[(a-1)引,sin(a-1)1) a=1,2,3,4 V2c(cos[(2a-1)别,sin[(2a-1)]) a=5,6,7,8 近代物理实验》 中因石油大学雨 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 离散速度模型 常用的离散速度模型有二维的D2Q9模型 不含外力时的Boltzmann方程为 速度空间矢量为
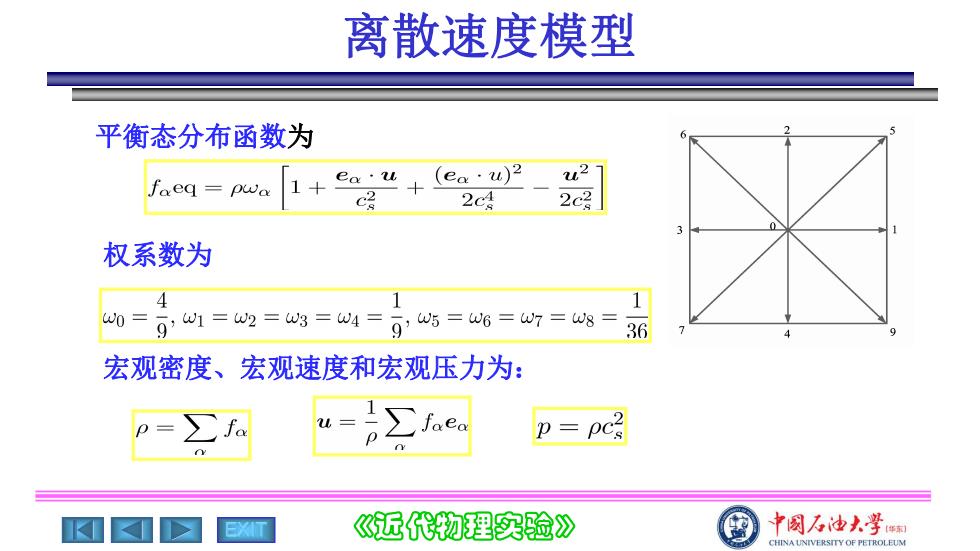
离散速度模型 平衡态分布函数为 ea·u (ea·u)2 22 faeq=pwa c 2c4 2c 权系数为 1 w0= g1=2=w3=w4= w5=W6=w7=W8= 36 宏观密度、宏观速度和宏观压力为: p=∑fa faea p=pc 《近代物理实验》 中阁石油大孝闲 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 离散速度模型 权系数为 平衡态分布函数为 宏观密度、宏观速度和宏观压力为:

二维流体流动的格子玻耳兹曼模拟 二维流体流动的格子玻耳兹曼模拟实验的基本目的: (1)了解格子玻耳兹曼方法的基本思想。 (2)学会格子玻耳兹曼方法的几种常用格子划分和边界条件处理 方法。 (3)掌握格子玻耳兹曼方法模拟简单边界条件流体流动的方法。 (4)掌握格子玻耳兹曼方法模拟结果的可视化方法。 近代物理实验》 中因石油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 Ø 二维流体流动的格子玻耳兹曼模拟实验的基本目的: (1)了解格子玻耳兹曼方法的基本思想。 (2)学会格子玻耳兹曼方法的几种常用格子划分和边界条件处理 方法。 (3)掌握格子玻耳兹曼方法模拟简单边界条件流体流动的方法。 (4)掌握格子玻耳兹曼方法模拟结果的可视化方法。 二维流体流动的格子玻耳兹曼模拟

实验6-3二维流体流动的格子玻耳兹曼模拟 1、基础性实验内容 (1)顶盖驱动流的LBM模拟 基本特征是:流动稳定后,方腔 的中央一个一级大涡出现,而在左下 角和右下角分别出现一个二级涡,当 雷诺数R©超过一临界值后,在方腔的 左上角还会出现一个涡。 《近代物理实验》 中阁石油大学脚 CHINA UNIVERSITY OF PETROLEUM
EXIT 《近代物理实验》 实验6-3二维流体流动的格子玻耳兹曼模拟 1、基础性实验内容 (1)顶盖驱动流的LBM模拟 基本特征是:流动稳定后,方腔 的中央一个一级大涡出现,而在左下 角和右下角分别出现一个二级涡,当 雷诺数Re超过一临界值后,在方腔的 左上角还会出现一个涡