第5章均匀平面波在无界空间中的传播(内容不用多修改了,不然格式会变化) 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波 均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。 本章内容 5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速 5.5均匀平面波在各向异性媒质中的传播 5.1理想介质中的均匀平面波 5.1.1 一维波动方程的均匀平面波解 5.1.2理想介质中均匀平面波的传播特点 5.1.3沿任意方向传播的均匀平面波 5.1,1一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想介质。均匀平面波沿z轴传播, 则电场强度和磁场强度均不是x和y的函数,即 aE aE o,00-0→E=0,n=0 A-2 由于 6蓝装+-0→-0→6=0 月-设00-0>=n +2E.=0 同理 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播方向一 横电磁波(TEM波) 设电场只有x分量,即 d'E,@+kE,(e)=0 E(e)=e,E,(e)→d正 其解为: E,(=)=Ae+e
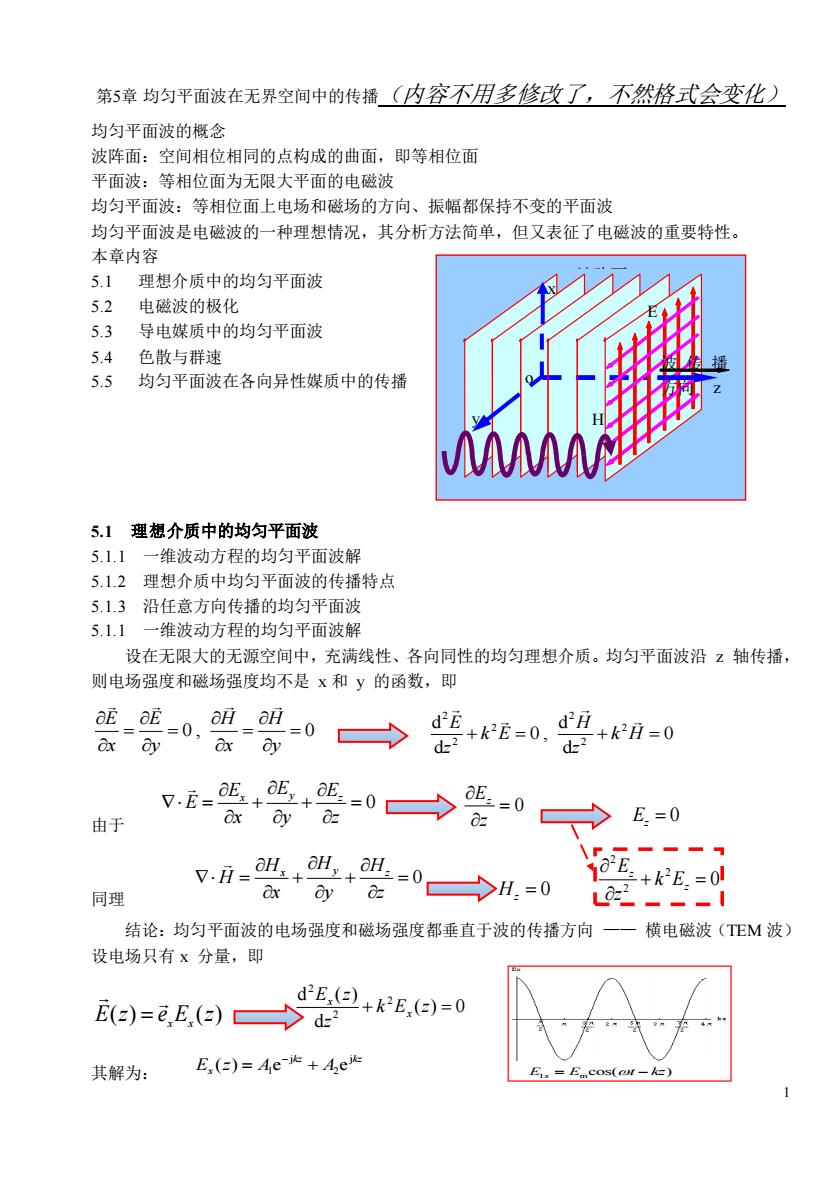
1 第5章 均匀平面波在无界空间中的传播(内容不用多修改了,不然格式会变化) 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波 均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。 本章内容 5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速 5.5 均匀平面波在各向异性媒质中的传播 5.1 理想介质中的均匀平面波 5.1.1 一维波动方程的均匀平面波解 5.1.2 理想介质中均匀平面波的传播特点 5.1.3 沿任意方向传播的均匀平面波 5.1.1 一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想介质。均匀平面波沿 z 轴传播, 则电场强度和磁场强度均不是 x 和 y 的函数,即 0 , 0 E E H H x y x y = = = = 2 2 2 2 2 2 d d 0 , 0 d d E H k E k H z z + = + = 由于 0 x y z E E E E x y z = + + = 0 E z z = 0 E z = 同理 0 x y z H H H H x y z = + + = 0 H z = 2 2 2 0 z z E k E z + = 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播方向 —— 横电磁波(TEM 波) 设电场只有 x 分量,即 E(z) e E (z) x x = ( ) 0 d d ( ) 2 2 2 + k E z = z E z x x k = 其解为: j j 1 2 ( ) e e kz kz E z A A x − = + E H z 波传播 方向 波阵面 x y o 的波形 1 mcos( ) E E t kz x = −
解的物理意义 第一项 E(=)=Aeik=Eeleik E(=,t)=Re[Eeiue ieic ]Em cos(ot-k+) 可见,4e表示沿±:方向传播的波。 第二项 E.e)=4c=Ecc←、 E(,1)=Re[Emeieei ]=Em cos(+) 沿一z方向传播 相伴的磁场 由7×E=-j@H,可得 磁场与电场相互 垂直,且同相位 e.xE ou dz E) 其中 称为媒质的本征阻拉。在真空中 凸=120x=3779 n=- 同理,对于 E2=eE,=e heik 结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂直,且同相位 5.1.2理想介质中均匀平面波的传播特点 1.均匀平面波的传播参数 (1)角频率、频率和周期 角频率。:表示单位时间内的相位变化,单位为rad/s 周期T:时间相位变化2π的时间间隔,即 OT-2 ( 频率f: (2)波长和相位常数 波长入:空间相位差为2丌的两个波阵面的间距,即 E(0.1)=Ecosor
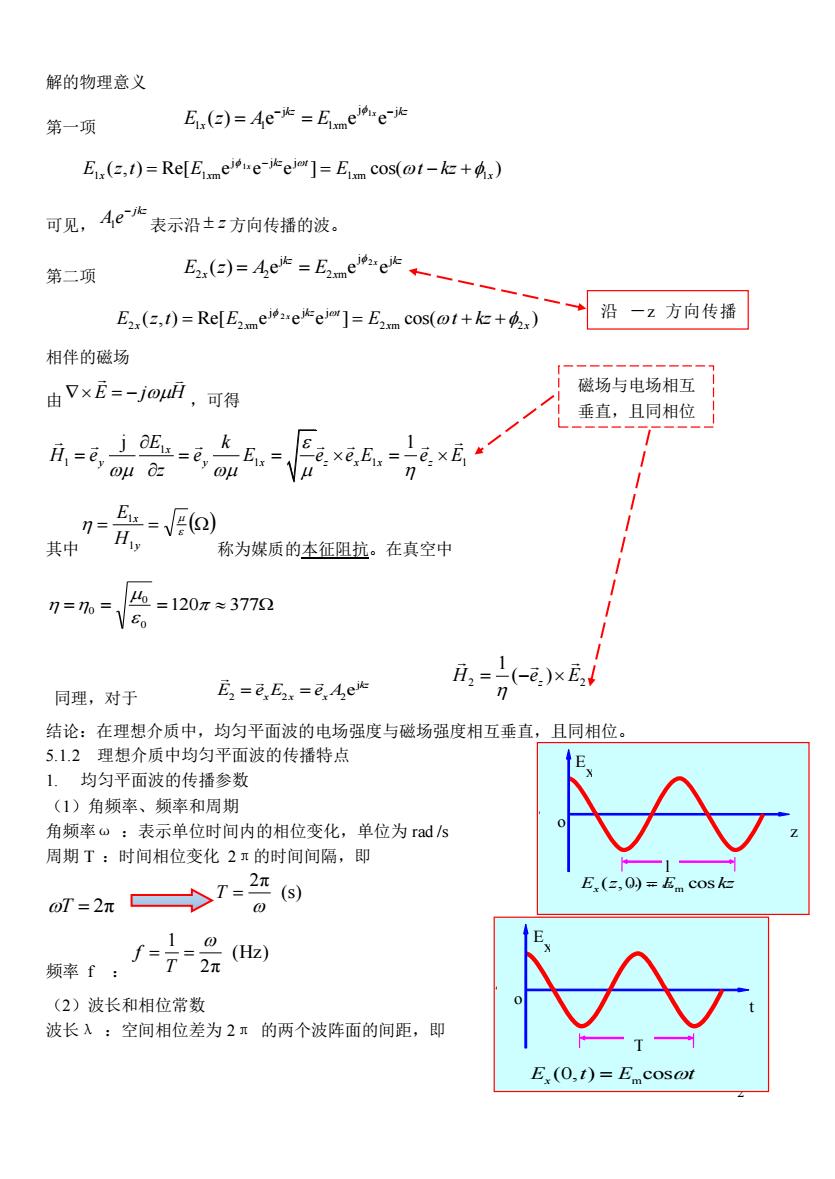
2 解的物理意义 第一项 1 j j j 1 1 1 m ( ) e e e kz kz x E z A E x x − − = = 1 j j j 1 1 m 1 m 1 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x − = = − + 可见, jkz Ae − 1 表示沿 z 方向传播的波。 第二项 2 j j j 2 2 2 m ( ) e e e kz kz x E z A E x x = = 2 j j j 2 2 m 2 m 2 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x = = + + 相伴的磁场 由 E j H = − ,可得 1 1 1 1 1 j 1 x y y x z x x z E k H e e E e e E e E z = = = = 其中 = = () y x H E 1 1 称为媒质的本征阻抗。在真空中 = = =120 377 0 0 0 同理,对于 j 2 2 2e kz E e E e A = = x x x 2 2 ( ) 1 H ez E = − 结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂直,且同相位。 5.1.2 理想介质中均匀平面波的传播特点 1. 均匀平面波的传播参数 (1)角频率、频率和周期 角频率ω :表示单位时间内的相位变化,单位为 rad /s 周期 T :时间相位变化 2π的时间间隔,即 T = 2π 2π T (s) = 频率 f : 1 (Hz) 2π f T = = (2)波长和相位常数 波长λ :空间相位差为 2π 的两个波阵面的间距,即 沿 -z 方向传播 的波 磁场与电场相互 垂直,且同相位 t T o x E E t E t x (0, ) cos = m o x E l z E z E kz x ( ,0) cos 的曲线 = m

a:a女-祭-应m 1 相位常数k:表示波传播单位距离的相位变化 k=2(adm) k的大小等于空间相位2π内所包含的波长数目,因此也称为波数 (3)相速(波速) 相速:电磁波的等相位面在空间中的移动速度 由o-k=C>o-k他=0 故得到均匀平面波的相速为 1m/9)←- 相速只与媒质参数有关,而 与电磁波的频率无关 1 1 v=C=- =3×103(m/s) 480 真空中: x10×3610 2、能量密度与能流密度 由于 =×E 电场能量与磁场能量相同 ,于是有 "=5s=3川=w一 故 p=w。+wn=e武=l 理想介质中均有 5=xie0=ecasio-k+A) 面波的和 wRe()x -总8 ="-→ 能量的传输速度等于相速 3、理想介质中的均匀平面波的传播特点(P196页) 根据前面的分析,可总结出理想介质中的均匀平面波的传播特点为: (1)电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)。 (2)无衰减,电场与磁场的振幅不变。 (3)波阻抗为实数,电场与磁场同相位。 (4)电磁波的相速与频率无关,无色散。 (⑤)电场能量密度等于磁场能量密度,能量的传输速度等于相速
3 k = 2π 2π 1 (m) k f = = 相位常数 k :表示波传播单位距离的相位变化 2π k (rad/m) = k 的大小等于空间相位 2π内所包含的波长数目,因此也称为波数。 (3)相速(波速) 相速 v:电磁波的等相位面在空间中的移动速度 由 t −kz =C d d 0 t k z − = 故得到均匀平面波的相速为 (m s) 1 d d = = = = t k z v 真空中: 8 0 0 7 9 1 1 3 10 (m/s) 1 4π 10 10 36π v c − − = = = = 2、能量密度与能流密度 由于 H ez E = 1 ,于是有 2 2 e m 1 1 2 2 w E H w = = = 故 2 2 w w w E H e m = + = = 2 2 m 1 ( , ) ( , ) cos ( ) 2 S E z t H z t e E t kz z x = = − + 2 2 av m m 1 1 2 2 w E H = = * 2 av m 1 1 Re[ ( ) ( )] 2 2 S E z H z e E z = = 2 m av 1 1 2 z e E w v = = 3、理想介质中的均匀平面波的传播特点(P196 页) 根据前面的分析,可总结出理想介质中的均匀平面波的传播特点为: (1)电场、磁场与传播方向之间相互垂直,是横电磁波(TEM 波)。 (2)无衰减,电场与磁场的振幅不变。 (3)波阻抗为实数,电场与磁场同相位。 (4)电磁波的相速与频率无关,无色散。 (5)电场能量密度等于磁场能量密度,能量的传输速度等于相速。 相速只与媒质参数有关,而 与电磁波的频率无关 电场能量与磁场能量相同 能量的传输速度等于相速 x y z E H O 理想介质中均匀平 面波的 和 E H

例5.1.1频率为9.4GH的均匀平面波在聚乙烯中传播,设其为无耗材料,相对介电常数为 £,=226。若磁场的振幅为7mm,求相速、波长、波阻抗和电场强度的幅值。 解:由题意 6,=2.26,f=9.4×10°Hz 因此 _1.996×10 =710 =2.12m 、377 n后左26210 Em=Hn=7×103×251=1.757V/m 例5.1.2 均匀平面波的感场强度的振相为行4 ,以相位常数为30radm在空气中沿一e方 向传插。当1=0和:=0时,若户取向为一已,试写出E和户的表示式,并求出频率和波长。 解:以余弦为基准,直接写出 i(e,0=-6,3元oso+B阳)ANm E(=,1)=nH(=,t)x(-e.)=e40cos(ot+Bz)V/m 因B=30rad/m,故 =音-新=021m,-号g-兰0=1450业 B30 则 月e,0=-6元co90x101+30a)Wm E(,=e,40cos(90×101+30z)Vm 例5.1.3频率为100Mz的均匀电磁波,在一无耗媒质中沿+: 该媒质的相对介电常数8,=4、相对磁导率4,=1,且当t一
4 例 5.1.1 频率为 9.4GHz 的均匀平面波在聚乙烯中传播,设其为无耗材料,相对介电常数为 r = 2.26 。若磁场的振幅为 7mA/m,求相速、波长、波阻抗和电场强度的幅值。 解:由题意 9 r = = 2.26 , 9.4 10 Hz f 因此 0 0 8 r 1.996 10 m/s 2.26 v v v = = = 8 9 1.996 10 2.12 m 9.4 10 v f = = = 0 r 377 251 2.26 = = = = 3 m m E H 7 10 251 1.757 V/m − = = = 例 5.1.2 均匀平面波的磁场强度的振幅为 A m 3 1 ,以相位常数为 30 rad/m 在空气中沿 z e − 方 向传播。当 t = 0 和 z = 0 时 ,若 H 取向为 y e − ,试写出 E 和 H 的表示式,并求出频率和波长。 解:以余弦为基准,直接写出 1 ( , ) cos( ) A/m 3π H z t e t z = − + y E(z,t) =0H(z,t)(−e z ) = e x 40cos(t + z) V/m 因 = 30rad m ,故 2π 2π 0.21 m , 30 === 8 3 10 45 8 9 10 1.43 10 Hz π /15 π c f = = = = 则 1 8 ( , ) cos(90 10 30 ) A/m 3π H z t e t z = − + y ( , ) 40cos(90 10 30 ) V/m 8 E z t e t z = x + 例 5.1.3 频率为 100Mz 的均匀电磁波,在一无耗媒质中沿 + z 方向传播,其电场 xEx E e = 。已知 该媒质的相对介电常数 r = 4 、相对磁导率 r =1 ,且当 t = 0 t = 0、z =1 8m 时,电场幅值为

10V/m。试求电场强度和磁场强度的瞬时表示式。 解:设电场强度的瞬时表示式为 E(=,1)=eE,=e,10cos(@t-k+) 式中0=2对=2πx103rads =am-吕-adn 对于余弦函数,当相角为零时达振幅值。考虑条件t=0、z=1/8m时,电场达到幅值,得 =北=经君 所以 c0-=10广co2a×101-经:+2 -a10cs2rx101-经e-g》Vm 月=×E=, 磁场强度的瞬时表示式为 =60m0 式中 e,0=g,0os2mx101-音e-g】n 104 因此 例5.1.4自由空间中平面波的电场强度 E=e.50cos(ot-k)V/m 求在=0处垂直穿过半径R=2.5m的圆平面的平均功率。 解:电场强度的复数表示式为E=E,50e大 自由空间的本征阻抗为 %=120π2 故得到该平面波的磁场强度 7
5 V m -4 10 。 试求电场强度和磁场强度的瞬时表示式。 解:设电场强度的瞬时表示式为 4 ( , ) 10 cos( ) x x x z t E t kz − E e e = = − + 式中 8 = = 2π 2π 10 rad/s f 8 r r 8 2π 10 4 4 π rad/m 3 10 3 k c = = = = 对于余弦函数,当相角为零时达振幅值。考虑条件 t = 0、z =1/8 m 时,电场达到幅值,得 4π 1 π 3 8 6 = = = kz 所以 4 8 4π π ( , ) 10 cos(2π 10 ) 3 6 E z t e t z x − = − + 4 8 4π 1 10 cos[2π 10 ( )] V/m 3 8 x e t z − = − − 磁场强度的瞬时表示式为 1 1 H e E e E z y x = = 式中 0 r 60π = = = 因此 4 10 4 1 8 ( , ) cos[2π 10 π( )] A/m 60π 3 8 H z t e t z y − = − − 例 5.1.4 自由空间中平面波的电场强度 E e t kz = − x 50cos( ) V/m 求在 0 z = z 处垂直穿过半径 R = 2.5m 的圆平面的平均功率。 解:电场强度的复数表示式为 j 50e kz E ex − = 自由空间的本征阻抗为 0 = 120π 故得到该平面波的磁场强度 j 0 5 e A/m 12π kz y y E H e e − = =
于是,平均坡印廷矢量 垂直穿过半径R=2.5m的圆平面的平均功率 g-5 ×π×2.52=65.1W 5.1.3沿任意方向传播的均匀平面波 沿+z方向传播的均匀平面波 沿传播方向的均匀平面波 E(=)=Ee-=Eewe.r E(F)=Eer=Ee5we k=ik k=ik=@k,+8ky+e.k e.Em =0 en·En=0 ie-xe) G)=e×E 等相位面 yxy,2头 波传播方向 沿任意方向传播的均匀平面波 例5.1.5在空气中传播的均匀平面波的磁场强度的复数表示式为 月=(-eA+e,2+e,4)e4 式中A为常数。求:(1)波矢量k:(2)波长和频率:(3)A的值:(4)相伴电场的复数形式: (5)平均坡印廷矢量。 解:()因为i=月.e”,所以
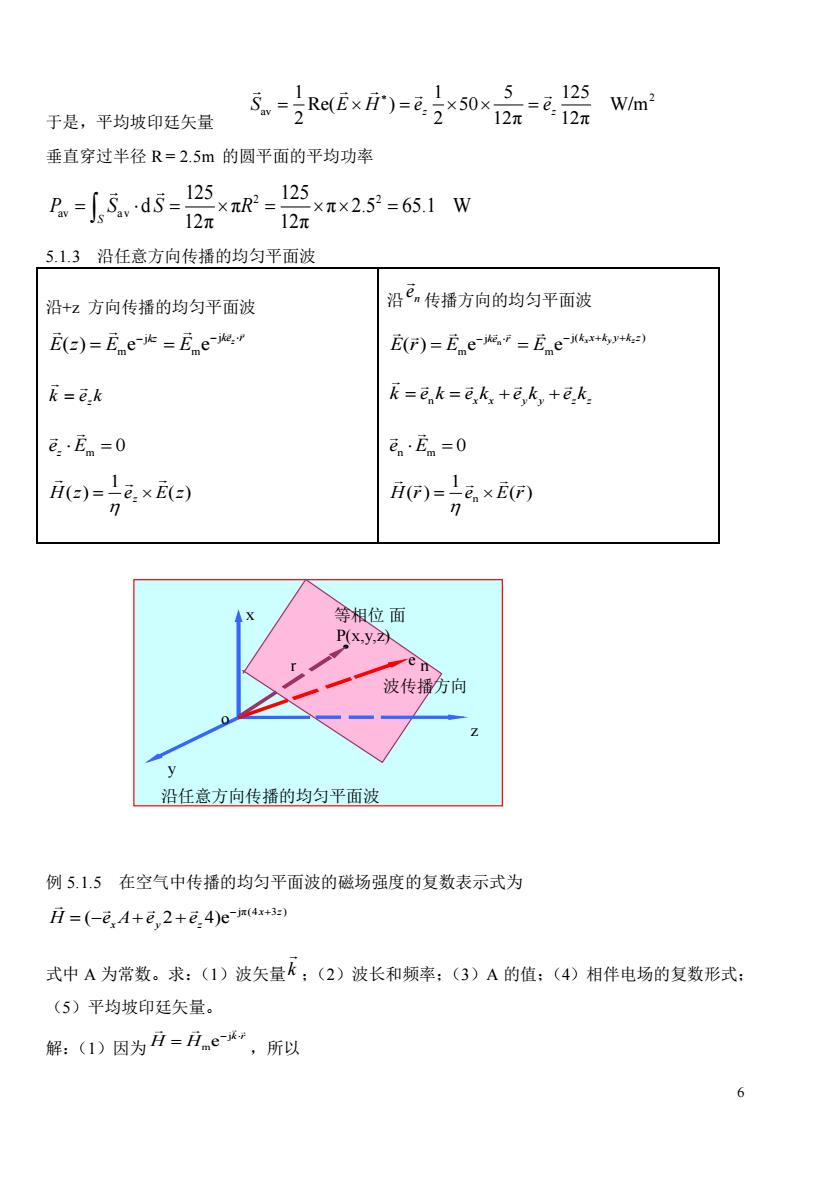
6 于是,平均坡印廷矢量 2 av 1 1 5 125 Re( ) 50 W/m 2 2 12π 12π z z S E H e e = = = 垂直穿过半径 R = 2.5m 的圆平面的平均功率 2 2 av a v 125 125 d π π 2.5 65.1 W S 12π 12π P S S R = = = = 5.1.3 沿任意方向传播的均匀平面波 沿+z 方向传播的均匀平面波 j j m m ( ) e e z kz ke r E z E E − − = = k e kz = e E z = m 0 ( ) 1 H(z) e E z z = 沿 n e 传播方向的均匀平面波 n j j( ) m m ( ) e e x y z ke r k x k y k z E r E E − − + + = = n x x y y z z k e k e k e k e k = = + + e E n m = 0 n 1 H r e E r ( ) ( ) = 例 5.1.5 在空气中传播的均匀平面波的磁场强度的复数表示式为 jπ(4 3 ) ( 2 4)e x z H e A e e x y z − + = − + + 式中 A 为常数。求:(1)波矢量 k ;(2)波长和频率;(3)A 的值;(4)相伴电场的复数形式; (5)平均坡印廷矢量。 解:(1)因为 j m e k r H H − = ,所以 沿任意方向传播的均匀平面波 波传播方向 z y x o r n e 等相位 面 P(x,y,z)

H=-@+2+e.4,k.F=kx+k y+k=4x+3 则k=4红、k,=0、k=3元,k=E,4红+E3π k=V(3π)2+(4π)}2=5元 。=反=已3+e3 1=2红-2红2 =7.5×10Hz (2) 3)K-月。=4-A0+0x2+3×4=0→,A=3 (4)E=nir)x元 =120m-e,3+,2+元4lem×尼号+e =120π(色,1.2+e5-1.6)e-4x+) 5=RelEx] =2Re120e,1.2+e,5-1.60e ×(-E,3+E,2+E4)em4*3:} (5) =12元×29×(e,4+e3)W/m2 5.2电磁波的极化 5.2.1极化的概念 5.2.2 线极化波 5.2.3 圆极化波 5.2.4 椭圆极化波 5.2.5 极化波的分解 5.2.6 极化波的工程应用 5.2.1极化的概念 波的极化在电磁波传播空间给定点处,电场强度矢量的端点随时间变化的轨迹。 波的极化表征在空间给定点上电场强度矢量的取向随时间变化的特性,是电磁理论中的一个重 要概念。 极化的三种形式 一般情况下,沿+:方向传播的均匀平面波E=E,E+,E,其中 E =E cos(ot-k+d),E=Eym cos(t-+)
7 m 2 4 H e e e = − + + x y z ,k r k x k y k z x z = + + = + x y z 4π 3π 则 4π 0 3π x y z k k k = = = 、 、 ,k e e = + x z 4π 3π 2 2 k = + = (3π) (4π) 5π n 4 3 x z 5 5 k e e e k = = + (2) 2π 2π 2 m k 5π 5 === , 7.5 10 Hz 2 / 5 3 10 8 8 = = = c f (3) m k H A = − + + = 4π( ) 0 2 3π 4 0 , A = 3 (4) 0 n E r H r e ( ) ( ) = jπ(4 3 ) jπ(4 3 ) 4 3 120π( 3 2 4)e ( ) 5 5 120π( 1.2 5 1.6)e x z x y z x z x z x y z e e e e e e e e − + − + = − + + + = + − (5) * av jπ (4 3 ) jπ (4 3 ) * 2 1 Re[ ] 2 1 Re 120π( 1.2 5 1.6)e 2 [( 3 2 4)e ] 12π 29 ( 4 3) W m x z x y z x z x y z x z S E H e e e e e e e e − + − + = = + − − + + = + 5.2 电磁波的极化 5.2.1 极化的概念 5.2.2 线极化波 5.2.3 圆极化波 5.2.4 椭圆极化波 5.2.5 极化波的分解 5.2.6 极化波的工程应用 5.2.1 极化的概念 波的极化 在电磁波传播空间给定点处,电场强度矢量的端点随时间变化的轨迹。 波的极化表征在空间给定点上电场强度矢量的取向随时间变化的特性, 是电磁理论中的一个重 要概念。 极化的三种形式 一般情况下,沿 + z 方向传播的均匀平面波 x x yEy E e E e = + ,其中 m cos( ) , E E t kz x x x = − + m cos( ) E E t kz y y y = − +

电磁波的极化状态取决于E,和B,的振幅之间和相位之间的关系,分为:线极化、圆极化、 椭圆极化。 线极化:电场强度矢量的端点轨迹为一直线段 圆极化:电场强度矢量的端点轨迹为一个圆 椭圆极化:电场强度矢量的端点轨迹为一个椭圆 5.2.2线极化波 条件:攻-月=0or±π 合成波电场的模 E=√E0,)+E0,)=√E+Ecos(o1+4)+-" 随时间变化 合成波电场与+x轴的夹角 a=arctan( E)=±arctan( 一一常数 Em 特点:合成波电场的大小随时间变化但其矢端,轨迹与x轴的夹角始终保持不变 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相位相同或相差 为士π时,其合成波为线极化波。 5.2.3圆极化波 条件 Em=Em=Em、4-4,=±π/2 则E,(0,)=Ecos(o1+4) 常数 E,(0,0=Ecos(o1+只于7=±E.sin(or+) 随时间变化 合成波电场的模 E=NE(0,)+E(0,)=E.4 合成波电场与+x轴的夹角 a=arctan[±tan(ot+,】=±(oi+g.) 特点:合成波电场的大小不随时间改变,但方向却随时间变化,电场的矢端在一个圆上并以角速 度0旋转。 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的振幅相同、相位 差为士12时,其合成波为圆极化波。 右旋圆极化波:若鸟-项=一x/2 则电场矢端的旋转方向与电磁波传播方向成右手螺旋关系, 称为右旋圆极化波 左旋圆极化波:若4=2,则电场矢端的旋转方向电磁波传播方向成左手螺旋关系,称 为左旋圆极化波
8 电磁波的极化状态取决于 Ex 和 Ey 的振幅之间和相位之间的关系,分为:线极化、圆极化、 椭圆极化。 线极化:电场强度矢量的端点轨迹为一直线段 圆极化:电场强度矢量的端点轨迹为一个圆 椭圆极化:电场强度矢量的端点轨迹为一个椭圆 5.2.2 线极化波 条件: x − y = 0 or 合成波电场的模 2 2 2 2 m m (0, ) (0, ) cos( ) E E t E t E E t = + = + + x y x y x 合成波电场与+ x 轴的夹角 m m arctan( ) arctan( ) y y x x E E E E = = 特点:合成波电场的大小随时间变化但其矢端,轨 迹与 x 轴的夹角始终保持不变 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相位相同或相差 为±π时,其合成波为线极化波。 5.2.3 圆极化波 条件 m m m π / 2 E E E x y x y = = − = 、 则 m (0, ) cos( ) E t E t x x = + m π (0, ) cos( ) sin( ) 2 E t E t E t y x m x = + = + 合成波电场的模 2 2 m (0, ) (0, ) E E t E t E = + = x y 合成波电场与+ x 轴的夹角 arctan[ tan( )] ( ) x x = + = + t t 特点:合成波电场的大小不随时间改变,但方向却随时间变化,电场的矢端在一个圆上并以角速 度ω 旋转。 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的振幅相同、相位 差为±π/ 2 时,其合成波为圆极化波。 右旋圆极化波:若 y −x = − 2 ,则电场矢端的旋转方向与电磁波传播方向成右手螺旋关系, 称为右旋圆极化波 左旋圆极化波:若 y −x = 2 ,则电场矢端的旋转方向电磁波传播方向成左手螺旋关系,称 为左旋圆极化波。 随时间变化 常数 常数 随时间变化

↑y 左旅隔杨化油 5.2.4椭圆极化波 其它情况下,令只一马,=少 由E,(0,)=Ecos(or+4) E(0,1)=E cos(ot+-) E.F,cos=sin' 可得到E'EEm 特点:合成波电场的大小和方向都随时间改变,其端点在一个椭圆上旋转。 合成波极化的小结 电磁波的极化状态取决于E,和E,的振幅E、E,-和相位差△0=?,一9
9 5.2.4 椭圆极化波 其它情况下,令 x − y = 由 m (0, ) cos( ) E t E t x x x = + m (0, ) cos( ) E t E t y y x = + − 可得到 2 2 2 2 2 m m m m 2 cos sin x y x y x y x y E E E E E E E E + − = 特点:合成波电场的大小和方向都随时间改变,其端点在一个椭圆上旋转。 合成波极化的小结 电磁波的极化状态取决于 Ex 和 Ey 的振幅 Exm、Eym 和相位差 = y −x 右旋圆极化波 o Ex y x Ey E a 左旋圆极化波 o x E y x y E E a

对于沿+z方向传播的均匀平面波: 线极化:△0=0、±π △0=0,在1、3象限:△0=±π,在2、4象限 圆极化:△0=±π2,E=E,n 取“十”,左旋圆极化:取“一”,右旋圆极化。 椭圆极化:其它情况。 0<A0<元,左旋:-<△0<0,右旋, 例5.2.1说明下列均匀平面波的极化方式。 (1)E=,E sin(-k)+,E cos(o-) (2)E=e,E.ek-e,jE.e ()或=0秀=受4的=受 (4)E-E sin(k)+,2E cos(o-) 解0)6。=6成=-受4=0,4的-受 左旋圆极化波 (2)EE,sin(cos(o 右旋圆极化波 线极化波 由感化微威民化流司分相 左旋椭圆极化波 任何一个线极化波都可以表示成旋向相反、振幅相等的两圆极化波的叠加,即 E=EE.e*=民+j记,)受c*+民-jg,)受e* 任何一个椭圆极化波也可以表示成旋向相反、振幅不等的两圆极化波的叠加,即 E=(,E+Em)e ((im e 2 5.2.6极化波的工程应用 电磁波的极化在许多领域中获得了广泛应用。如:
10 对于沿+ z 方向传播的均匀平面波: 线极化: = 0、 。 = 0 ,在 1、3 象限; = ,在 2、4 象限。 圆极化: = Exm = Eym 2, 取“+”,左旋圆极化;取“-”,右旋圆极化。 椭圆极化:其它情况。 0 ,左旋; − 0 ,右旋 。 例 5.2.1 说明下列均匀平面波的极化方式。 (1) m m sin( ) cos( ) E e E t kz e E t kz = − + − x y (2) j j m m e j e kz kz E e E e E x y − − = − (3) π π 0 , 2 2 x y = = − = − 、 (4) m m sin( ) 2 cos( ) E e E t kz e E t kz = − + − x y 解:(1) m m , E E x y = π π 0, 2 2 x y = − = = 、 (2) m m , E E x y = m m π π sin( ) cos( ) 4 4 E e E t kz e E t kz = − + + − − x y (3) π π , 0 4 4 x y = − = − = 、 (4) m m , E E x y π π 0, 2 2 x y = − = = 、 任何一个线极化波、圆极化波或椭圆极化波可分解成两个线极化波的叠加 任何一个线极化波都可以表示成旋向相反、振幅相等的两圆极化波的叠加,即 j j j m m m e ( j ) e ( j ) e 2 2 kz kz kz x x y x y E E E e E e e e e − − − = = + + − 任何一个椭圆极化波也可以表示成旋向相反、振幅不等的两圆极化波的叠加,即 j m m m m m m j j ( )e j j ( j) e ( j) e 2 2 kz x x y y x y x y kz kz x y x y E e E e E E E E E e e e e − − − = + + − = − + + 5.2.6 极化波的工程应用 电磁波的极化在许多领域中获得了广泛应用。如: 左旋圆极化波 右旋圆极化波 线极化波 左旋椭圆极化波