《电磁场理论》课程电子教案（讲义）第六章 均匀平面波的反射和透射

第6章均匀平面波的反射与透射 现象：电磁波入射到不同媒质分界面上时，一部分波被分界面反射， 一部分波透过分界面。 入射方式：垂直入射、斜入射： 媒质类型：理想导体、理想介质、导电媒质 分析方法： 边界条件 入射波（己知）十反射波（未知） 透射波（未知） 介质分界面 本音内容 6.1均匀平面波对分界面的垂直入射 6.2 均匀平面波对多层介质分界平面的垂直入射 6.3均匀平面波对理想介质分界平面的斜入射 6.4均匀平面波对理想导体表面的斜入射 6.1 均匀平面波对分界平面的垂直入射 本节内容 6.1.1对导电媒质分界面的垂直入射 6.12对理想导体表面的垂直入射 煤质1 煤质2 6.1.3对理想介质分界面的垂直入射 6.1.1对导电媒质分界面的垂直入射 均匀平面波垂直入射到两种不 z0中，导电媒质2的参数为%602 沿x方向极化的均匀平面波从媒质1垂直入射到与导电媒质2的分界平面上。 媒质1中的入射波 E,(e）=Eme-ni 片=jk。=jo√45e 媒质1： 蝶质2 ae)-e是e o(-) 6,4,1 6,4,0 媒质1中的反射波 E(=)=e,Eeni -品 H0◆ 日）=6， =n0-j总 媒质1中的合成波 E(=)=E()+E(=)=EEme-ni +e,Emenvi ,日=A(e)+i,(e)=8 Ee-， 媒质2中的透射波： E(e)=e,Ee,月.(e)=gEe 72e 为=达=joe=jo瓜u-j是

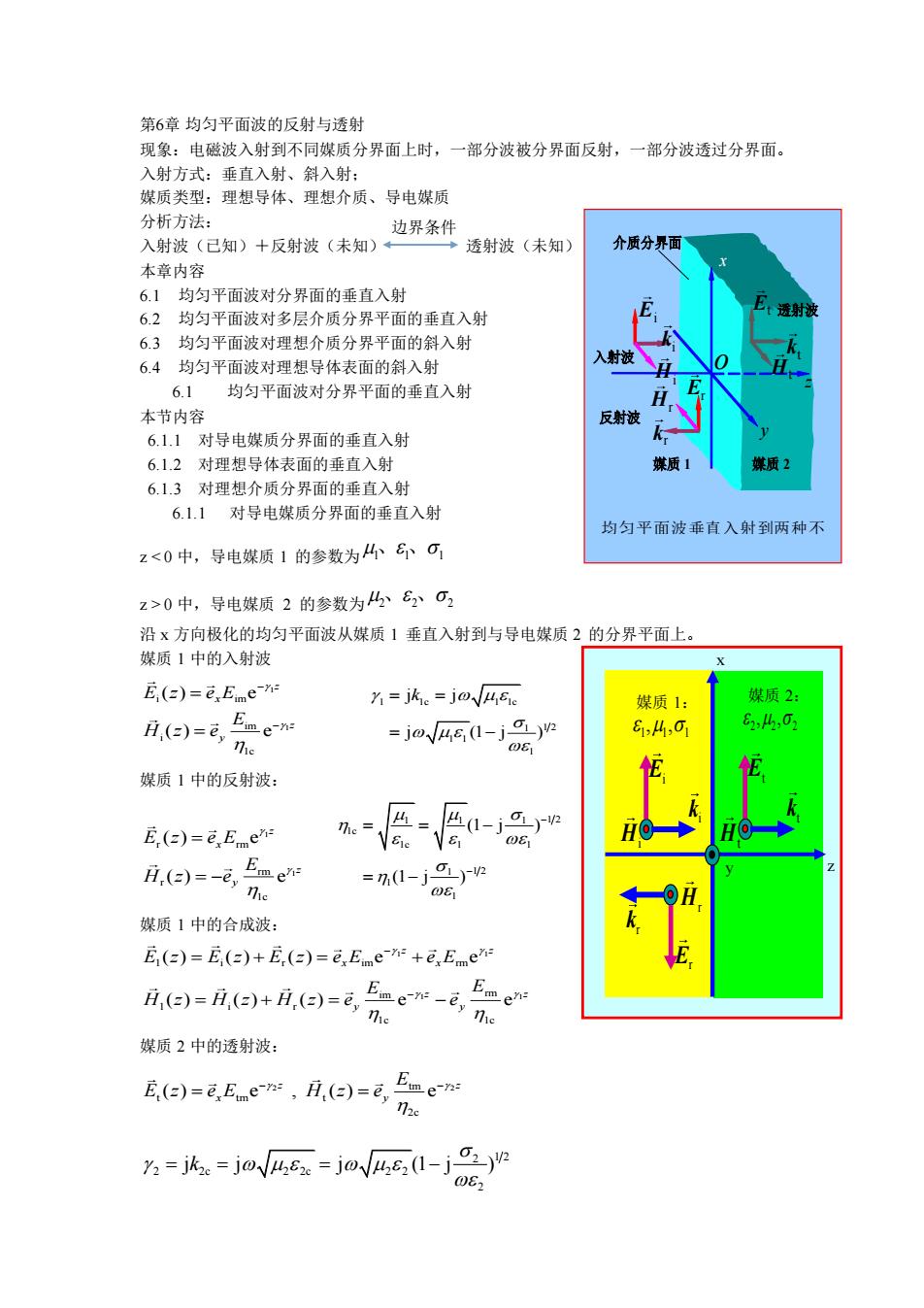
第6章 均匀平面波的反射与透射 现象：电磁波入射到不同媒质分界面上时，一部分波被分界面反射，一部分波透过分界面。 入射方式：垂直入射、斜入射； 媒质类型：理想导体、理想介质、导电媒质 分析方法： 入射波（已知）＋反射波（未知） 透射波（未知） 本章内容 6.1 均匀平面波对分界面的垂直入射 6.2 均匀平面波对多层介质分界平面的垂直入射 6.3 均匀平面波对理想介质分界平面的斜入射 6.4 均匀平面波对理想导体表面的斜入射 6.1 均匀平面波对分界平面的垂直入射 本节内容 6.1.1 对导电媒质分界面的垂直入射 6.1.2 对理想导体表面的垂直入射 6.1.3 对理想介质分界面的垂直入射 6.1.1 对导电媒质分界面的垂直入射 z 0 中，导电媒质 2 的参数为 2 2  2  、 、 沿 x 方向极化的均匀平面波从媒质 1 垂直入射到与导电媒质 2 的分界平面上。 媒质 1 中的入射波 1 1 i im im i 1c ( ) e ( ) e z x z y E z e E E H z e    − − = = 1 1c 1 1c 1 1 2 1 1 1 j j j (1 j )     k      = = = − 媒质 1 中的反射波： 1 1 r rm rm r 1c ( ) e ( ) e z x z y E z e E E H z e    = = − 1 1 1 1 2 1c 1c 1 1 1 1 2 1 1 (1 j ) (1 j )           − − = = − = − 媒质 1 中的合成波： 1 1 1 1 1 i r im rm im rm 1 i r 1c 1c ( ) ( ) ( ) e e ( ) ( ) ( ) e e z z x x z z y y E z E z E z e E e E E E H z H z H z e e       − − = + = + = + = − 媒质 2 中的透射波： 2 2 tm t tm t 2c ( ) e , ( ) e z z x y E E z e E H z e    − − = = 2 1 2 2 2c 2 2c 2 2 2 j j j (1 j ) k          = = = − 边界条件 均匀平面波垂直入射到两种不 同媒质的分界平面 入射波 反射波 介质分界面 Ei i k Er Hi Hr r k o z y x 媒质 1 媒质 2 Et Ht t k 透射波 z x 媒质 1： 媒质 2： 1 1 1  , , 2 2 2  , , y Ei Hi i k Er Hr r k Et Ht t k

在分界面z=0上，电场强度和磁场强度切向分量连续，即 「E(O)=E2(0) Em+Em =Eu H,(O)=H2(0) 定义分界面上的反射系数「为反射波电场的振幅与入射波电场振幅之比、透射系数π为 透射波电场的振幅与入射波电场振幅之比，则 Em+Em=Em F-Em=th-ths (Em-Em)= 1 212 2c E四 Em刀e+刀ie 讨论： 售上是数。表期反甜流和道销德的长和相位与入法不同 ()若媒质2为理想导体，即0，=0，则.=0，故有「=-1、t=0 ，=2 (④若两种媒质均为理想介质，即口=0=0，则得到 乃2+7 乃2+1 6.12对理想导体表面的垂直入射 媒质1为理想介质，G,=0 !在分界面上，反} 射波电场与入射 媒质2为理想导体，02=0 波电场的相位差 为 则A=,%-会%-0 故T=-l、t=0→Em=- E.(=)=2,Eme-iA:,H.(=)=e, Em.e-0 媒质1中的入射波： B.(2)-,:,F.(=)=g 5: 媒质1中的反射波： 媒质1中合成波的电磁场为 E(=)=2E (e-e)=-e,j2Em sin(B=) 月，(e）=e,E鱼(em:+e4)=E,2Ecos(B2

2 2 2 2 1 2 1 2 2c 2 2c 2 2 2 (1 j ) (1 j )           − − = = − = − 在分界面 z = 0 上，电场强度和磁场强度切向分量连续，即 定义分界面上的反射系数  为反射波电场的振幅与入射波电场振幅之比、透射系数  为 透射波电场的振幅与入射波电场振幅之比，则 讨论： (1) 1+ = (2)  和  是复数，表明反射波和透射波的振幅和相位与入射波都不同。 (3) 若媒质 2 为理想导体，即  2 =  ，则 2c = 0 ，故有  = −1、 = 0 (4) 若两种媒质均为理想介质，即 1 = 2 = 0 ，则得到 2 1 2 2 1 2 1 2 ,          − = = + + 6.1.2 对理想导体表面的垂直入射 媒质 1 为理想介质， 1 = 0 媒质 2 为理想导体，  2 =  则 1 1 1     = , 1 1 1 ,    = 2 = 0 故  = −1、 = 0 E E rm im = − 媒质 1 中的入射波： 1 1 j j im i im i 1 ( ) e , ( ) e z z x y E E z e E H z e    − − = = 媒质 1 中的反射波： 1 1 j j im r im r 1 ( ) e , ( ) e z z x y E E z e E H z e    = − = 媒质 1 中合成波的电磁场为 1 1 1 1 j j 1 im im 1 im im 1 j j 1 1 1 ( ) (e e ) j2 sin( ) 2 cos( ) ( ) (e e ) z z x x z z y y E z e E e E z E E z H z e e         − − = − = − = + = (0) (0) (0) (0) 1 2 1 2 H H E E =  =   im rm tm im rm tm 1c 2c 1 1 ( ) E E E E E E   + = − =    im rm tm im rm tm 1c 2c 1 1 ( ) E E E E E E   + = − =    tm 2c im 2c 1c E 2 E     = = + rm 2c 1c im 2c 1c E E      − = =  +   x 媒质 1： 媒质 2： 1 1 1  , ,  2 =  z z = 0 y Ei Hi i k Er Hr r k 在分界面上，反 射波电场与入射 波电场的相位差 为π

瞬时值形式 =5π/ E(,1)=RelE (=)ei]=e,2Em sin(B=) (-Rc[F,(c 合成波的平均能流密度矢量 及-4E×1=a-e2E。sm 成=π/2 理想导体表面上的感应电流 J=x H()-x 2Em cos()2 合成波的特点 ()媒质1中的合成波是驻波。电场振幅的最大值为2E,最小值为0：磁场振幅的最 大值为2E/m,最小值也为0. 2)电场被节点E,日的最小值的位置) RF=-m之m-200123 ()电场波腹点(E,(仁的最大值的位置) H 月m=-(2m+r/2→=-2n+3 4 (4)两相邻波节点之间任意两点的电场同相。同一波节点 ③)瓦、月在时间上有4的相移。 ⑥瓦、五在空间上错开4，电场的波腹（节）点正好是磁场的波节骏)点。 ()坡印廷矢量的平均值为零，不发生能量传输过程，仅在两个波节间进行电场能量和磁 场能的交换。 例6.1.1 均匀平面波沿+z方向传播， 其电场强度矢量为 E =e,100sin(@t-B=)+,200cos(@t-B=)V/m

瞬时值形式 j 1 1 im 1 j im 1 1 1 1 ( , ) Re[ ( )e ] 2 sin( )sin( ) 2 ( , ) Re[ ( )e ] cos( )cos( ) t x t y E z t E z e E z t E H z t H z e z t        = = = = 合成波的平均能流密度矢量 * * im 1 av 1 1 im 1 1 1 1 2 cos( ) Re[ ] Re j2 sin( ) 0 2 2 x y E z S E H e E z e        =  = −  =           理想导体表面上的感应电流 im 1 im n 1 0 0 1 1 2 cos( ) 2 ( ) | | S z z y z x E z E J e H z e e e    =  = −  = = = 合成波的特点 （1）媒质 1 中的合成波是驻波。电场振幅的最大值为 2Eim ，最小值为 0 ；磁场振幅的最 大值为 2Eim 1 ，最小值也为 0。 （2）电场波节点（ E (z) 1 的最小值的位置） 1 min  z n = − π 1 min 2 n z  = − (n = 0 ,1,2,3, .) (3) 电场波腹点（ E (z) 1 的最大值的位置） 1 min  z n = − + (2 1)π / 2 1 max (2 1) 4 n z +  = − (n = 0 ,1,2,3, .) (4) 两相邻波节点之间任意两点的电场同相。同一波节点两侧的电场反相。 (5) E1 H1   、 在时间上有  4 的相移。 (6) E1 H1   、 在空间上错开  4 ，电场的波腹（节）点正好是磁场的波节腹）点。 (7) 坡印廷矢量的平均值为零，不发生能量传输过程，仅在两个波节间进行电场能量和磁 场能的交换。 例 6.1.1 一均匀平面波沿+z 方向传播， 其电场强度矢量为 i E e t z e t z = − + − x y 100sin( ) 200cos( ) V/m     π 2 5π 4 π π 4

(1)求相伴的磁场强度： 介质 (2)若在传播方向上2=0处，放置一无限大 理想导体平板，求区域z<0中的电场强度和 场强度： (3)求理想导体板表面的电流密度。 解：(1)电场强度的复数表示 E.=100e-i-e+200e-in- 则 写成瞬时表达式 (,t)=Re[,(=)e] ,00cdw-pz)+,100co(-z at=0 a=5π/4成 (2)反射波的电场为 E,(z)=-el00ere-m2-e,200e: 反射波的磁场为 F.(x)200c+100gle) 在区域z<0的合成波电场和磁场分别为 E=E.+E.=-e.j200e-/sin(Bz)-e.j400sin(B=) 月=月+月-0aBrE2 (3)理想导体表面电流密度为 j、=-e×i1lo =E200e+e,40-e053+e106 。 6.1.3对理想介质分界面的垂直入射 设两种煤质均为理想介质，即0，=0：=0 X=j识=jo√46 则h=j识=j@√48

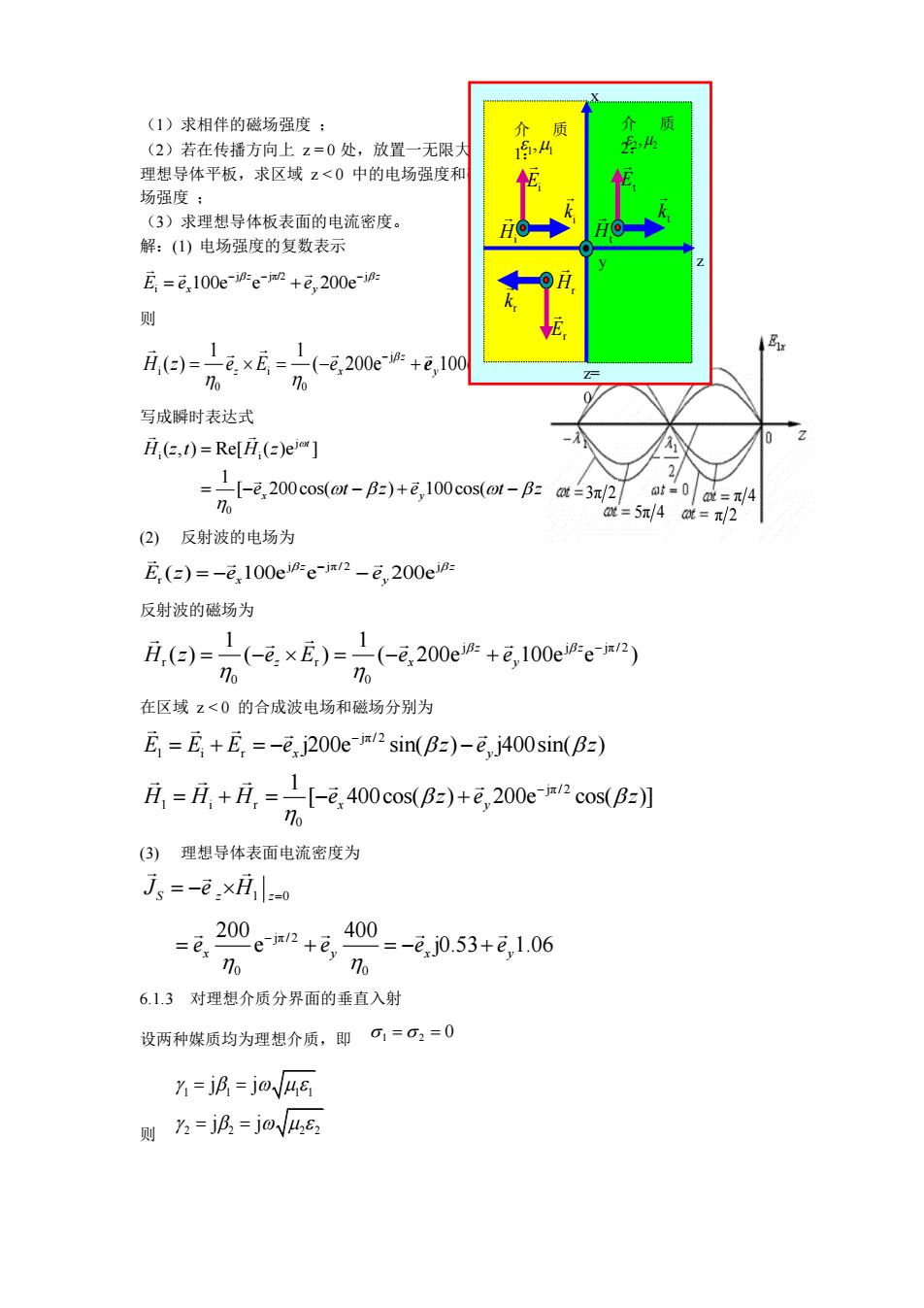
（1）求相伴的磁场强度 ； （2）若在传播方向上 z = 0 处，放置一无限大的 理想导体平板，求区域 z < 0 中的电场强度和磁 场强度 ； （3）求理想导体板表面的电流密度。 解：(1) 电场强度的复数表示 j jπ/2 j i 100e e 200e z z E e e x y − − −   = + 则 j j jπ/2 i i 0 0 1 1 ( ) ( 200e 100e e ) z z H z e E e z x y     − − − =  = − + e 写成瞬时表达式 j i i 0 ( , ) Re[ ( )e ] 1 1 [ 200cos( ) 100cos( π)] 2 t x y H z t H z e t z e t z       = = − − + − − (2) 反射波的电场为 j jπ/ 2 j r ( ) 100e e 200e z z E z e e x y   − = − − 反射波的磁场为 j j jπ/ 2 r r 0 0 1 1 ( ) ( ) ( 200e 100e e ) z z H z e E e e z x y     − = −  = − + 在区域 z < 0 的合成波电场和磁场分别为 jπ/ 2 1 i r jπ/ 2 1 i r 0 j200e sin( ) j400sin( ) 1 [ 400cos( ) 200e cos( )] x y x y E E E e z e z H H H e z e z      − − = + = − − = + = − + (3) 理想导体表面电流密度为 S z z 1 0 J e H = −  = jπ/ 2 0 0 200 400 e j0.53 1.06 x y x y e e e e   − = + = − + 6.1.3 对理想介质分界面的垂直入射 设两种媒质均为理想介质，即 1 = 2 = 0 则 1 1 1 1 2 2 2 2 j j j j           = = = = π 4 π 2 3π 2 5π 4 π 4 π 2 3π 2 5π 4 x 介 质 1： 介 质  1 ,1 2：2 2  , z z= 0 y Ei Hi i k Er Hr r k Et Ht t k

r设 讨论 (1)当>时，「>0，反射波电场与入射波电场同相。 (2)当乃<时，「<0，反射波电场与入射波电场反相。 E.(=)=,Eei: 媒质1中的入射波： e-e导c E.(=)=&: 1I,()-,rEa em. 媒质1中的反射波： E()=E()+E.(=) i,(）=i,()+i() 媒质1中的合成波： 11 E2(=)=E()=erE 月，(e)=月，(e)=gtEe: 媒质2中的透射波： 72 合成波的特点 E(=)=e E(e+r) -,E(1+)e:+r(e:-e) =eEim (1+)eit +j2rsin(B=) 这种由行波和纯驻波合成的波称为行驻波（混合波） 结电 一合成波电

1 2 1c 1 2c 2 1 2 ,         = = = = 2 1 2 2 1 2 1 2 ,          − = = + + 讨论 （1）当 2 1 时，   0 ，反射波电场与入射波电场同相。 （2）当 2 1 时，   0 ，反射波电场与入射波电场反相。 媒质 1 中的入射波： 1 1 j i im j im i 1 ( ) e ( ) e z x z y E z e E E H z e    − − = = 媒质 1 中的反射波： 1 1 j r im im j r 1 ( ) e ( ) e z x z y E z e E E H z e      = = − 媒质 1 中的合成波： 1 1 1 1 j j 1 i r im im j j 1 i r 1 ( ) ( ) ( ) (e e ) ( ) ( ) ( ) (e e ) z z x z z y E z E z E z e E E H z H z H z e        − − = + = + = + = − 媒质 2 中的透射波： 2 2 j 2 t im j im 2 t 2 ( ) ( ) e ( ) ( ) e z x z y E z E z e E E H z H z e      − − = = = = 合成波的特点 1 1 1 1 1 1 j j 1 im j j j im j im 1 ( ) (e e ) (1 )e (e e ) (1 )e j2 sin( ) z z x z z z x z x E z e E e E e E z             − − − − = + = + + −     = + +     这种由行波和纯驻波合成的波称为行驻波（混合波） 合成波电场振幅 (  0) 1 j2 2 1 im im 1 ( ) 1 e 1 2 cos(2 ) z E z E E z  = + = + +    —— 合成波电 场 —— 驻波电场 z —— 行波电场

当民.=-nr,即=-n/2(n=0,12,时，有 E(e以=El+ 当.=-(2m+π/2，即=-2+V4以=0，l2,时，有 E()=E1-n 92/472/452/432/42/4 合成波电 场振幅 合成波电 5元722九，3月 当月.=-nπ，即=-n/2n=0,12,.）时，有 E(e以=E1+ 当B.=-(2n+1)π/2.即=(n/2+4)月(=0,12时，有 E(e)=E1-n 92/47/452/432/4:2/4 合成波电 场振幅 合成波电 5/2221312元 212 E 1+r s→ 讨论

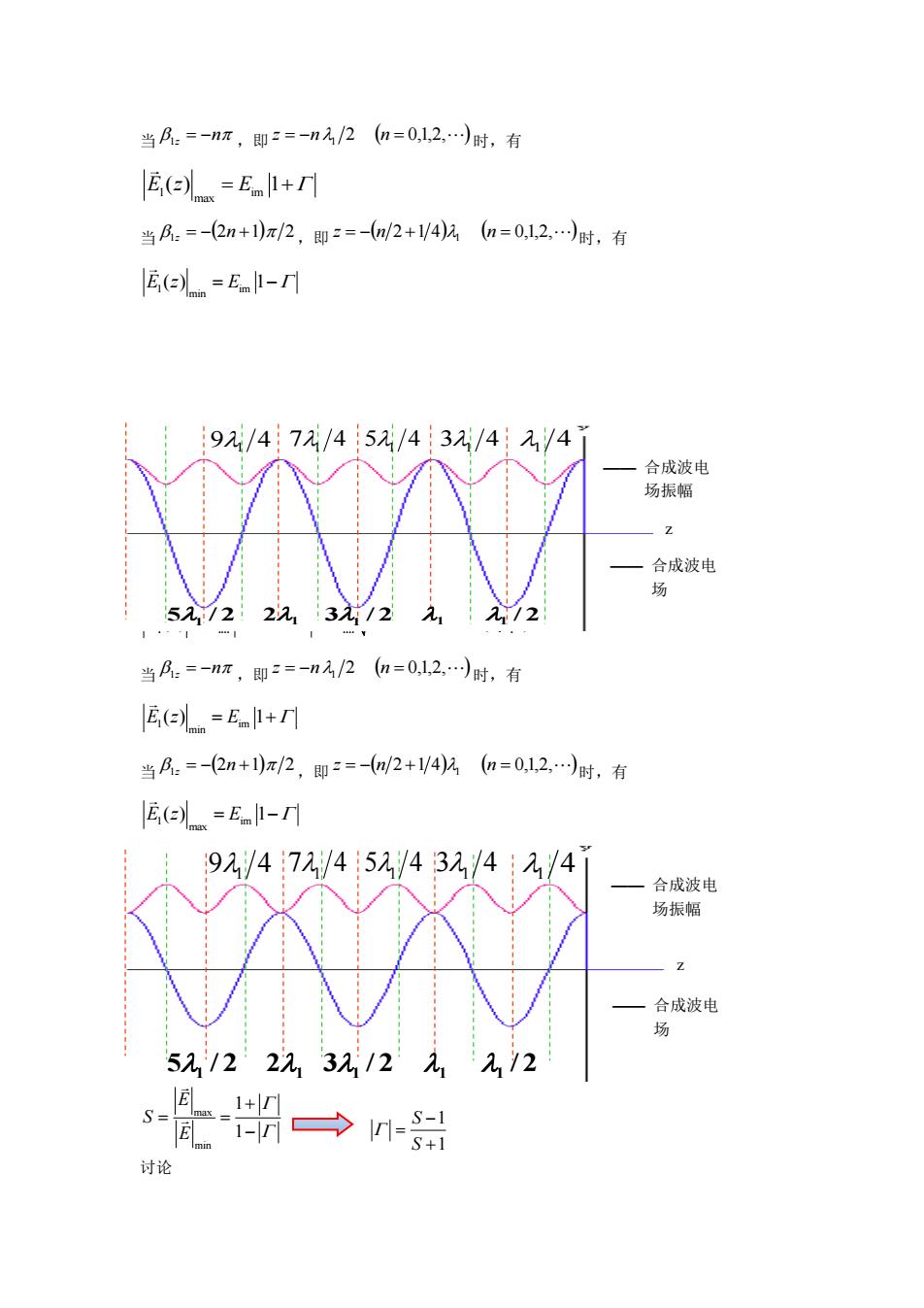
当 1z = −n ，即 2 ( 0,1,2, ) z = −n1 n = 时，有 1 im max E z E ( ) 1 = + 当 1z = −(2n +1) 2 ，即 ( 2 1 4) ( 0,1,2, ) z = − n + 1 n = 时，有 1 im min E z E ( ) 1 = − 合成波电场振幅 (  0) 1 j2 2 1 im im 1 ( ) 1 e 1 2 cos(2 ) z E z E E z  = + = + +     当 1z = −n ，即 2 ( 0,1,2, ) z = −n1 n = 时，有 1 im min E z E ( ) 1 = + 当 1z = −(2n +1) 2 ，即 ( 2 1 4) ( 0,1,2, ) z = − n + 1 n = 时，有 1 im max E z E ( ) 1 = − 驻波系数(驻波比) S 驻波系数 S 定义为驻波的电场强度振幅的最大值与最小值之比，即 max min 1 1 E S E   + = = − 1 1 + − = S S  讨论 51 / 2 21 31 / 2 1 1 / 2 91 4 71 4 51 4 31 4 1 4 —— 合成波电 场振幅 —— 合成波电 场 z 51 / 2 21 31 / 2 1 1 / 2 91 4 71 4 51 4 31 4 1 4 —— 合成波电 场振幅 —— 合成波电 场 z

当「=0时，S=1,为行波。 当「=士1时，S=0,是纯驻波。 当0<口<1时，1<S<0,为混合波。S越大，驻波分量越大，行被分量越小： 例6.12在自由空间，一均匀平面波垂直入射坐王阳土的工托个岳平而上已白由心 合成波的驻波比为3，介质内传输波的 电场的最小点。求介质的相对磁导率和相对介 ，a,=0 s=-3。 解：因为驻波比 1- H.H. T= 由于界面上是驻波电场的最小点，故 而反射系数 「-%-% :+n 式中 →%=%→丝-g 4=2 6=18t ◇ 又因为2区的波长 电磁能流密度 媒质1中沿工方向传播的平均密青套家 名应合 及-[医x]-玩品 入射波平均功率 密度减去反射波 及[]-吧rg [医]-e会- 媒质2中的平均功率密度 及[医]-绿r -r=+-n-路→8=8 由 72 例613入射波电场互=E100cos6x101-10xP/m,从空气(<0)中正入射到

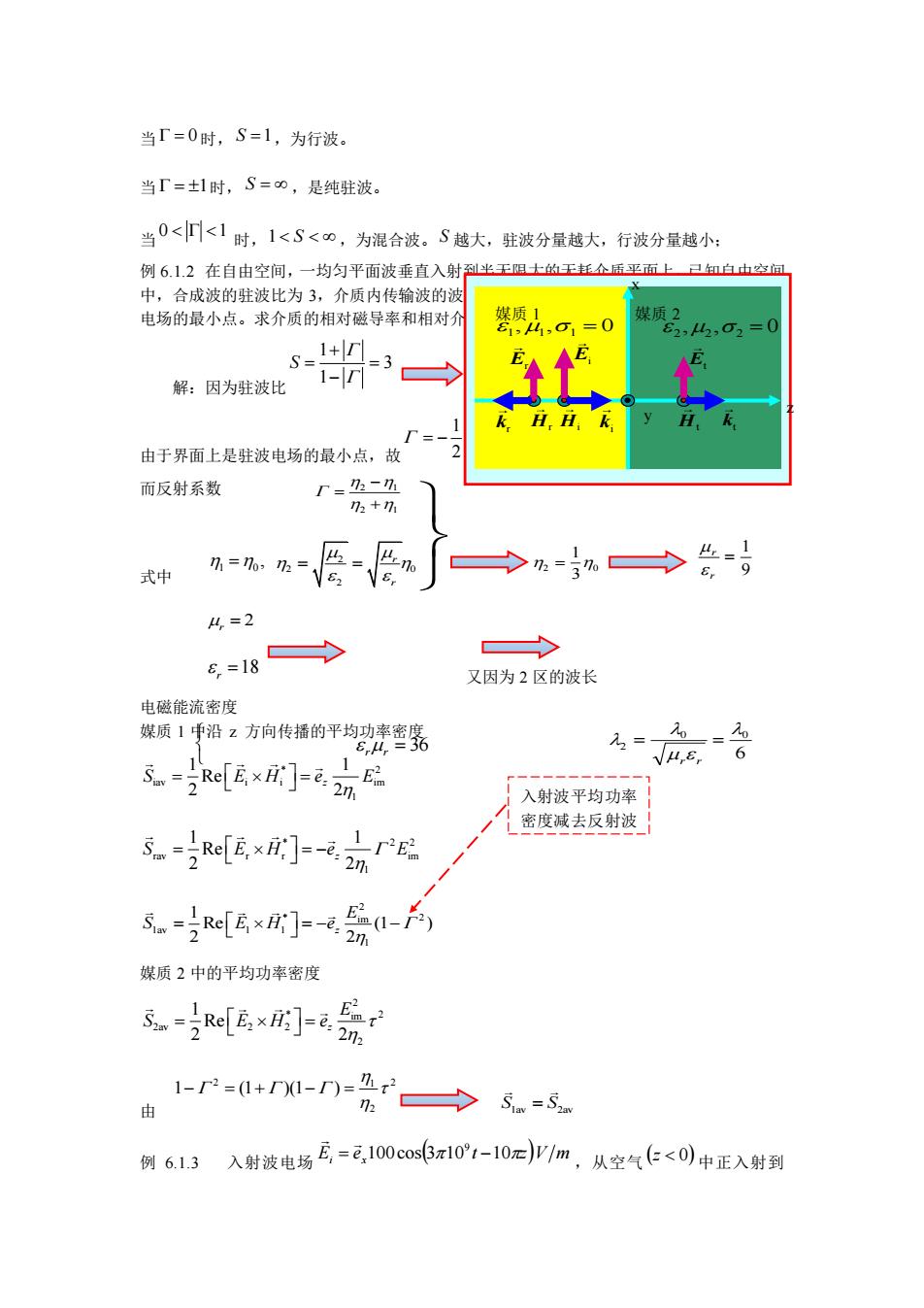
当  = 0 时， S =1 ，为行波。 当  = 1 时， S =  ，是纯驻波。 当 0   1 时， 1 S   ，为混合波。 S 越大，驻波分量越大，行波分量越小； 例 6.1.2 在自由空间，一均匀平面波垂直入射到半无限大的无耗介质平面上，已知自由空间 中，合成波的驻波比为 3，介质内传输波的波长是自由空间波长的 1/6，且分界面上为驻波 电场的最小点。求介质的相对磁导率和相对介电常数。 解：因为驻波比 1 3 1 S   + = = − 1 2  = 由于界面上是驻波电场的最小点，故 1 2  = − 而反射系数 式中 2 0 3 1  =  9 1 = r r   r = 2 18 r  = 又因为 2 区的波长 电磁能流密度 媒质 1 中沿 z 方向传播的平均功率密度 * 2 iav i i im 1 1 1 Re 2 2z S E H e E  =  =    * 2 2 rav r r im 1 1 1 Re 2 2z S E H e E   =  = −     2 * 2 im 1av 1 1 1 1 Re (1 ) 2 2z E S E H e   =  = − −     媒质 2 中的平均功率密度 2 * 2 im 2av 2 2 2 1 Re 2 2z E S E H e   =  =     由 2 2 1 2 1 (1 )(1 )       − = + − = S S 1av 2av = 例 6.1.3 入射波电场 Ei ex100cos(310 t 10z)V m 9 = −   ，从空气 (z  0) 中正入射到    2 1 2 1      − = + 1 0  = , 2 2 0 2 r r       = =     rr = 36 6 0 0 2      = = r r 入射波平均功率 密度减去反射波 平均功率密度 媒质 1 媒质 2  1 ,1 ,1 = 0  2 ,2 , 2 = 0 z x y Ei Hi ki Er kr Hr Et Ht kt

:=0的平面边界面上。在：>0区域中，4，=1、6，=4。求区域：>0的电场和磁场 解：2>0区域的本征阻抗 - _120m=60m0 2 透射系数 0 2×60π 相位常数 黄A=ao5-ga=2mn E,=eE cos(ot-B,=)=&tE cos(at-B,) =E0.667×10cos(3π×10°1-20元e) =e,6.67cos(3π×10°1-20me)V/m -22n01-0 =e,0.036cos(3π×10't-20元c)AWm 例6.14已知媒质1的5=441=10=0：媒质2的62=104：=40，=0 角频率)=5xI0ad小的均匀平面波从媒质1垂直入射到分界面上，设入射波是沿x轴 方向的线极化波，在1=0、：=0时，入射波电场的振幅为24/m。求： ()B和B: (2)反射系数和「： (3)1区的电场E(6,), (42区的电场E,(,)。 解：1) 月=a所a所瓜-ig2-33m

z = 0 的平面边界面上。在 z  0 区域中， r =1 、 r = 4 。求区域 z  0 的电场和磁场 。 解：z > 0 区域的本征阻抗 2 r2 2 0 2 r2 120π 60π Ω 2       = = = = 透射系数 2 1 2 2 2 60π 0.667 120π 60π      = = = + + 相位常数 故 9 2 2 2 0 0 r2 8 3π 10 2 20π rad/m 3 10          = = =  =  2 2m 2 im 2 9 9 cos( ) cos( ) 0.667 10cos(3π 10 20π ) 6.67cos(3π 10 20π ) V/m x x x x E e E t z e E t z e t z e t z = − = −      =   − =  − 2 2 2 9 9 1 6.67 cos(3π 10 20π ) 60π 0.036cos(3π 10 20π ) A/m z y y H e E e t z e t z  =  =  − =  − 例 6.1.4 已知媒质 1 的  r1 = 4、r1 =1、1 = 0 ；媒质 2 的  r 2 =10、r 2 = 4、 2 = 0。 角频率 rad s 8  = 510 的均匀平面波从媒质 1 垂直入射到分界面上，设入射波是沿 x 轴 方向的线极化波，在 t = 0、z = 0 时，入射波电场的振幅为 2.4V m 。求： (1) 1 和  2 ； (2) 反射系数 1 和 2 ； (3) 1 区的电场 E (z,t) 1  ； (4) 2 区的电场 E (z,t) 2  。 解:（1） 8 1 1 1 0 0 r1 r1 8 5 10 2 3.33 rad/m 3 10           = = =  = 

oi-10st aum 4-悟n层=对mn 4 1-%设-8901n 2+ (3)1区的电场 E(=)=E(=)+E(=)=e,E(ei+Te ,E[(1+e:+j2rsin(B)] =E2.4[1.117e-33:+j0.234sin(3.33z】 或E(e)=E(e)+E,(e)=e,2.4eB:+E,0.281e E(=,t)=Re E(=)eia =e,2.4cos(5×10t-3.33)+e.0.281c0s(5×10t+3.33z) T= 2n2≈1.12 (4) n+2 E.(=)=e,Eue in:=,rEmne-ins: =,1.12×2.4e1054:=g,2.68e054 E2(z,1)=e2.68cos(5×1031-10.54z) 不为物平面技对多层分喷分界平面的香面入时 62.1多层介质中的场量关系与等效波阻抗 6.2.2四分之一波长匹配层 6.2.3半波长介质窗 62.1多层介质中的场量关系与等效波阻抗 电磁波在多层介质中的传播具有普遍的实际意义。 以三种介质形成的多层媒质为例，说明平面波在多层媒质中的传播过程及其求解方法。 如图所示，当平面波自媒质①向分界面垂直入射时，在媒质①和②之间的分界面上发生 反射和透射。当透射波到达媒质②和③的分界面时，又发生反射与透射，而且此分界面上的

8 2 0 0 r2 r2 8 5 10 10 4 10.54 rad/m 3 10        = =  =  （2） 1 r1 1 0 0 1 r1 1 60π Ω 2        = = = = 2 r2 2 0 0 2 r2 4 75.9π Ω 10        = = = 0.117 60 75.9 75.9 60 2 1 2 1 = + − = + − =      （3） 1 区的电场 1 1 1 j j 1 i r im j im 1 j3.33 ( ) ( ) ( ) (e e ) [(1 )e j2 sin( )] 2.4[1.117e j0.234sin(3.33 )] z z x z x z x E z E z E z e E e E z e z        − − − = + = + = + + = + 或 j3.33 j3.33 1 i r ( ) ( ) ( ) 2.4e 0.281e z z E z E z E z e e x x − = + = + j 1 1 8 8 ( , ) Re ( )e 2.4cos(5 10 3.33 ) 0.281cos(5 10 3.33 ) t x x E z t E z e t z e t z  =     =  − +  + （4） 1.12 2 1 2 2  + =     故 2 2 j j 2 tm im ( ) e e z z E z e E e E x x    − − = = j10.54 j10.54 1.12 2.4e 2.68e z z x x e e − − =  = 8 2 ( , ) 2.68cos(5 10 10.54 ) E z t e t z =  − x 6.2 均匀平面波对多层介质分界平面的垂直入射 本节内容 6.2.1 多层介质中的场量关系与等效波阻抗 6.2.2 四分之一波长匹配层 6.2.3 半波长介质窗 6.2.1 多层介质中的场量关系与等效波阻抗 电磁波在多层介质中的传播具有普遍的实际意义。 以三种介质形成的多层媒质为例，说明平面波在多层媒质中的传播过程及其求解方法。 如图所示，当平面波自媒质①向分界面垂直入射时，在媒质①和②之间的分界面上发生 反射和透射。当透射波到达媒质②和③的分界面时，又发生反射与透射，而且此分界面上的

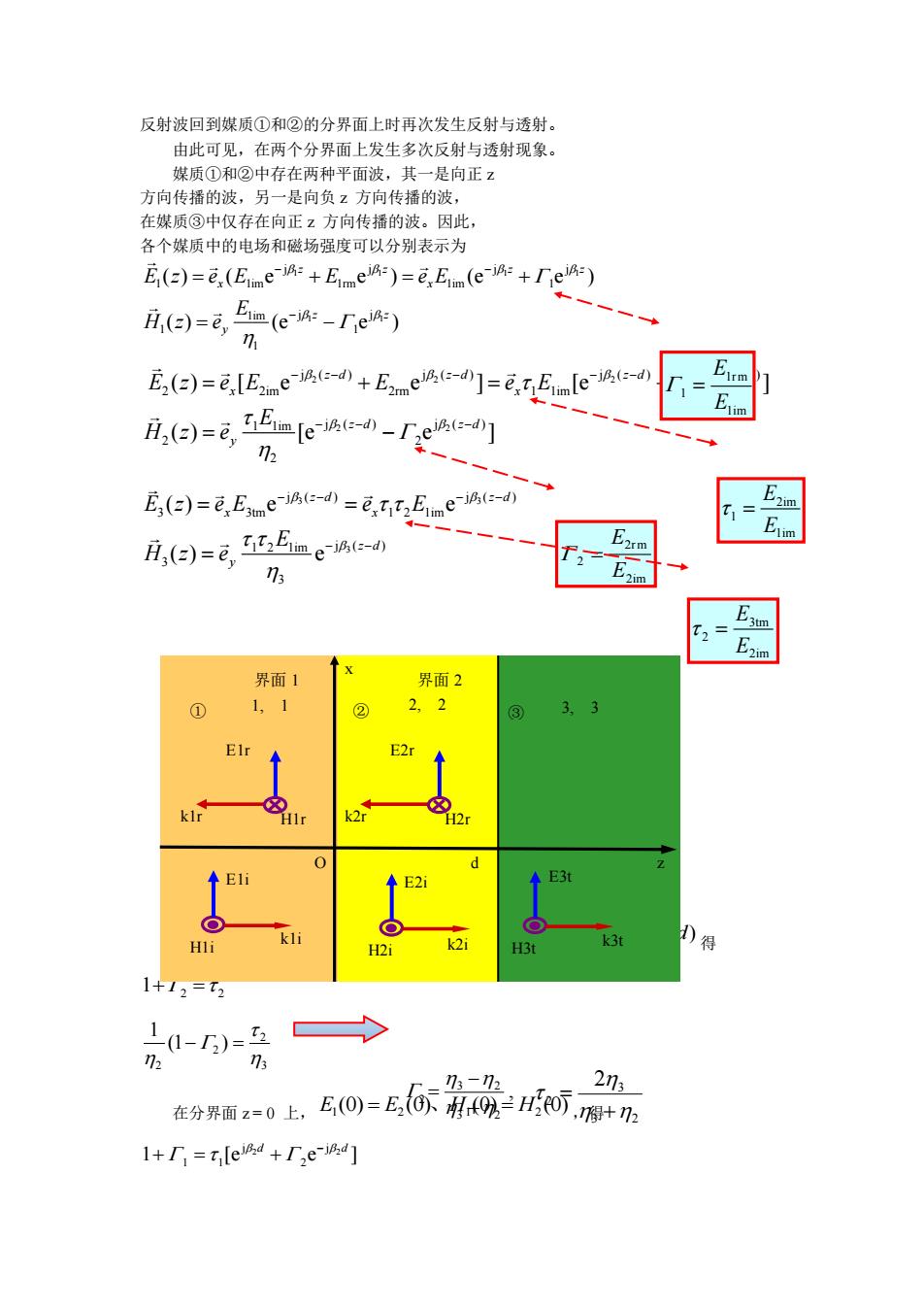
反射波回到媒质①和②的分界面上时再次发生反射与透射。 由此可见，在两个分界面上发生多次反射与透射现象， 媒质①和②中存在两种平面波，其一是向正乙 方向传播的波，另一是向负z方向传播的波， 在媒质③中仅存在向正z方向传播的波。因此， 各个媒质中的电场和磁场强度可以分别表示为 E(=)=e,()=E() i,(e)=e,e4-re4) E(),[EmEmle 月，e)=e5ea-f,ee] E()=Ee)) E 月，（日）=E,5me4e E3四 界面2 3.3 1+12=2 273 在分面z=0上.EO)=E帮4外0，形+n 1+D=tled+厂，eiu]

反射波回到媒质①和②的分界面上时再次发生反射与透射。 由此可见，在两个分界面上发生多次反射与透射现象。 媒质①和②中存在两种平面波，其一是向正 z 方向传播的波，另一是向负 z 方向传播的波， 在媒质③中仅存在向正 z 方向传播的波。因此， 各个媒质中的电场和磁场强度可以分别表示为 1 1 1 1 1 1 j j j j 1 1im 1rm 1im 1 1im j j 1 1 1 ( ) ( e e ) (e e ) ( ) (e e ) z z z z x x z z y E z e E E e E E H z e          − − − = + = + = − 2 2 2 2 2 2 j ( ) j ( ) j ( ) j ( ) 2 2im 2rm 1 1im 2 1 1im j ( ) j ( ) 2 2 2 ( ) [ e e ] [e e ] ( ) [e e ] z d z d z d z d x x z d z d y E z e E E e E E H z e            − − − − − − − − − = + = + = − 3 3 3 j ( ) j ( ) 3 3tm 1 2 1im 1 2 1im j ( ) 3 3 ( ) e e ( ) e z d z d x x z d y E z e E e E E H z e         − − − − − − = = = 根据边界条件，在分界面 z = d 上 ， ( ) ( ) ( ) ( ) E2 d = E3 d 、H2 d = H3 d 得 1 2 2 + = 3 2 2 2 (1 ) 1     − = 在分界面 z = 0 上， (0) (0) (0) (0) E1 = E2 、H1 = H2 ，得 2 2 j j 1 1 2 1 [e e ]   d d    − + = + O d z ① 1, 1 ② ③ k1i H1i E1i k1r H2i E2i k2i E1r H1r k2r E2r H2r k3t H3t E3t 2, 2 3, 3 x 界面 1 界面 2 1r m 1 1im E E  = 2im 1 1im E E  = 2r m 2 2im E E  = 3tm 2 2im E E  = , 3 2 3 2 2      + − = 3 2 3 2 2     + =