
第四章时变电磁场 本章内容 41 波动方程 42 电磁场的位函数 4.3 电磁能量守恒定律 44 惟一性定理 4.5 时谐电磁场 1波动方程 1.问题的提出: 麦克斯韦方程 ,一阶矢量微分方程组,描述电场与磁场间的相互作用关系。 波动方程 ,二阶矢量微分方程,揭示电磁场的波动性 麦克斯韦方程组 波动方程。 2.无源区的波动方程 在无源空间中,设媒质是线性、各向同性且无损耗的均匀媒质,则有电磁波动方程: V2E-4 8E =0 n=0 -ar 推证 Vxh=6OE aH v.月=0 V.E=0 vxvx月=Vx(eE) 所-n=-4e0a 同理可得 v-m50 3问题: 若为有源空间,结果如何?若为导电媒质,结果如何 4.2 电磁场的位函数
1 2 2 ( ) t H H H − = − 2 0 2 2 2 = − t H H 第四章 时变电磁场 本章内容 4.1 波动方程 4.2 电磁场的位函数 4.3 电磁能量守恒定律 4.4 惟一性定理 4.5 时谐电磁场 .1 波动方程 1.问题的提出: 麦克斯韦方程 —— 一阶矢量微分方程组,描述电场与磁场间的相互作用关系。 波动方程 —— 二阶矢量微分方程,揭示电磁场的波动性。 麦克斯韦方程组 波动方程。 2.无源区的波动方程 在无源空间中,设媒质是线性、各向同性且无损耗的均匀媒质,则有电磁波动方程: 0 2 2 2 = − t E E 0 2 2 2 = − t H H 推证 = = = − = 0 0 Ε H t H Ε t Ε H 同理可得 0 2 2 2 = − t E E 3.问题: 若为有源空间,结果如何?若为导电媒质,结果如何? 4.2 电磁场的位函数 ( ) t E H =

讨论内容:位函数的定义位函数的性质位函数的规范条件位函数的微分方程 1.引入位函数的意义 引入位函数来描述时变电磁场,使一些问题的分析得到简化。 2.位函数的定义 V.D=p V.B=0→B=V×A a D=sE、E= VxE=. aB -Vo)=P A at→ V×(E+sw.(-a1 -Vo 3.位函数的不确定性 -v.A+4s2=0 满足下列变换关系的两组位函数和中能描述同一个电憾场慰。刀任意可微函数 [=A+Vw p-ug=-2 aw 0=p-a V×A=V×(A+Vw)=V×A -vo:-04-v(9-ov)-3(A+9w)- aA 也就是说,对一给定的电磁场可用不同的位函数来描述。 不同位函数之间的上述变换称为规范变换。 原因:未规定A的散度。 4.位函数的规范条件 造成位函数的不确定性的原因就是没有规定A的散度。利用位函数的不确定性,可通过规定A的 散度使位函数满足的方程得以简化 在电磁理论中,通常采用洛仑兹条件,即 .+-0 除了利用洛仑兹条件外,另一种常用的是库仑条件,即 7.A=0 5.位函数的微分方程 同样 2a-9m0 =- at
2 讨论内容:位函数的定义 位函数的性质 位函数的规范条件 位函数的微分方程 1.引入位函数的意义 引入位函数来描述时变电磁场,使一些问题的分析得到简化。 2.位函数的定义 B = 0 B A = t B Ε = − ( ) = 0 + t A Ε − = − t A E 3.位函数的不确定性 满足下列变换关系的两组位函数 A 和Φ 能描述同一个电磁场问题。Φ为任意可微函数 A A t = + = − 即: ( ) ( ) ( ) A A A A A A t t t t = + = − − = − − − + = − − 也就是说,对一给定的电磁场可用不同的位函数来描述。 不同位函数之间的上述变换称为规范变换。 原因:未规定 → A 的散度。 4.位函数的规范条件 造成位函数的不确定性的原因就是没有规定 → A 的散度。利用位函数的不确定性,可通过规定 → A 的 散度使位函数满足的方程得以简化。 在电磁理论中,通常采用洛仑兹条件,即 = 0 + t A 除了利用洛仑兹条件外,另一种常用的是库仑条件,即 A = 0 5. 位函数的微分方程 同样 = − − 2 2 2 t J t A A = − − 2 2 2 D = − = = − t A D E E 、 − = (− ) t A = 0 + t A = − − 2 2 2 t

6.说明 a应用洛仑兹条件的特点:①位函数满足的方程在形式上是对称的,且比较简单,易求解: ②解的物理意义非常清楚,明确地反映出电磁场具有有限的传递速度:③矢量位只决定于 J,标量位只决定于P,这对求解方程特别有利。只需解出A,无需解出P就可得到待求的 电场和磁场。 b.电磁位函数只是简化时变电磁场分析求解的一种辅助函数,应用不同的规范条件,矢量位A 和标量位P的解也不相同,但最终得到的电磁场矢量是相同的。 7.问题 若应用库仑条件,位函数满足什么样的方程?具有什么特点? 4.3电磁能量守恒定律 讨论内容:电磁能量及守恒关系;坡印廷定理;坡印廷矢量 1.电磁能量及守恒关系 电场能量密度,收-万 磁场能量密度: ”-B 电疆能量密度,=+=E.+H,B 空间区域V中的电磁能量 =可nmr=j,ED+HaW 特点:当场随时间变化时,空间各点的电磁场能量密度也要随 时间改变,从而引起电磁能量流动。 电磁能量守恒关系: 进入体积V的能量=体积V内增加的能量+体积V内损耗的能量 2.坡印廷定理 表征电磁能量守恒关系的定理 0(E.D+B+E-J 微分形式: -v.(E×m=a5 积分形式: -医xma5-.0+n-a+Eja 2
3 6.说明 a. 应用洛仑兹条件的特点:① 位函数满足的方程在形式上是对称的,且比较简单,易求解; ② 解的物理意义非常清楚,明确地反映出电磁场具有有限的传递速度;③ 矢量位只决定于 J,标量位只决定于ρ,这对求解方程特别有利。只需解出 A,无需解出 就可得到待求的 电场和磁场。 b. 电磁位函数只是简化时变电磁场分析求解的一种辅助函数,应用不同的规范条件,矢量位 A 和标量位 的解也不相同,但最终得到的电磁场矢量是相同的。 7.问题 若应用库仑条件,位函数满足什么样的方程? 具有什么特点? 4.3 电磁能量守恒定律 讨论内容:电磁能量及守恒关系; 坡印廷定理; 坡印廷矢量 1. 电磁能量及守恒关系 电场能量密度: e 1 2 w = E D 磁场能量密度: m 1 2 w = H B 电磁能量密度: e m 1 1 2 2 w w w E D = + = + H B 空间区域 V 中的电磁能量: 1 1 d ( )d V V 2 2 W w V E D H B V = = + 特点:当场随时间变化时,空间各点的电磁场能量密度也要随 时间改变,从而引起电磁能量流动。 电磁能量守恒关系: 进入体积 V 的能量=体积 V 内增加的能量+体积 V 内损耗的能量 2. 坡印廷定理 表征电磁能量守恒关系的定理 微分形式: E D H B E J t E H + + − = ) 2 1 2 1 ( ) ( 积分形式: − = + + S V V E D H B V E J V t E H S )d d 2 1 2 1 ( d d ( ) d

.写e0raar SE.Jav -f.(E×H)d 通过曲面S进入体积V的电磁功率。 推证 P×A=了+0 E.v×月=Ej+E.0 由 at x0 月.vxE=-月.明 将以上两式相减,得到 E.vx月-月vxE=E.j+E.D+月.通 在线性和各向同性的媒质中,当参数都不随时间变化时,则有 E.V×H-H.7×E=-7.(E×而 E.OD-E.OE1(E.E)(E.D) 月. -明.0=uA面-0A =24 8t2 再利用矢量恒等式: 即可得到坡印廷定理的微分形式: -V(E×H)= -8ErnE 在任意闭曲面S所包围的体积V上,对上式两瑞积分,并应用散度定理,即可得到坡印廷定理
4 其中: + V E D H B V t )d 2 1 2 1 ( d d V E J dV − S E H S ( ) d 通过曲面 S 进入体积 V 的电磁功率。 推证 = − = + t B Ε t D H J 将以上两式相减,得到 t B H t D Ε H H Ε Ε J Ε + − = + 在线性和各向同性的媒质中,当参数都不随时间变化时,则有 ) 2 1 ( ( ) 2 1 Ε D t t Ε Ε t Ε Ε t D Ε = = = ) 2 1 ( ( ) 2 1 H B t t H H t H H t B H = = = 再利用矢量恒等式: 即可得到坡印廷定理的微分形式: Ε D H B Ε J t Ε H + + − = ) 2 1 2 1 ( ) ( 在任意闭曲面 S 所包围的体积 V 上,对上式两端积分,并应用散度定理,即可得到坡印廷定理 由 = − = + t B H Ε H t D Ε H Ε J Ε Ε H H Ε (Ε H) − = −
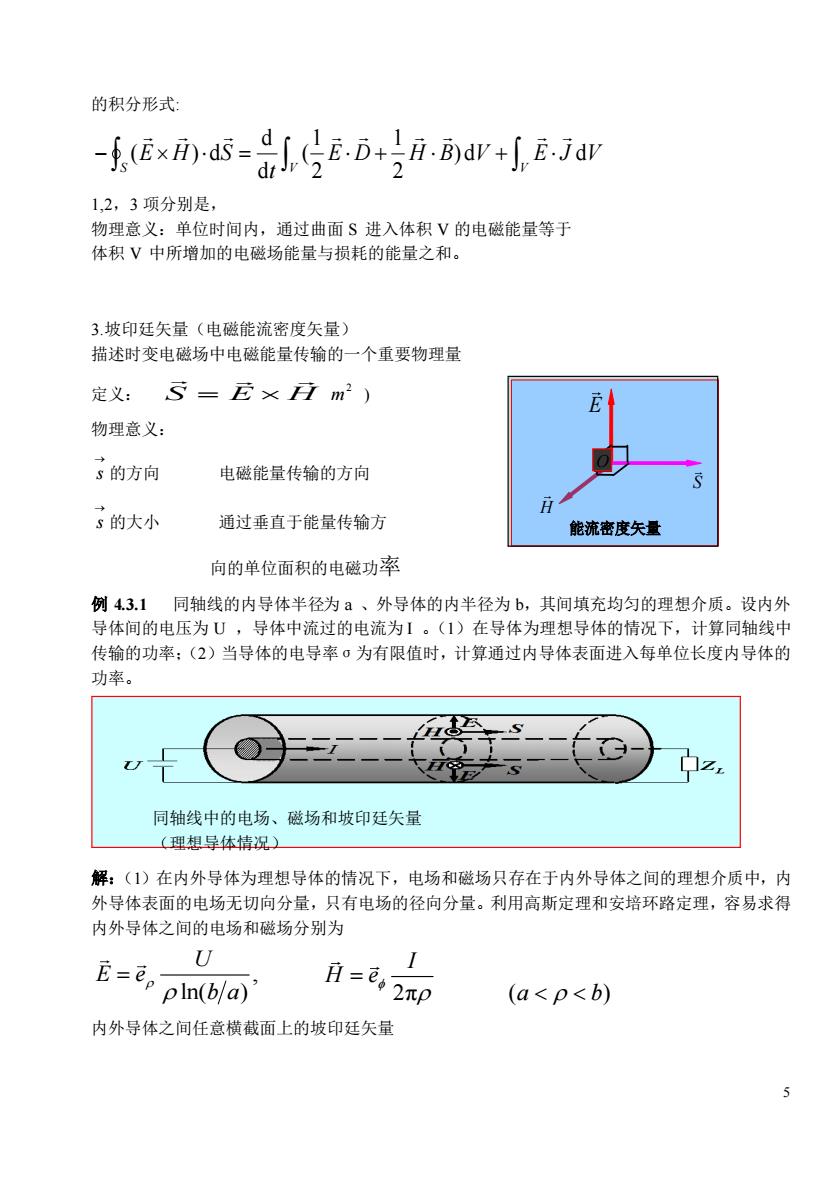
的积分形式 -f (ExH)-dS=d[(E.D+H.Bdv+[E.Jdv 12,3项分别是, 物理意义:单位时间内,通过曲面S进入体积V的电磁能量等于 体积V中所增加的电磁场能量与损耗的能量之和。 3.坡印廷矢量(电磁能流密度矢量) 描述时变电磁场中电磁能量传输的一个重要物理量 定义:5=E×方m2) 物理意义: 3的方向 电磁能量传输的方向 S的大小 通过垂直于能量传输方 能流密度矢量 向的单位面积的电磁功率 例43.1同轴线的内导体半径为a、外导体的内半径为b,其间填充均匀的理想介质。设内外 导体间的电压为U,导体中流过的电流为。(1)在导体为理想导体的情况下,计算同轴线中 传输的功率:(2)当导体的电导率σ为有限值时,计算通过内导体表面进入每单位长度内导体的 功率。 同轴线中的电场、磁场和坡印廷矢量 (理想导体情况) 解:(1)在内外导体为理想导体的情况下,电场和磁场只存在于内外导体之间的理想介质中,内 外导体表面的电场无切向分量,只有电场的径向分量。利用高斯定理和安培环路定理,容易求得 内外导体之间的电场和磁场分别为 U E=2 pin(bla) i=色,2p (a<p<b) 内外导体之间任意横截面上的坡印廷矢量
5 的积分形式: − = + + S V V E D H B V E J V t E H S )d d 2 1 2 1 ( d d ( ) d 1,2,3 项分别是, 物理意义:单位时间内,通过曲面 S 进入体积 V 的电磁能量等于 体积 V 中所增加的电磁场能量与损耗的能量之和。 3.坡印廷矢量(电磁能流密度矢量) 描述时变电磁场中电磁能量传输的一个重要物理量 定义: ( W/ 2 m ) 物理意义: → s 的方向 电磁能量传输的方向 → s 的大小 通过垂直于能量传输方 向的单位面积的电磁功率 例 4.3.1 同轴线的内导体半径为 a 、外导体的内半径为 b,其间填充均匀的理想介质。设内外 导体间的电压为 U ,导体中流过的电流为 I 。(1)在导体为理想导体的情况下,计算同轴线中 传输的功率;(2)当导体的电导率σ为有限值时,计算通过内导体表面进入每单位长度内导体的 功率。 解:(1)在内外导体为理想导体的情况下,电场和磁场只存在于内外导体之间的理想介质中,内 外导体表面的电场无切向分量,只有电场的径向分量。利用高斯定理和安培环路定理,容易求得 内外导体之间的电场和磁场分别为 , ln( ) U E e b a = 2π I H e = ( ) a b 内外导体之间任意横截面上的坡印廷矢量 同轴线中的电场、磁场和坡印廷矢量 (理想导体情况) S Ε H = H S 能流密度矢量 E O

UJ×(,2mp 5-ExH=le,pln(bla)" )=.2pin6la UI 电磁能量在内外导体之间的介质中沿轴方向流动,即由电源流向负载,如图所示。 Z 同轴线 穿过任意横截面的功率为: P=S.z.ds-p mn(bla) U πpdp=UI (2)当导体的电导率。为有限值时,导体内部存在沿电流方向的电场 E内 -e.nao 根据边界条件,在内导体表面上电场的切向分 因此,在内导体表 面乡 I H-6 2nd 同轴线中的电场、磁场和坡印廷矢量 (非理想体博 磁场则仍为 内导体表面外侧的坡印廷矢量为 2 UI (nx-d'a+e 2md mbla) 由此可见,内导体表面外侧的坡印廷矢量既有轴向分量,也有径向分量,如图所示。进入每单位 长度内导体的功率为 P=les-in2at- =RI 式中R=。是单位长度肉导体的电阻。由此可见,进入内导体中功率等于这段导
6 2 [ ] ( ) ln( ) 2π 2π ln( ) z U I UI S E H e e e b a b a = = = 电磁能量在内外导体之间的介质中沿轴方向流动,即由电源流向负载,如图所示。 穿过任意横截面的功率为: 2 d 2π d 2π ln( ) b z S a UI P S e S UI b a = = = (2)当导体的电导率σ为有限值时,导体内部存在沿电流方向的电场 根据边界条件,在内导体表面上电场的切向分量连续,即 → → = Z E外Z E内 因此,在内导体表 面外侧的电场为 2 ln( ) π z a U I E e e a b a a = 外 = + 磁场则仍为 内导体表面外侧的坡印廷矢量为 2 2 3 2 ( ) 2π 2π ln( ) z a a I UI S E H e e a a b a = = 外 外 外 = = − + 由此可见,内导体表面外侧的坡印廷矢量既有轴向分量,也有径向分量,如图所示。进入每单位 长度内导体的功率为 2 2 1 2 2 3 2 0 ( )d 2π d S a 2π π I I P S S a z RI a a = = − = = = 外 e 式中 2 1 a R = 是单位长度内导体的电阻。由此可见,进入内导体中功率等于这段导 内 2 π z J I E e a = = 同轴线 a 2π I H e a = 外 = 同轴线中的电场、磁场和坡印廷矢量 (非理想导体情况)

体的焦耳损耗功率」 以上分析表明电磁能量是由电磁场传输的,导体仅起着定向引导电磁能流的作用。当导 体的电导率为有限值时,进入导体中的功率全部被导体所吸收,成为导体中的焦耳热损耗功 率。 4.4惟一性定理 1.惟一性问题 在分析有界区域的时变电磁场问题时,常常需要在给定的初始条件和边界条件下,求解麦克斯韦 方程。那么,在什么定解条件下,有界区域中的麦克斯韦方程的解才是惟一的呢?这就是麦克斯 韦方程的解的惟一问题。 2.惟一性定理的表述 在以闭曲面S为边界的有界区域V内,如果给定t=0时刻的电场强度和磁场强度的初始值,并 且在t0时,给定边界面S上的电场强度的切向分量或磁场强度的切向分量,那么,在t>0时, 区域V内的电磁场由麦克斯韦方程惟一地确定。 3.惟一性定理的证明 利用反证法对惟一性定理给予证明。假设区域内的解不是惟一的,那么至少存在两组解E,、五, 和E,、H,满足同样的麦克斯韦方程,且具有相同的初始条件和边界条件。 令则在区域V内E。和H。的初始值为零:在边界面S上电场强度E。 的切向分量为零或 磁场强度H。的切向分量为零,且E。和H。满足麦克斯韦方程 Vx月,=a6+e6 x-u明 7.(uHo)=0 V.(E)=0 根据坡印廷定理,应有 -(Exdwr+LojEfar 根据E。和H。的边界条件,上式左端的被积函数为 (E×H)el=(尼×E)、=(i×E)E、=0 所以 +faEfdv-0 E。=E-E i。=i1-H2
7 体的焦耳损耗功率。 以上分析表明电磁能量是由电磁场传输的,导体仅起着定向引导电磁能流的作用。当导 体的电导率为有限值时,进入导体中的功率全部被导体所吸收,成为导体中的焦耳热损耗功 率。 4. 4 惟一性定理 1.惟一性问题 在分析有界区域的时变电磁场问题时,常常需要在给定的初始条件和边界条件下,求解麦克斯韦 方程。那么,在什么定解条件下,有界区域中的麦克斯韦方程的解才是惟一的呢?这就是麦克斯 韦方程的解的惟一问题。 2.惟一性定理的表述 在以闭曲面 S 为边界的有界区域 V 内,如果给定 t=0 时刻的电场强度和磁场强度的初始值,并 且在 t 0 时,给定边界面 S 上的电场强度的切向分量或磁场强度的切向分量,那么,在 t > 0 时, 区域 V 内的电磁场由麦克斯韦方程惟一地确定。 3.惟一性定理的证明 利用反证法对惟一性定理给予证明。假设区域内的解不是惟一的,那么至少存在两组解 → E1 、 → H1 和 → E2 、 → H2 满足同样的麦克斯韦方程,且具有相同的初始条件和边界条件。 令则在区域 V 内 → E0 和 → H0 的初始值为零;在边界面 S 上电场强度 → E0 的切向分量为零或 磁场强度 → H0 的切向分量为零,且 → E0 和 → H0 满足麦克斯韦方程 0 0 0 E H E t = + 0 0 H E t = − 0 = ( ) 0 H 0 = ( ) 0 E 根据坡印廷定理,应有 − = + + S V V H E V E V t E H e S )d d 2 1 2 1 ( d d ( ) d 2 0 2 0 2 0 0 n 0 根据 → E0 和 → H0 的边界条件,上式左端的被积函数为 0 0 n n 0 0 0 n 0 ( ) ( ) ( ) 0 S S S E H e e E H H e E = = = 所以 2 2 2 0 0 0 d 1 1 ( )d d 0 d 2 2 V V H E V E V t + + = E E E 0 1 2 = − H H H 0 1 2 = −

由于场的初始值为零,将上式两边对t积分,可得 5a。°+与eEw+E dv xur=0 上式中两项积分的被积函数均为非负的,要使得积分为零,必有 E。=0,i。=0即 E=E2,i1=H2 (证毕) 4.惟一性定理指出了获得惟一解所必须满足的条件,为电磁场问题的求解提供了理论依据,具 有非常重要的意义和广泛应用。 4.5时谐电磁场 讨论内容:时谐电磁场的复数表示:复矢量的麦克斯韦方程:复电容率和复磁导率:亥姆霍兹方 程:时谐场的位函数:平均能流密度矢量 4.5.1时谐电磁场的复数表示 1时谐电磁场的概念 如果场源以一定的角频率随时间呈时谐(正弦或余弦)变化,则所产生电磁场也以同样的角频率 随时间呈时谐变化。这种以一定角频率作时谐变化的电磁场,称为时谐电磁场或正弦电磁场。 2.研究时谐电磁场具有重要意义 在工程上,应用最多的就是时谐电磁场。广播、电视和通信的载波等都是时谐电磁场。 任意的时变场在一定的条件下可通过傅里叶分析方法展开为不同频率的时谐场的叠加。 3.时谐电磁场的复数表示 时谐电磁场可用复数方法来表示,使得大多数时谐电磁场问题的分析得以简化。 设A(?,)是一个以角频率随时间t作正弦变化的场量,它可以是电场和磁场的任意一个分 量,也可以是电荷或电流等变量,它与时间的关系可以表示成 A(行,t)=A,cos[ot+(F)】 实数表示法或瞬时表示法 式中的A0为振幅、分为与坐标有关的相位因子。 利用三角公式 4(F,t)=Reelo(r=Rel(F)ei] 其中 A()=A,e 照此法,矢量场的各分量Ei(i表示x、y或z)可表示成
8 由于场的初始值为零,将上式两边对 t 积分,可得 2 2 2 0 0 0 0 1 1 ( )d ( d )d 0 2 2 t V V H E V E V t + + = 上式中两项积分的被积函数均为非负的,要使得积分为零,必有 0 E = 0, 0 H = 0 即 1 2 E E = , H H 1 2 = (证毕) 4.惟一性定理指出了获得惟一解所必须满足的条件,为电磁场 问题的求解提供了理论依据,具 有非常重要的意义和广泛应用。 4. 5 时谐电磁场 讨论内容:时谐电磁场的复数表示;复矢量的麦克斯韦方程;复电容率和复磁导率;亥姆霍兹方 程;时谐场的位函数;平均能流密度矢量 4.5.1 时谐电磁场的复数表示 1.时谐电磁场的概念 如果场源以一定的角频率随时间呈时谐(正弦或余弦)变化,则所产生电磁场也以同样的角频率 随时间呈时谐变化。这种以一定角频率作时谐变化的电磁场,称为时谐电磁场或正弦电磁场。 2.研究时谐电磁场具有重要意义 在工程上,应用最多的就是时谐电磁场。广播、电视和通信的载波等都是时谐电磁场。 任意的时变场在一定的条件下可通过傅里叶分析方法展开为不同频率的时谐场的叠加。 3.时谐电磁场的复数表示 时谐电磁场可用复数方法来表示,使得大多数时谐电磁场问题的分析得以简化。 设 A(r,t) → 是一个以角频率 随时间 t 作正弦变化的场量,它可以是电场和磁场的任意一个分 量,也可以是电荷或电流等变量,它与时间的关系可以表示成 0 A r t A t r ( , ) cos[ ( )] = + 式中的 A0 为振幅、 → r 为与坐标有关的相位因子。 利用三角公式 j[ ( )] j 0 ( , ) Re e Re[ ( )e ] t r t A r t A A r + = = 其中 j ( ) 0 ( ) e r A r A = 照此法,矢量场的各分量 Ei(i 表示 x、y 或 z)可表示成 实数表示法或瞬时表示法 瞬时表示法

E(F.t)=Re[E(F)eJ-ReEelw4) 各分量合成以后,电场强度为 E(F,t)=Re[E (F)ei"] E(F)=eEm(F)(+Em()e(+(F)e() 4.有关复数表示的进一步说明 a.复数式只是数学表示方式,不代表真实的场。 b.真实场是复数式的实部,即瞬时表达式。 c.由于时间因子是默认的,有时它不用写出来,只用与坐标有关的部分就可表示复矢量。 例4.5.1将下列场矢量的瞬时值形式写为复数形式 (1) E(=,t)=@,Em cos(ot-k+)+Em sin(ot-k+) i(x,二,)=e,Hnk(巴)sin()sin(e-ot) +.H cos()cos(k-ot) (2) 解:(1)由于 武:,)=Ecos((o1-e+,)+e,Eco(@l-+4- =Rele,EE] 所以 E(e)=元,Ece-t+e,Ee-t2 =(e,Emeije (2)因为 cos(kz-@t)=cos(ot-kz) sin(-af)cos(co) 9
9 j j[ ( )] m ( , ) Re[ ( )e ] Re e i t t r E r t E r E i i i + = = 各分量合成以后,电场强度为 j m ( , ) Re[ ( )e ]t E r t E r = j ( ) j ( ) j ( ) m m m m ( ) ( )e ( )e ( )e x y z r r r E r e E r e E r e E r x x y y z z = + + 4.有关复数表示的进一步说明 a. 复数式只是数学表示方式,不代表真实的场。 b. 真实场是复数式的实部,即瞬时表达式。 c. 由于时间因子是默认的,有时它不用写出来,只用与坐标有关的部分就可表示复矢量。 例 4.5.1 将下列场矢量的瞬时值形式写为复数形式 (1) m m ( , ) cos( ) sin( ) E z t e E t kz e E t kz = − + + − + x x x y y y (2) m m π ( , , ) ( )sin( )sin( ) π π cos( )cos( ) x z a x H x z t e H k kz t a x e H kz t a = − + − 解:(1)由于 m m π ( , ) cos( ) cos( ) 2 E z t e E t kz e E t kz = − + + − + − x x x y y y j( ) j( π/ 2) Re[ e e ] m m x y t kz t kz x x y y e E e E − + − + − = + 所以 j( ) j( π/ 2) m m m ( ) e e x y kz kz E z e E e E x x y y − + − + − = + j j j m m ( e j e )e x y kz x x y y e E e E − = − (2)因为 cos( ) cos( ) kz t t kz − = − π π sin( ) cos( ) cos( ) 2 2 kz t kz t t kz − = − − = − +

所以 月x,z,)=a,Hnk()sin)sin(ke-or)+ .H cos()cos(k-ot) -g,H_k()sin()cos(t-k+)+ .cosco() i(x,)=E,H.k马)sin(西ek+即+E.Hcos(ek 例4.5.2已知电场强度复矢量 E(=)=@jEm cos(k.=) 其中kz和Exm为实常数。写出电场强度的瞬时矢量 解: E(=,t)=Rel@,jEm cos(k.)ei] =Rele,Ecos(k.=)e co()cos(o+) =-e,E,m cos(k.z)sin(@t) 4.5.2复矢量的麦克斯韦方程 以电场旋度方程 xE为要代入相应场量的矢量,可得 V×Re(Ee】=-Re(ae】 将,会与Re交换次序, Revx(店.e月=-Re号(a.eI=Re-joi.e] 10
10 所以 m m π ( , , ) ( )sin( )sin( ) π π cos( )cos( ) x z a x H x z t e H k kz t a x e H kz t a = − + − m m π π ( )sin( )cos( ) π 2 π cos( )cos( ) x z a x e H k t kz a x e H t kz a = − + + − 故 j jπ 2 j m m m π π ( , ) ( )sin( )e cos( )e π kz kz x z a x x H x z e H k e H a a − + − = + 例 4.5.2 已知电场强度复矢量 m m ( ) j cos( ) E z e E k z = x x z 其中 kz 和 Exm 为实常数。写出电场强度的瞬时矢量 解: j m π j( ) 2 m ( , ) Re[ j cos( )e ] Re[ cos( )e ] t x x z t x x z E z t e E k z e E k z + = = m π cos( )cos( ) 2 x x z = + e E k z t m cos( )sin( ) x x z = −e E k z t 4.5.2 复矢量的麦克斯韦方程 以电场旋度方程 为例,代入相应场量的矢量,可得 j j m m [Re( e )] [Re( e )] t t E B t = − 将 、 t 与 Re 交换次序,得 j j j Re[ ( e )] Re[ ( e )] Re[ j e ] m m m t t t E B B t = − = − t B E = −