《电磁场理论》课程电子教案（讲义）第二章 电磁场的基本规律

第2章电磁场的基本规律 本章讨论内容 2.1 电荷守恒定律 2.2 真空中静电场的基本规律 2.3 真空中恒定磁场的基本规律 电荷 电流 2.4 媒质的电磁特性 (运动) 2.5 电磁感应定律和位移电流 磁场 2.6 麦克斯韦方程组 电场 2.7 电磁场的边界条件 2.1电荷守恒定律 电磁场物理模型中的基本物理量可分为源量和场量两大类。 源量为电荷9，)和电流行，)，分别用来描述产生电磁效应的两类场源。电荷是产生 电场的源，电流是产生磁场的源。 本节内容 2.1.1电荷与电荷密度 2.1.2电流与电流密度 2.1.3电荷守恒定律 2.1.1电荷与电荷密度 ·电荷是物质基本属性之一 ·1897年英国科学家汤姆进(JJ.Thomson)在实验中发现了电子。 ·1907一1913年间，美国科学家密立根(R.A.Milike)通过油滴实验，精确测定电子电荷的 量值为e=1.60217733×10-19(单位：C)确认了电荷的量子化概念。换句话说，e是最小的 电荷，而任何带电粒子所带电荷都是e的整数倍。 ·宏观分析时，电荷常是数以亿计的电子电荷©的集合，故可不考虑其量子化的事实，而认 为电荷1量g可任意连续取值。 理想化实际带电系统的电荷分布形态分为四种形式：点电荷、体分布电荷、面分布电荷、 线分布电荷 1.电荷体密度 电荷连续分布于体积V内，用电荷体密度来描述其分布 Aq(F)=da(F) p=m。A7 单位：Cm3(库/米3) 根据电荷密度的定义，如果已知某空间区域V中的电荷体密度，则区域V中的总电荷q 为

1 第2章 电磁场的基本规律 本章讨论内容 2.1 电荷守恒定律 2.2 真空中静电场的基本规律 2.3 真空中恒定磁场的基本规律 2.4 媒质的电磁特性 2.5 电磁感应定律和位移电流 2.6 麦克斯韦方程组 2.7 电磁场的边界条件 2.1 电荷守恒定律 电磁场物理模型中的基本物理量可分为源量和场量两大类。 源量为电荷 q(r  ,t)  和电流 I(r  ,t)  ，分别用来描述产生电磁效应的两类场源。电荷是产生 电场的源，电流是产生磁场的源。 本节内容 2.1.1 电荷与电荷密度 2.1.2 电流与电流密度 2.1.3 电荷守恒定律 2.1.1 电荷与电荷密度 • 电荷是物质基本属性之一。 • 1897 年英国科学家汤姆逊(J.J.Thomson)在实验中发现了电子。 • 1907 — 1913 年间，美国科学家密立根(R.A.Miliken)通过油滴实验，精确测定电子电荷的 量值为 e =1.602 177 33×10-19 (单位：C ) 确认了电荷的量子化概念。换句话说，e 是最小的 电荷，而任何带电粒子所带电荷都是 e 的整数倍。 • 宏观分析时，电荷常是数以亿计的电子电荷 e 的集合，故可不考虑其量子化的事实，而认 为电荷 1 量 q 可任意连续取值。 理想化实际带电系统的电荷分布形态分为四种形式：点电荷、体分布电荷、面分布电荷、 线分布电荷 1. 电荷体密度 电荷连续分布于体积 V 内，用电荷体密度来描述其分布 V q r V q r r V d d ( ) Δ Δ ( ) ( ) lim Δ 0    = = →  单位：C/m3 (库/米 3 ) 根据电荷密度的定义，如果已知某空间区域 V 中的电荷体密度，则区域 V 中的总电荷 q 为 电荷 电流 电场 磁场 （运动） q V y x z o r V

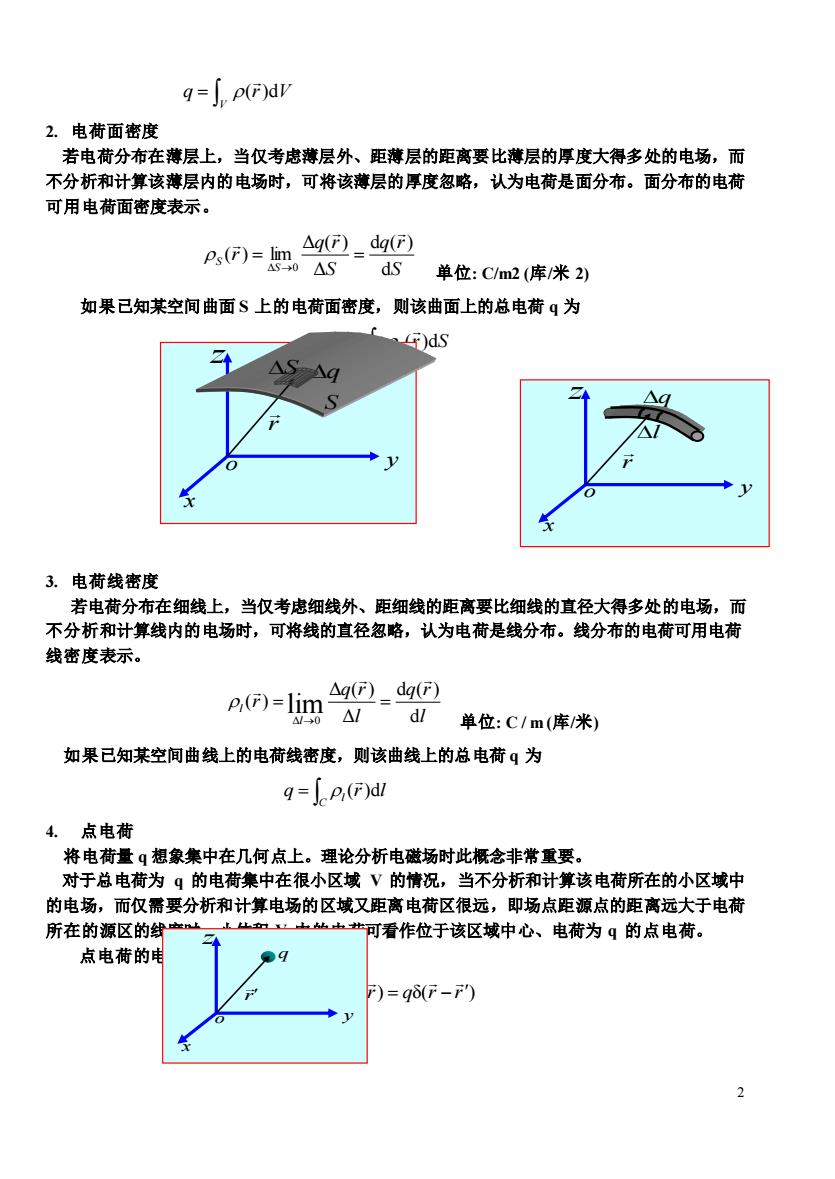
q=f p(F)dv 2.电荷面密度 若电荷分布在薄层上，当仅考虑薄层外、距薄层的距离要比薄层的厚度大得多处的电场，而 不分析和计算该薄层内的电场时，可将该薄层的厚度忽略，认为电荷是面分布。面分布的电荷 可用电荷面密度表示。 同-如智.智单c南米 如果已知某空间曲面S上的电荷面密度，则该曲面上的总电荷q为 ds △S 3.电荷线密度 若电荷分布在细线上，当仅考虑细线外、距细线的距离要比细线的直径大得多处的电场，而 不分析和计算线内的电场时，可将线的直径忽略，认为电荷是线分布。线分布的电荷可用电荷 线密度表示。 △q()_dq(F) P,=lm=d山单位：C1m(库米) 如果已知某空间曲线上的电荷线密度，则该曲线上的总电荷q为 q=[p(F)dl 4.点电荷 将电荷量q想象集中在几何点上。理论分析电磁场时此概念非常重要。 对于总电荷为q的电荷集中在很小区域V的情况，当不分析和计算该电荷所在的小区域中 的电场，而仅需要分析和计算电场的区域又距离电荷区很远，即场点距源点的距离远大于电荷 所在的源区的线 ”可看作位于该区域中心、电荷为q的点电荷。 点电荷的 F)=g(F-F)

2  = V q (r)dV   2. 电荷面密度 若电荷分布在薄层上，当仅考虑薄层外、距薄层的距离要比薄层的厚度大得多处的电场，而 不分析和计算该薄层内的电场时，可将该薄层的厚度忽略，认为电荷是面分布。面分布的电荷 可用电荷面密度表示。 S q r S q r r S S d d ( ) Δ Δ ( ) ( ) lim Δ 0    = = →  单位: C/m2 (库/米 2) 如果已知某空间曲面 S 上的电荷面密度，则该曲面上的总电荷 q 为  = S q s (r)dS   3. 电荷线密度 若电荷分布在细线上，当仅考虑细线外、距细线的距离要比细线的直径大得多处的电场，而 不分析和计算线内的电场时，可将线的直径忽略，认为电荷是线分布。线分布的电荷可用电荷 线密度表示。 l q r l q r r l l d d ( ) Δ Δ ( ) ( ) lim Δ 0    = = →  单位: C / m (库/米) 如果已知某空间曲线上的电荷线密度，则该曲线上的总电荷 q 为  = C l q (r)dl   4. 点电荷 将电荷量 q 想象集中在几何点上。理论分析电磁场时此概念非常重要。 对于总电荷为 q 的电荷集中在很小区域 V 的情况，当不分析和计算该电荷所在的小区域中 的电场，而仅需要分析和计算电场的区域又距离电荷区很远，即场点距源点的距离远大于电荷 所在的源区的线度时，小体积 V 中的电荷可看作位于该区域中心、电荷为 q 的点电荷。 点电荷的电荷密度表示 (r) = qδ(r − r )     y x z o r S q S y x z o r q l y x z o r  q

2.1.2电流与电流密度 电流 电荷的定向运动而形成，用1表示，其大小定义为：单位时间内通过某一横 装面s的电荷量，即=（公）=% 单位：A(安) 电流方向：正电荷的流动方向 形成电流的条件： （1)存在可以自由移动的电荷； （2)存在电场。 说明：电流通常是时间的函数，不随时间变化的电流称为恒定电流，用表示。 一般情况下，在空间不同的点，电流的大小和方向往往是不同的。在电磁理论中，常用体电 流、面电流和线电流来描述电流的分别状态。 1.体电流 电荷在某一体积内定向运动所形成的电流称为体电流，用电流密度矢量J」来描述。 单位：A/m2(安/米2) }正电荷运动的方向 i=[J.ds 流过任意曲面S的电流为 2.面电流 电荷在一个厚度可以忽略的薄层内定向运动所形成的电流称为面电流，用面电流密度矢量 J5来描述其分布 片正电荷运动的方向 .Ai di Js-eMoN-6d 单位：/m(安/米)。 e 通透鑫春经富鑫六的电流我时有 显见有角度因素存在即： C效的宽 △l=Jsl1=JsAl-sina ○ 其中a为j与△I的夹角。 -dl dl 由于：sina=nsin a=n(i×j)故有： △1=[（△）×(Js)]=(A7×J) 2.2.10

3 此时有 效的宽 度 2.1.2 电流与电流密度 电流 —— 电荷的定向运动而形成，用 i 表示，其大小定义为： 单位时间内通过某一横 截面 S 的电荷量，即 dt dq t q i t =   =  → lim ( ) 0 单位: A （安） 电流方向: 正电荷的流动方向 形成电流的条件： （1）存在可以自由移动的电荷; （2）存在电场。 说明：电流通常是时间的函数，不随时间变化的电流称为恒定电流，用 I 表示。 一般情况下，在空间不同的点，电流的大小和方向往往是不同的。在电磁理论中，常用体电 流、面电流和线电流来描述电流的分别状态。 1. 体电流 电荷在某一体积内定向运动所形成的电流称为体电流，用电流密度矢量 J  来描述。 dS di e S i J e n s n    =   =  →0 lim 单位：A / m2 （安/米 2） 。 流过任意曲面 S 的电流为 i J S S   = d  2. 面电流 电荷在一个厚度可以忽略的薄层内定向运动所形成的电流称为面电流，用面电流密度矢量 S J  来描述其分布 dl di e l i J e t l S t    =   =  →0 lim 单位：A/m （安/米） 。 通过薄导体层上任意有向曲线 的电流为 ( d ) n i J e l l S    =    正电荷运动的方向 正电荷运动的方向 sin S S I J l J l  J l  =  ⊥ =     显见有 因素存在即： 其中 为 与 的夹 。 角度 角 任意表面 元Δl表面 流： ( ) ( ) ( ) sin sin ( ) S 2.2.10 n n n l j I n l l jJ n l J   = =   =   =       由于： 故有：

例题2.2.2表面电流J=(exy+eyx)AWm计算空间(2,1)及(5，l)间的线段电流。 由力线方程：dF×F)=0或 斋斋斋和 ddyx-y=ki V x 显然：di=e(y恒定，仅沿x移动) 法线方向n=E,于是： 1=je,y+e,r小民×e,)=xd=l0.5m4 循环不变：正序取正 差乘法则E,6,ee6,e 逆序取负 线电流及电流的类型 线电流：电荷在一根很细的导线中流动导线的截面积很小时的电流。 近似认为是无限细：I=P,·下 电流是由电荷运动产生的。 根据载体的不同可分为：体电流」在体积元中 面电流Js-在表面元中 线电流J-在线元中 运动的驱动力：来源于外界的各种源如 机械能、热能、化学能、光能、电磁能（感应） 2.1.3电荷守恒定律（电流连续性方程) 电荷守恒定律：电荷既不能被创造，也不能被消灭，只能从物体的一部分转移到另一部分， 或者从一个物体转移到另一个物体。 电荷守恒定律是电磁现象中的基本定律之一。 电流连续性方程 流出闭曲面S的电流等于 体积V内单位时间所减少 :的电荷量 任意有向曲线穿过的电流： 微分形f-×@网=∫Js(n×d） 恒定电流是无源场，电流线】 是连续的闭合曲线，既无起 点也无终点 4

4 例题 2.2.2 表面电流 J=(exy+ eyx)A/m,计算空间（2,1）及(5,1)间的线段电流。 2 2 2 ( ) ( ) ( ) ( ) 0; x y K x dy y dx F r dz F r dy F r dx dr F r x y z =  − = = =   有： 由力线方程： 或       I (e y e x) (e e dx) xdx mA n e dl e dx y l x y z x z x 10.5 , x 0.05 0.02 = + •  = = = =            法线方向 于是： 显然： （ 恒定，仅沿 移动） 循环不变：正序取正 , , , , , , x y z x y z e e e e e e       差乘法则 逆序取负 线电流及电流的类型 线电流：电荷在一根很细的导线中流动导线的截面积很小时的电流。 I v l  近似认为是无限细： =   电流是由电荷运动产生的。 根据载体的不同可分为：体电流 J -在体积元中 面电流 Js -在表面元中 线电流 Jl -在线元中 运动的驱动力：来源于外界的各种源如 机械能、热能、化学能、光能、电磁能（感应） 2.1.3 电荷守恒定律（电流连续性方程） 电荷守恒定律:电荷既不能被创造，也不能被消灭，只能从物体的一部分转移到另一部分， 或者从一个物体转移到另一个物体。 电荷守恒定律是电磁现象中的基本定律之一。 电流连续性方程 积分形式：    = − = − S V V t t q J S d d d d d d    微分形式： t J    = −   ( S S ) ( ) 2.2.11 l l I n dl J J n dl =  =    任意有向曲线穿过的电流： 流出闭曲面 S 的电流等于 体积 V 内单位时间所减少 的电荷量 恒定电流是无源场，电流线 是连续的闭合曲线，既无起 点也无终点

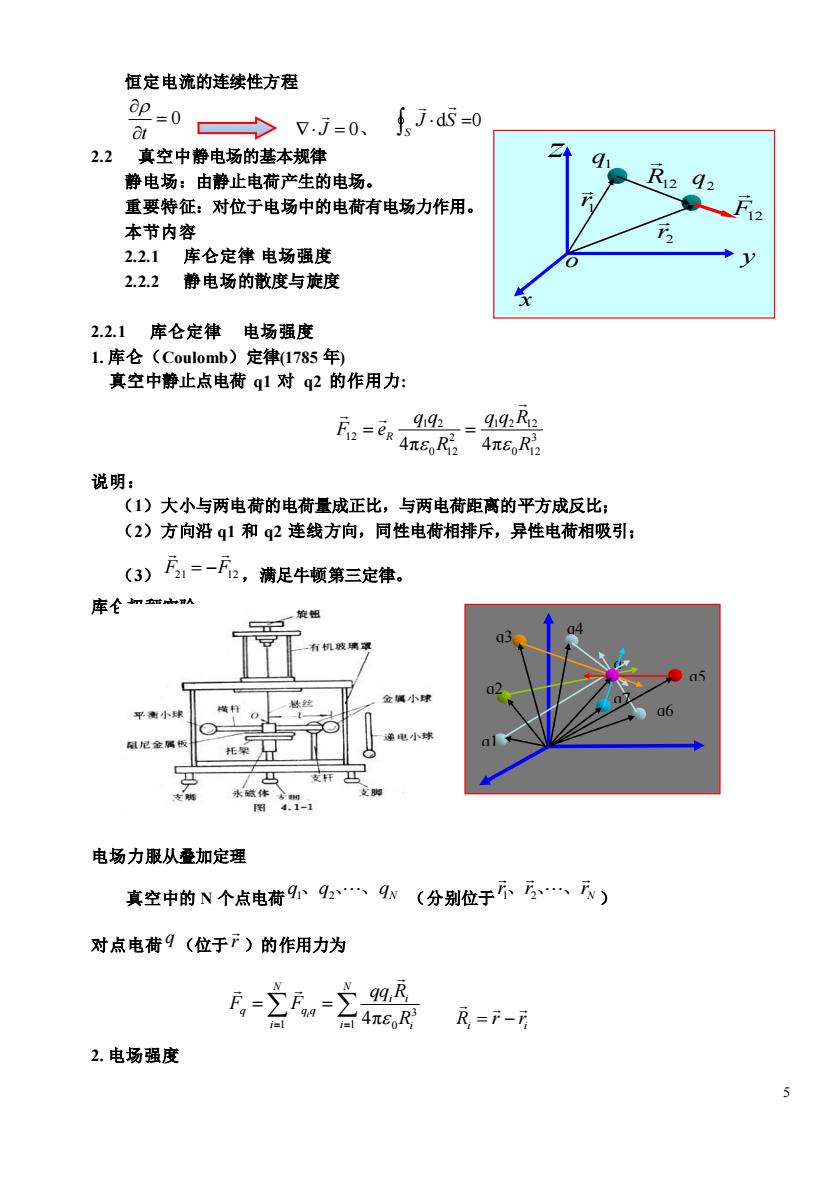
恒定电流的连续性方程 -0>7-0. fJ.ds=0 2.2真空中静电场的基本规律 静电场：由静止电荷产生的电场。 重要特征：对位于电场中的电荷有电场力作用 F 本节内容 2.2.1库仑定律电场强度 2.2.2静电场的散度与旋度 2.2.1库仑定律电场强度 1.库仑(Coulomb)定律(1785年) 真空中静止点电荷q1对q2的作用力： 店器是 说明： (1)大小与两电荷的电荷量成正比，与两电荷距离的平方成反比 (2)方向沿q1和q2连线方向，同性电荷相排斥，异性电荷相吸引： (3)1=-F2,满足牛顿第三定律。 库仑如人 细 平小 尼金属 电场力服从叠加定理 真空中的N个点电荷、9w(分别位于不.、) 对点电荷q(位于F)的作用力为 台4πR 反=F- 2.电场强度

5 恒定电流的连续性方程 = 0   t   J = 0、  d 0   = S J S   2.2 真空中静电场的基本规律 静电场：由静止电荷产生的电场。 重要特征：对位于电场中的电荷有电场力作用。 本节内容 2.2.1 库仑定律 电场强度 2.2.2 静电场的散度与旋度 2.2.1 库仑定律 电场强度 1. 库仑（Coulomb）定律(1785 年) 真空中静止点电荷 q1 对 q2 的作用力: 3 0 12 1 2 12 2 0 12 1 2 12 4π 4π R q q R R q q F eR      = = 说明： （1）大小与两电荷的电荷量成正比，与两电荷距离的平方成反比； （2）方向沿 q1 和 q2 连线方向，同性电荷相排斥，异性电荷相吸引； （3） F21 F12   = − ，满足牛顿第三定律。 库仑扭秤实验 电场力服从叠加定理 真空中的 N 个点电荷 q1、q2、、qN （分别位于 N r r r     1、 2、 、 ） 对点电荷 q （位于 r  ）的作用力为   = = = = N i i i i N i q q q R qq R F F i 1 3 1 4π 0     i i R r r    = − 2. 电场强度 y x z o 1 r q1 2 r R12 F12 q2 q q1 q2 q3 q4 q5 q6 q7

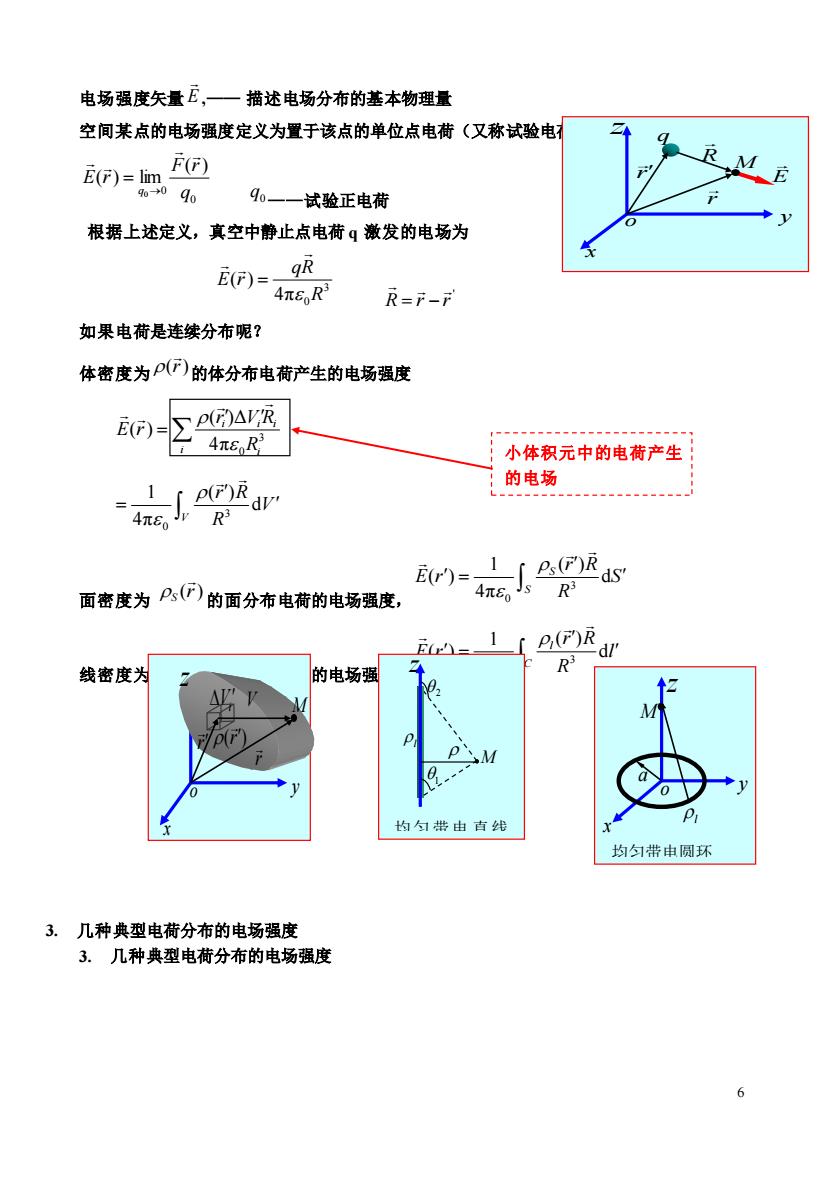
电场强度矢量E,一描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷（又称试验电 前婴 M 90一一试验正电荷 根据上述定义，真空中静止点电荷q激发的电场为 gR E0)=4G,R R=F-r 如果电荷是连续分布呢？ 体密度为P)的体分布电荷产生的电场强度 E)=∑py见 4π8R 小体积元中的电荷产生 的电场 -dV R3 面密度为P,的面分布电荷的电场强度， E(r)=)s R E= 线密度为 的电场强 均匀带由直线 均匀带电圆环 3.几种典型电荷分布的电场强度 3.几种典型电荷分布的电场强度 6

6 电场强度矢量 E  ,—— 描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷（又称试验电荷）受到的作用力，即 0 0 ( ) ( ) lim 0 q F r E r q     → = 0 q ——试验正电荷 根据上述定义，真空中静止点电荷 q 激发的电场为 3 4π 0 ( ) R qR E r     = ' R r r    = − 如果电荷是连续分布呢？ 体密度为 (r)   的体分布电荷产生的电场强度    = i i i i i R r V R E r 3 4π 0 ( )Δ ( )          = V V R r R d ( ) 4π 1 3 0     面密度为 (r) S   的面分布电荷的电场强度，     = S S S R r R E r d ( ) 4π 1 ( ) 3 0      线密度为 (r) S   的线分布电荷的电场强度，     = C l l R r R E r d ( ) 4π 1 ( ) 3 0      3. 几种典型电荷分布的电场强度 3. 几种典型电荷分布的电场强度 y x z o r  q r R E M 小体积元中的电荷产生 的电场 ( ) r  V y x z o r  Vi   r M l 1   z M 2  均匀带电 直线 段 l y x z o M a 均匀带电圆环

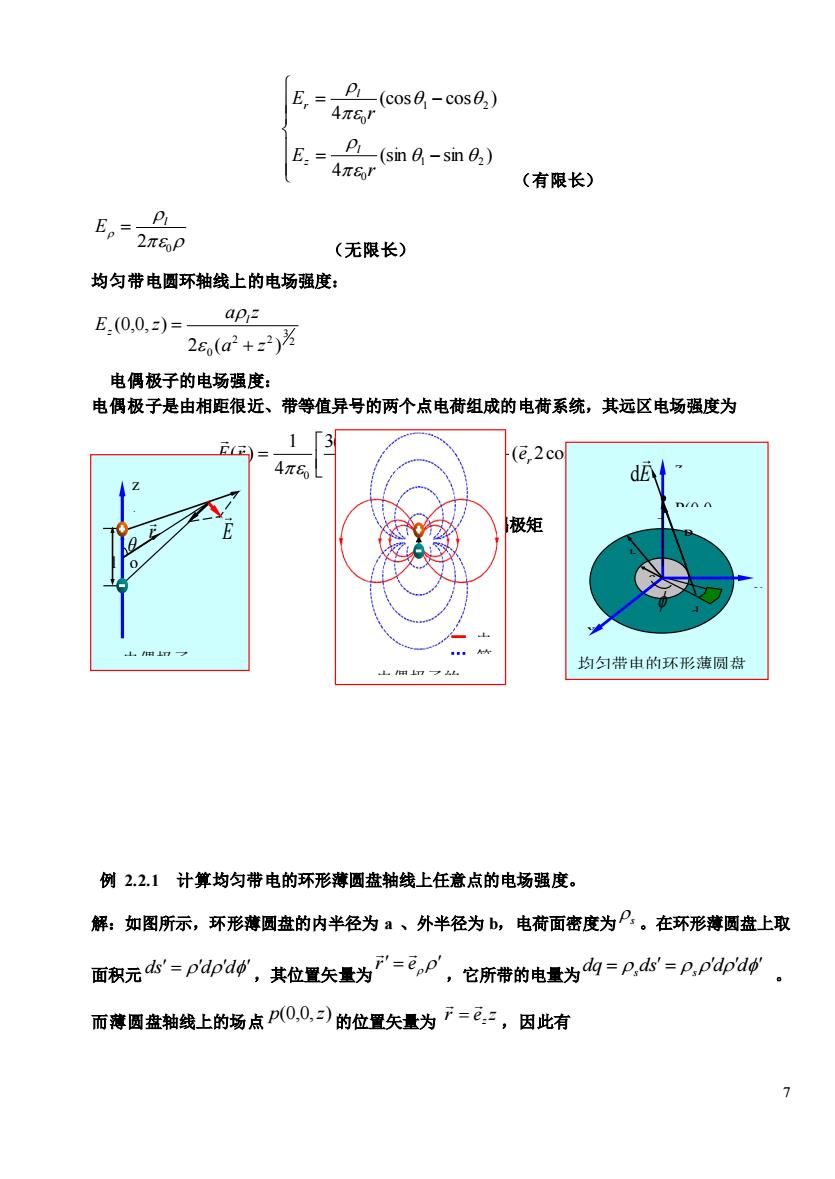
P(cos0,-cos0;) E,4 P(sin 0-sin 0;) E4r (有限长) E,2 (无限长) 均匀带电圆环轴线上的电场强度： E.(0,0,)= ap 2c(a2+z23 电偶极子的电场强度： 电偶极子是由相距很近、带等值异号的两个点电荷组成的电荷系统，其远区电场强度为 1 3 (e.2co π6 极矩 均匀带由的环形薄圆盘 例221计算均匀带电的环形薄圆盘轴线上任意点的电场强度。 解：如图所示，环形薄圆盘的内半径为a、外半径为b,电荷面密度为P。在环形薄圆盘上取 面积元dk=ppa0,其位置矢量为'=e,D,它所带的电量为d内=p,本=.dp 而薄圆盘轴线上的场点P0,0,)的位置矢量为F=:,因此有

7        = − = − (sin sin ) 4 (cos cos ) 4 1 2 0 1 2 0           r E r E l z l r （有限长）     2 0 l E = （无限长） 均匀带电圆环轴线上的电场强度： 2 3 2 2 0 2 ( ) (0,0, ) a z a z E z l z + =   电偶极子的电场强度： 电偶极子是由相距很近、带等值异号的两个点电荷组成的电荷系统，其远区电场强度为 ( 2cos sin ) 4 3( ) 4 1 ( ) 3 0 5 3 0        e e r p r p r p r r E r r         = +       −  = p ql   = ——电偶极矩 例 2.2.1 计算均匀带电的环形薄圆盘轴线上任意点的电场强度。 解：如图所示，环形薄圆盘的内半径为 a 、外半径为 b，电荷面密度为 s 。在环形薄圆盘上取 面积元 ds  = dd ，其位置矢量为 r  = e   ，它所带的电量为 dq =  ds  =  dd s s 。 而薄圆盘轴线上的场点 p(0,0,z) 的位置矢量为 r e zz   = ，因此有  r E + q 电偶极子 z l o － q 电偶极子的 场图 等 位 线 电 场 线 P(0,0, z) b r R y z x 均匀带电的环形薄圆盘 d S  a dE

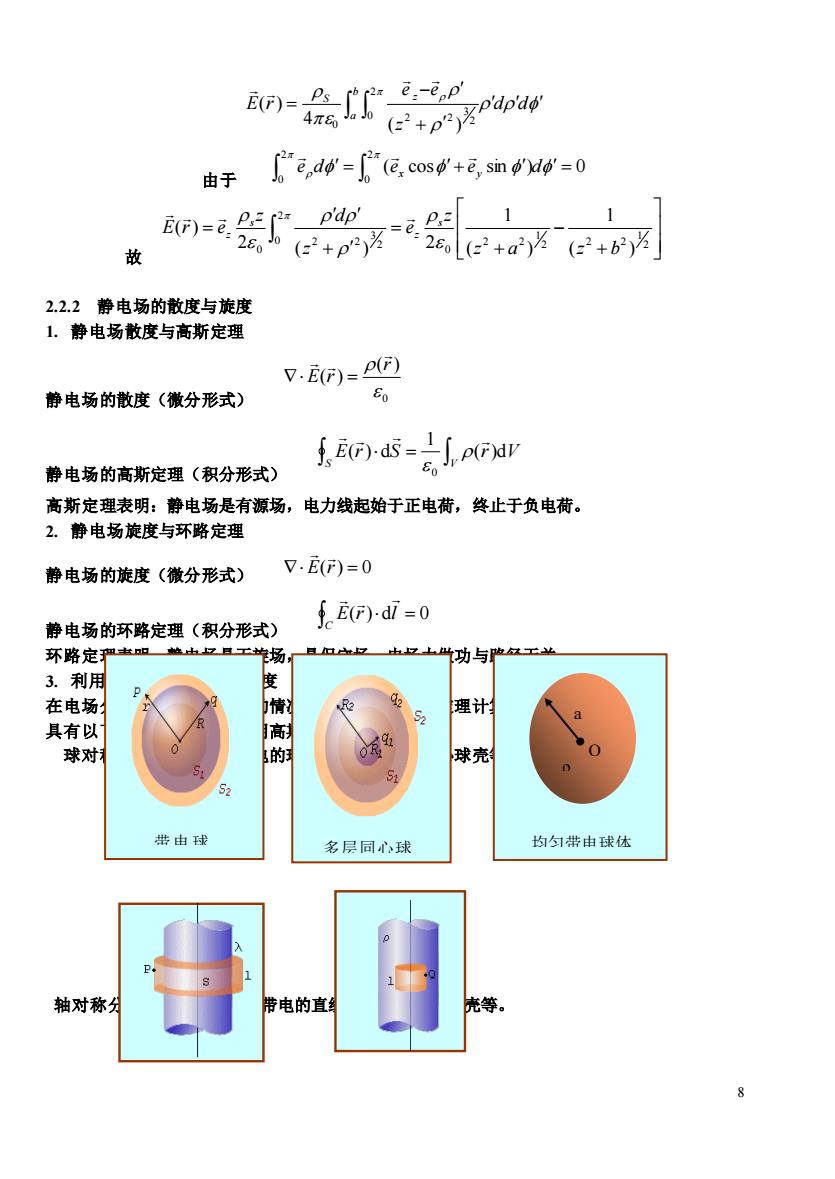
n-afraww 由于 do"(cos,si 1 年 、=62+03=g1 F2e2+a27(e2+6」 2.2.2静电场的散度与旋度 1.静电场散度与高斯定理 .E)= 静电场的散度（徽分形式） 60 静电场的高斯定理（积分形式） 美，i5- 高斯定理表明：静电场是有源场，电力线起始于正电荷，终止于负电荷。 2.静电场旋度与环路定理 静电场的旋度（微分形式） V.E)=0 静电场的环路定理（积分形式） fE0)-d=0 环路定严 功与■ 3.利用 度 在电场 理计」 具有以 球对 的 球壳 带由 名层同球 均匀带由球休 轴对称 寺电的直

8              +  −  =   d d z e e E r b a S z 2 0 2 3 2 2 0 ( ) 4 ( )     由于 ( cos sin ) 0 2 0 2 0  =  +   =         ed ex ey d    故         + − + = +    =  2 1 2 2 2 1 2 2 0 2 0 2 3 2 2 0 ( ) 1 ( ) 1 2 ( ) 2 ( ) z a z b z e z z d E r e s z s z             2.2.2 静电场的散度与旋度 1. 静电场散度与高斯定理 静电场的散度（微分形式） 0 ( ) ( )   r E r     = 静电场的高斯定理（积分形式）    = S V E r S (r)dV 1 ( ) d 0       高斯定理表明：静电场是有源场，电力线起始于正电荷，终止于负电荷。 2. 静电场旋度与环路定理 静电场的旋度（微分形式） E(r) = 0   静电场的环路定理（积分形式） ( )d = 0 C E r l    环路定理表明：静电场是无旋场，是保守场，电场力做功与路径无关。 3. 利用高斯定理计算电场强度 在电场分布具有一定对称性的情况下，可以利用高斯定理计算电场强度。 具有以下几种对称性的场可用高斯定理求解： 球对称分布：包括均匀带电的球面，球体和多层同心球壳等。 轴对称分布：如无限长均匀带电的直线，圆柱面，圆柱壳等。 带电球 壳 多层同心球 壳 均匀带电球体 a O ρ 0

无限大平面电荷：如无限大的均匀带电平面、平板等。 例2.2.2求真空中均匀带电球体的场强分布。已知球体半径为a,电有 解：(1)球外某点的场强 由于 (2)求球体内一点的场强 由于 iEd-Ag→ 4rEa万r→E=0) 2.3真空中恒定磁场的基本规律 本节内容 2.31安培力定律磁感应强度 2.3.2恒定磁场的散度与旋度 2.3.1安培力定律磁感应强度 1.安培力定律 安培对电流的磁效应进行了大量的实验研究，在1821一1825年之间，设计并完成了电 流相互作用的精巧实验，得到了电流相互作用力公式，称为安培力定律， 实验表明，真空中的载流回路C1对载流回路C2的作用力 后会人xE 安培力定律 R 载流回路C2对载流回路C1的作用力1=-斤。 ←一满足牛顿第三定律 2.磁感应强度 电流在其周围空间中产生磁场，描述磁场分布的基本物理量是磁感应强度B,单位为T(特 斯拉)。 磁场的重要特征是对场中的电流磁场力作用，载流回路C1对载流回路C2的作用力是回 路C1中的电流Ⅱ产生的磁场对回路C2中的电流2的作用力。 根据安培力定律，有

9 无限大平面电荷：如无限大的均匀带电平面、平板等。 例 2.2.2 求真空中均匀带电球体的场强分布。已知球体半径为 a ，电 荷密度为 0 。 解：（1）球外某点的场强 由于 0 3 0 0 π 3 1 4 d    a q E S S  = =    ( r a ) 3 2 0 3 0 =  r a E   （2）求球体内一点的场强 由于 E S V S V  = d 1 d 0 0     3 3 0 2 π 3 4 4π 3 1 4 r a q r E =     ( ) 3 0 0 r a r E =    2.3 真空中恒定磁场的基本规律 本节内容 2.3.1 安培力定律 磁感应强度 2.3.2 恒定磁场的散度与旋度 2.3.1 安培力定律 磁感应强度 1. 安培力定律 安培对电流的磁效应进行了大量的实验研究，在 1821 —1825 年之间，设计并完成了电 流相互作用的精巧实验，得到了电流相互作用力公式，称为安培力定律。 实验表明，真空中的载流回路 C1 对载流回路 C2 的作用力     = 2 1 3 12 0 2 2 1 1 12 12 d ( d ) 4π C C R I l I l R F      载流回路 C2 对载流回路 C1 的作用力 F21 F12   = − 2. 磁感应强度 电流在其周围空间中产生磁场，描述磁场分布的基本物理量是磁感应强度 B  ，单位为 T（特 斯拉）。 磁场的重要特征是对场中的电流磁场力作用，载流回路 C1 对载流回路 C2 的作用力是回 路 C1 中的电流 I1 产生的磁场对回路 C2 中的电流 I2 的作用力。 根据安培力定律，有 a r 0 r r E a 安培力定律 满足牛顿第三定律

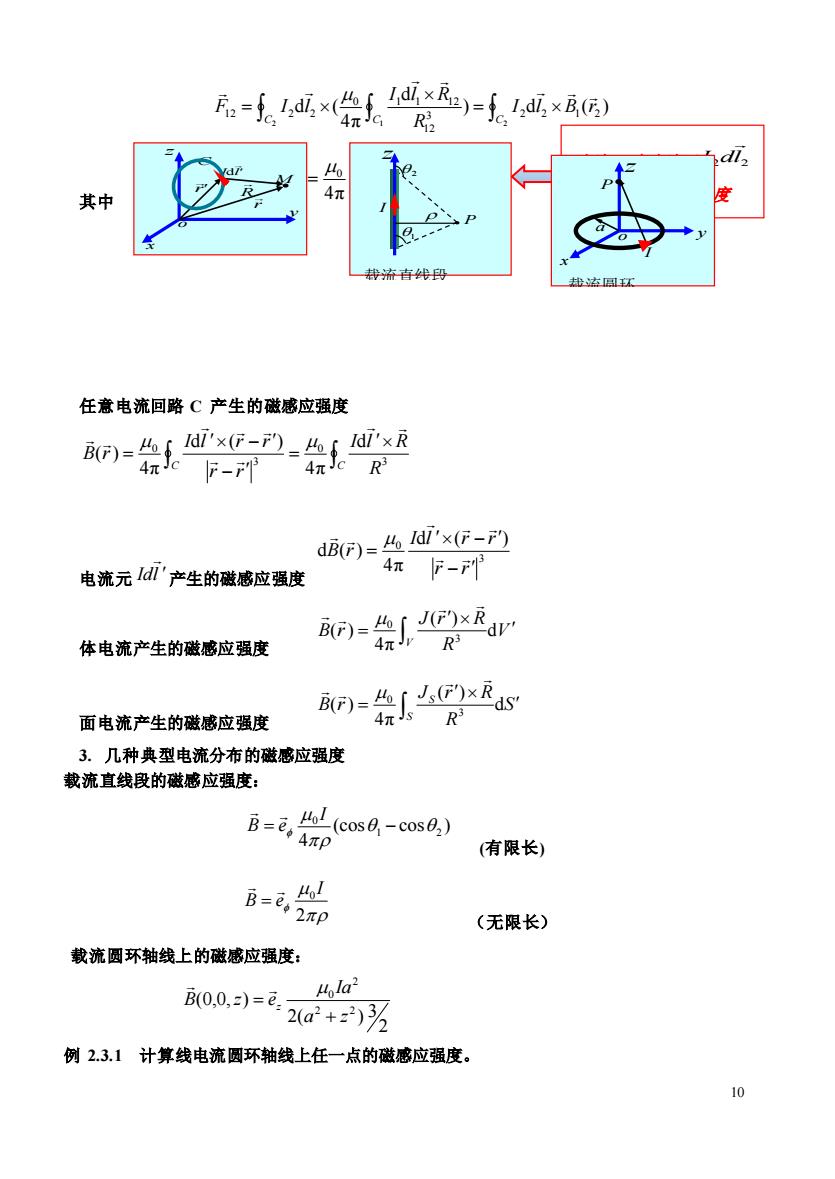
尼-.哈1，)-1感园 任意电流回路C产生的磁感应强度 n-会P-会10 C R d)='x(FF) 电流元I'产生的磁感应强度 4πF- 体电流产生的磁感应强度 i)av F)()xRas 面电流产生的磁感应强度 4πJ R 3.几种典型电流分布的磁感应强度 载流直线段的磁感应强度： (coco.) (有限长) Bn (无限长) 载流圆环轴线上的磁感应强度： ula2 0.0,）=0202+)% 例2.3.1计算线电流圆环轴线上任一点的磁感应强度。 10

10    =   =  2 1 2 ) d ( ) d 4π d ( 3 2 2 1 2 12 0 1 1 12 12 2 2 C C C I l B r R I l R F I l         其中   = 1 3 12 0 1 1 12 1 2 d 4π ( ) C R I l R B r      任意电流回路 C 产生的磁感应强度    = −   −  = C C R I l R r r I l r r B r 3 0 3 0 d 4π d ( ) 4π ( )            电流元 Idl   产生的磁感应强度 3 0 d ( ) 4π d ( ) r r I l r r B r −   −  =         体电流产生的磁感应强度 V R J r R B r V    =  d ( ) 4π ( ) 3 0      面电流产生的磁感应强度 S R J r R B r S S    =  d ( ) 4π ( ) 3 0      3. 几种典型电流分布的磁感应强度 载流直线段的磁感应强度： (cos cos ) 4 1 2 0      =  − I B e   (有限长)    2 0 I B e   = （无限长） 载流圆环轴线上的磁感应强度： 2 3 2( ) (0,0, ) 2 2 2 0 a z Ia B z ez + =    例 2.3.1 计算线电流圆环轴线上任一点的磁感应强度。 电流 I1在电流元 2 2 I dl  处产生的磁感应强度 y x z o r  Il d  r R C M I 1  z P  2 载流直线段 I y x z o P a 载流圆环