
第7章导行电磁波(不要随便修改格式,否则) 导行电磁波一一被限制在某一特定区域内传播的电磁波 导波系统一一引导电磁波从一处定向传输到另一处的装置 常用的导波系统的分类:TEM传输线、金属波导管、表面波导。 1.TEM波传输线 平行线 同轴波导 平行双导线是最简单的TEM波传输线,随着工作频率的升高,其辐射损耗急剧增加,故双 导线仅用于米波和分米波的低频段。 同轴线没有电磁辐射,工作频带很宽 2.波导管 矩形波 导 波导是用金属管制作的导波系统, 电磁波在管内传播,损耗很小, 主要用于3GHz ~30GHz的频 率范围。 本章内容 71 导行电磁波概论 矩形波导 7.3 圆柱形波导 7.4 同轴波导 75 谐振腔 7.6 传输线 7.1导行电磁波概论 分析均匀波导系统时,做如下假定: 波导是无限长的规则直波导,其横截面形状可以任意,但沿轴向处处相同,沿2轴方向放 1
1 第7章 导行电磁波(不要随便修改格式,否则.) 导行电磁波 —— 被限制在某一特定区域内传播的电磁波 导波系统 —— 引导电磁波从一处定向传输到另一处的装置 常用的导波系统的分类 :TEM 传输线、金属波导管、表面波导。 1. TEM 波传输线 平行双导线是最简单的 TEM 波传输线,随着工作频率的升高,其辐射损耗急剧增加,故双 导线仅用于米波和分米波的低频段。 同轴线没有电磁辐射,工作频带很宽。 2. 波导管 波导是用金属管制作的导波系统, 电磁波在管内传播,损耗很小, 主要用于 3GHz ~30GHz 的频 率范围。 本章内容 7.1 导行电磁波概论 7.2 矩形波导 7.3 圆柱形波导 7.4 同轴波导 7.5 谐振腔 7.6 传输线 7.1 导行电磁波概论 分析均匀波导系统时,做如下假定: 波导是无限长的规则直波导,其横截面形状可以任意,但沿轴向处处相同,沿 z 轴方向放 矩形波 导 圆波导

置。 波导内壁是理想导体,即0=0」 波导内填充均匀、线性、各向同性无耗媒质,其参数£、“和刀均为实常数 波导内无源,即p=0,J=0。 波导内的电磁场为时谐场。波沿+z方向传播。 1、场矢量 对于均匀波导,导波的电磁场矢量为 E(x,y,=)=E(x,y)e H(x,y,)=H(x,y)e 场分量: H,(x,y,2)=H,(x,y)e E,(x,y,=)=E,(x,y)er H,(x.y.=)=H,(x.y)er E,(xy,=)=E,(x,y)e-r H.(x,y,2)=H.(x,y)e E.(x,y,=)=E.(x,y)e 其中: E,(化八小E,(x,y小H,(G,少小H,(化八2)一横向分量 E.(xy,2人H(化,)-一纵向分量 横向场分量与纵向场分量的关系 足=y2+k月 E.+yE,-jouH. H(jo 0E.-Y H. V×E=-j9A= !直角坐标系中 aE2-正=-jouH 展开 H=jo6E, dy V×H=josE OHH.=-jocB, dx 明2=joeE .-jou- ,0 Ox a 导波的分类 如果E:=0,H:=0,E,H完全在横截面内,这种波被称为横电磁波,简记为EM波,这 种波型不能用纵向场法求解:
2 置。 波导内壁是理想导体,即 = 。 波导内填充均匀、线性、各向同性无耗媒质,其参数 、 和 均为实常数。 波导内无源,即 = 0, J = 0。 波导内的电磁场为时谐场。波沿 + z 方向传播。 1、场矢量 对于均匀波导,导波的电磁场矢量为 ( , , ) ( , )e ( , , ) ( , )e z z x y z x y x y z x y − − E E H H = = 场分量: ( , , ) ( , )e ( , , ) ( , )e ( , , ) ( , )e z x x z y y z z z H x y z H x y H x y z H x y H x y z H x y − − − = = = ( , , ) ( , )e ( , , ) ( , )e ( , , ) ( , )e z x x z y y z z z E x y z E x y E x y z E x y E x y z E x y − − − = = = 其中: E (x, y,z) E (x, y,z) H (x, y,z) H (x, y,z) x 、 y 、 x 、 y —— 横向分量 E (x, y,z) H (x, y,z) z 、 z —— 纵向分量 横向场分量与纵向场分量的关系 导波的分类 如果 Ez = 0, Hz = 0,E, H 完全在横截面内,这种波被称为横电磁波,简记为 TEM 波,这 种波型不能用纵向场法求解; = − E H j = H E j j j j z y x z x y y x z E E H y E E H x E E H x y + = − + = − = − j j j z y x z x y y x z H H E y H H E x H H E x y + = + = − − = 2 c 2 c 2 c 2 c 1 (j ) 1 (j ) 1 ( j ) 1 ( j ) z z x z z y z z x z z y E H H k y x E H H k x y E H E k x y E H E k y x = − − = + − = + − = − 直 角 坐标 系 中 展开 2 2 2 c k k = +

如果E,≠0,H,=0,传播方向只有电场分量,磁场在横截面内,称为横磁波,简称为M 波或E波: 如果E:=0,H:≠0,传播方向只有磁场分量,电场在横截面内,称为横电波,简称为TE波 或H波。 2. 场方程 根据亥姆霍兹方程 2E+k2E=0,V2H+2H=0 故场分量满足的方程 V2E,+k2E,=0,VH.+k2H.=0 72E.+k2E.=0,VH.+k2H.=0 一一横向场方程 V2E.+k2E.=0,V2H.+k2H=0 一一纵向场方程 电磁场的横向分量可用两个纵向分量表示,只需要考虑纵向场方程。 由于 a E.(x,y,=)=E.(x,y)e: F++)E,k,)=0 H.(x.y.=)=H.(x.y)e= a2a2 x++H.G川=0 72矩形波导 本节内容 7.2.】矩形波导中的场分布 7.2.2矩形波导中波的传播特性 723矩形波导中的主模 7.21矩形波导中的场分布 结构:如图所示,a一一宽边尺寸、b一一窄边尺寸 特点:可以传播TM波和TE波,不能传播TEM波 L.矩形波导中TM波的场分布:对于TM波,Hz=0,波导内的电磁场由Ez确定 方程,+ F+)E(G月=0 ,a2.a2 E.l-=0 E:l=0 边界条件:El,0=0E.l,6=0 利用分离变量法可求解此偏微分方程的边值问题。 设E具有分离变量形式,即E(x,)=fx)g)
3 如果 Ez 0, Hz = 0 ,传播方向只有电场分量,磁场在横截面内,称为横磁波,简称为 TM 波或 E 波; 如果 Ez = 0, Hz 0 ,传播方向只有磁场分量,电场在横截面内,称为横电波,简称为 TE 波 或 H 波。 2. 场方程 根据亥姆霍兹方程 0 0 2 2 2 2 E + E = H + H = k , k 故场分量满足的方程 —— 横向场方程 0 0 2 2 2 2 E z + k E z = , H z + k H z = —— 纵向场方程 电磁场的横向分量可用两个纵向分量表示,只需要考虑纵向场方程。 由于 7.2 矩形波导 本节内容 7.2.1 矩形波导中的场分布 7.2.2 矩形波导中波的传播特性 7.2.3 矩形波导中的主模 7.2.1 矩形波导中的场分布 结构:如图 所示,a ——宽边尺寸、 b ——窄边尺寸 特点:可以传播 TM 波和 TE 波,不能传播 TEM 波 1. 矩形波导中 TM 波的场分布:对于 TM 波,Hz = 0,波导内的电磁场由 Ez 确定 方程: 2 2 2 2 2 c ( ) ( , ) 0 z k E x y x y + + = 边界条件: | 0 | 0 | 0 | 0 0 0 = = = = = = = = z y z y b z x z x a E E E E 利用分离变量法可求解此偏微分方程的边值问题。 设 Ez 具有分离变量形式,即 E (x, y) f (x)g(y) z = 0 0 0 0 2 2 2 2 2 2 2 2 + = + = + = + = y y y y x x x x E k E H k H E k E H k H , , z z z z z z H x y z H x y E x y z E x y − − = = ( , , ) ( , )e ( , , ) ( , )e 2 2 2 2 2 c 2 2 2 2 2 c ( ) ( , ) 0 ( ) ( , ) 0 z z k E x y x y k H x y x y + + = + + = x y z O b a

代入到偏微分方程和边界条件中,得到两个常微分方程的固有值问题,即 f"(x)+k2f(x)=0 g"(y)+kig(y)=0 f0)=0,f(a)=0 g(0)=0,g(b)=0 两个固有值问题的解为一系列分离的固有值和固有函数: a f(x)=Asin(x) g(y)=Csin() a b 截止波数只与波导 的结构尺寸有关。 名=后+=+(爱 Ec)=fg0=E.sm受ng》 a 所以TM波的场分布 E(Gy=Ex水r=E.smT动snge a 器 匹,neog水” E)=尺69 a Hjsin)coye ke dy k2 b a b H,(xy)=- e-g6.o受m管水” kxka a H(x,y,)=0 m=1,2,3,.n=1,2,3,. m=1,2,3, 2.矩形波导中的T正波的场分布 n=1,2,3,. 对于TE波,E.=0,波导内的电磁场由H确定 m=1,2,3,. n=1,2,3,. 4
4 代入到偏微分方程和边界条件中,得到两个常微分方程的固有值问题,即 = = + = (0) 0, ( ) 0 ( ) ( ) 0 2 f f a f x k f x x = = + = (0) 0, ( ) 0 ( ) ( ) 0 2 g g b g y k g y y 两个固有值问题的解为一系列分离的固有值和固有函数: π π ( ) sin( ) x m k a m f x A x a = = π π ( ) sin( ) y n k b n g y C y b = = 故: 2 2 2 2 2 c π π ( ) ( ) mn xm yn m n k k k a b = + = + π π ( , ) ( ) ( ) sin( )sin( ) z m m n E x y f x g y E x y a b = = 所以 TM 波的场分布 m π π ( , , ) ( , )e sin( )sin( )e z z z z m n E x y z E x y E x y a b − − = = 2 2 m c c 2 2 m c c 2 2 m c c 2 2 m c c π π π ( , , ) cos( )sin( )e π π π ( , , ) sin( )cos( )e j j π π π ( , , ) sin( )cos( )e j j π ( , , ) cos( z z x z z y z z x z y E m m n E x y z E x y k x k a a b E n m n E x y z E x y k y k b a b E n m n H x y z E x y k y k b a b E m H x y z E k x k a − − − = − = − = − = − = = = − = − π π )sin( )e ( , , ) 0 z z m n x y a b H x y z − = m =1 2 3, , n =1 2 3, , 2. 矩形波导中的 TE 波的场分布 对于 TE 波, E z = 0 ,波导内的电磁场由 Hz 确定 m =1 2 3, , n =1 2 3, , m =1 2 3, , n =1 2 3, , 截止波数只与波导 的结构尺寸有关

02 方程:+ +k)H.(x,)=0 Ox Ox -00 边界条件:可少 a H.( 其解为: a 6以 m=01,2,3,. 受+学 m=0,l,2,3,. 所以TE波的场分布 H.(x.y.)=H cos(x)cos( a 6e H,x,)=名mHsn k2 a x)cos( 6 e H,老gH.o受s爱水” k2 b a E(x:v.=Omc0s(S方2 k2 b a F.incod ye" k2 a E.(x,y,z)=0 m=0,1,2,3.·n=0,l,2,3.· 3.矩形波导中的TM波和T正波的特点 m和n有不同的取值,对于m和n的每一种组合都有相应的截止波数Kn和场分布,即 一种可能的模式,称为TMm模或TEmn模: 不同的模式有不同的截止波数Kmm:
5 方程: 2 2 2 2 2 c ( ) ( , ) 0 z k H x y x y + + = 边界条件: | 0 | 0 | 0 | 0 0 0 = = = = = = = = y b z y z x a z x z y H y H x H x H 其解为: m π π ( , ) cos( )cos( ) z m n H x y H x y a b = m = 0 1 2 3, , 2 2 c π π ( ) ( ) mn m n k a b = + m = 0 1 2 3, , 所以 TE 波的场分布 m π π ( , , ) cos( )cos( )e z z m n H x y z H x y a b − = 2 m c 2 m c 2 m c 2 m c π π π ( , , ) sin( )cos( )e π π π ( , , ) cos( )sin( )e j π π π ( , , ) cos( )sin( )e j π π π ( , , ) sin( )cos( )e ( , , ) 0 z x z y z x z y z m m n H x y z H x y k a a b n m n H x y z H x y k b a b n m n E x y z H x y k b a b m m n E x y z H x y k a a b E x y z − − − − = = = = − = m = 0 1 2 3, , n = 0 1 2 3, , 3. 矩形波导中的 TM 波和 TE 波的特点 m 和 n 有不同的取值,对于 m 和 n 的每一种组合都有相应的截止波数 Kcmn 和场分布,即 一种可能的模式,称为 TMmn 模或 TEmn 模; 不同的模式有不同的截止波数 Kcmn ;

由于对相同的m和n,TM模和TE,模的截止波数K相同,这种情况称为模式的简 并: 对于TEmn模,其m和n可以为O,但不能同时为0:而对于TMm模,其m和n不能为 O,即不存在TMmo模和TMm模。 7.2.2矩形波导中波的传播特性 在矩形波导中,TEm波和TMm波的场矢量均可表示为 E.(x.y.)=E(x.y)ei H(x.y.)=H(x.y)ewi 式中:ym=Vn-及=V尽-oE 矩形波导中的TEm波和TM一波的传播特性与电磁波的波数k和截止波数人m有关。 当kn>k时,m为实数,e为衰减因子。二 ·相应模式的波不能在矩形波导中传 纯虚数八、 ou Y.k-(k./k) 当km=k时,m=0,一一相应模式的波也不能在矩形波导中传播。 由k=k=o压定义 k。 + 截止角频率: o.ea 1 + 截止频率: 2π√ue2π√eVa 2π 2π 截止波长: -kma+mb'f-压 结论:在矩形波导中,TE0模的截止频率最低、截止波长最长。 6
6 由于对相同的 m 和 n,TMmn 模和 TEmn 模的截止波数 Kcmn 相同, 这种情况称为模式的简 并; 对于 TEmn 模,其 m 和 n 可以为 0,但不能同时为 0;而对于 TMmn 模, 其 m 和 n 不能为 0,即不存在 TMm0 模和 TMon 模。 7.2.2 矩形波导中波的传播特性 在矩形波导中, TEmn 波和 TMmn 波的场矢量均可表示为 ( , , ) ( , )e ( , , ) ( , )e mn mn z z mn mn mn mn x y z x y x y z x y − − E E H H = = 式中: 2 2 2 2 mn mn mn c c = − = − k k k 矩形波导中的 TEmn 波和 TMmn 波的传播特性与电磁波的波数 k 和截止波数 cmn k 有关。 当 k k cmn 时, mn 为实数, mnz e − 为衰减因子。 —— 相应模式的波不能在矩形波导中传 播。 波阻抗 : 2 TM c 1 ( ) j j mn mn mn k Z k k = = − TE 2 c j j 1 ( ) mn mn mn Z k k k = = − 当 k k cmn = 时, mn = 0 ,—— 相应模式的波也不能在矩形波导中传播。 由 cmn k k = = 定义 截止角频率: c 2 2 c 1 π π ( ) ( ) mn mn k m n a b = = + 截止频率: c 2 2 c 1 π π ( ) ( ) 2π 2π mn mn k m n f a b = = + 截止波长: c 2 2 c c 2π 2π 1 ( π ) ( π ) mn mn mn k m a n b f = = = + 结论:在矩形波导中, TE10 模的截止频率最低、截止波长最长。 纯虚数

当太 波阻抗: 是点层 Zn-iou-on= 0μ Ak-厉>V台 结论: 当工作频率∫大于截止频率时,矩形波导中可以传播相应的TEm模式和TM-模式的 电磁波: 当工作频率∫小于或等于截止须率m时,矩形波导中不能传播相应的TEm模式和 TMm模式的电磁波。 例72.1在尺寸为a×b=2.86mm×10.16mm的矩形波导中,传输TEo模,工作频率 10GHz。 (1)求截止波长、波导波长和波阻抗: (2)若波导的宽边尺寸增大一倍,上述参数如何变化?还能传输什么模式? (3)若波导的窄边尺寸增大一倍,上述参数如何变化?还能传输什么模式? 解:(1)截止波长 o=2a=2×22.86=45.72mm
7 当 k k cmn 时, 2 2 2 2 2 c π π j ( ) ( ) j mn mn mn m n k k a b = − = − − = —— 相应模式的波能在矩形波导中传播。 传播参数 相位常数: 2 2 2 2 c 2 2 c c π π ( ) ( ) 1 ( / ) 1 ( / ) 1 ( / ) mn mn mn mn m n k k k a b k f f k = − − = − = − = − 相速: p 2 c 1 ( / ) mn mn mn v k f f k = = − 波导波长: g 2 c 2π 2π 2π 1 ( / ) mn mn k f f k = = − 波阻抗: 2 TM c 1 ( ) j mn mn mn mn k Z f f = = = − TE 2 c j 1 ( ) mn mn mn mn Z k f f = = = − 结论: 当工作频率 f 大于截止频率 cmn f 时,矩形波导中可以传 播相应的 TEmn 模式和 TMmn 模式的 电磁波; 当工作频率 f 小 于或等于截止频率 cmn f 时,矩形波导中不能传播相 应的 TEmn 模式和 TMmn 模式的电磁波。 例 7.2.1 在尺寸为 a b = 22.86mm 10.16mm 的矩形波导中,传输 TE10 模,工作频率 10GHz。 (1)求截止波长、波导波长和波阻抗; (2)若波导的宽边尺寸增大一倍,上述参数如何变化?还能传输什么模式? (3)若波导的窄边尺寸增大一倍,上述参数如何变化?还能传输什么模式? 解:(1)截止波长 c10 = = = 2 2 22.86 45.72 mm a

3×108 Jm-2a/42x226x10656x10'h 3×10-2 10= =3.97×10-2m V1-(o/fV-(6.56/10 no 37=49939 Z-1万0755 (2)当4=2a=2×22.86=45.72mm时 入o=2d=91.44mm 1 fao=2doo =1×6.56×10°=3.28×10°Hz 2 3×102 g10= =3.176×10-2m 1-(feo/f) V-(3.28/10y 377 Z-无m03920 无-d452m,不号知-048m 由于工作波长:元=30mm 故此时能传输的模式为:TE0TE0TE0 (3)当6'=2b=2×10.16=20.32mm时 1 =6.56×10°Hz 元o=2a=45.72mm feo-2aHoo hw-(faul =397x102mZ-a1万 =499.32 此时:乙o1=2b'=40.64mm
8 8 9 10 3 0 0 1 3 10 6.56 10 Hz 2 2 22.26 10 c f a − = = = 2 0 2 g10 2 2 c10 3 10 3.97 10 m 1 ( ) f f 1 (6.56 10) − − = = = − − 10 0 TE 2 c10 377 499.3 1 ( ) 0.755 Z f f = = = − (2)当 a a = = = 2 2 22.86 45.72 mm 时 c10 = = 2 91.44 mm a 9 9 c10 0 0 1 1 6.56 10 3.28 10 Hz 2 2 f a = = = 2 0 2 g10 2 2 c10 3 10 3.176 10 m 1 ( ) 1 (3.28 10) f f − − = = = − − 10 0 TE 2 c10 377 399.2 1 ( ) 0.892 Z f f = = = − 此时: c20 = = a 45.72 mm , c30 2 30.48 mm 3 = = a 由于工作波长: = 30 mm 故此时能传输的模式为: TE TE TE 10 20 30 、 、 (3)当 b b = = = 2 2 10.16 20.32 mm 时 c10 = = 2 45.72 mm a , 9 c10 0 0 1 6.56 10 Hz 2 f a = = 0 2 g10 2 c10 3.97 10 m 1 ( ) f f − = = − 10 0 TE 2 c10 499.3 1 ( ) Z f f = = − 此时: c01 = = 2 40.64 mm b

2 2 en=1 :=30.4mm Wa+(B)/22.86)+y20.32) 由于工作波长:1=30mm 故此时能传输的模式为:TE0 TEor TE,n、TM, 7.2.3矩形波导中的主棋 主模:截止频率最低的模式 高次模:除主模以外的其余模式 在矩形波导中(a>b):主模为TE。模 若a>2b,TEo模为第一个高次模 若b<a<2b,TEo,模为第一个高次模 TE。模(主模)的传播特性参数 kao=a Jao2a eu kin=2a Bo=yo ns-(nla) 主模的场结构 对于主模TE。模,电磁场分量复数形式为 H.(x,y,=)=H cos(x)e E(xy,)=0 E(xy,)=-jaL H sin()e π H,(k,y)=jH。,sin)-e H(x,y,z)=0 E.(x,y,z)=0 对于主模TE。模,电磁场分量瞬时值形式为 9
9 ( ) ( ) ( ) ( ) c11 2 2 2 2 2 2 30.4 mm 1 1 1 22.86 1 20.32 a b = = = + + 由于工作波长: = 30 mm 故此时能传输的模式为: TE TE TE TM 10 01 11 11 、 、 、 7.2.3 矩形波导中的主模 主模:截止频率最低的模式 高次模:除主模以外的其余模式 在矩形波导中 (a b) :主模为 TE10 模 若 a 2b,TE20 模为第一个高次模 若 b a 2b ,TE01 模为第一个高次模 TE10 模(主模)的传播特性参数 c10 π k a = , c10 1 2 f a = , c10 = 2a , ( ) 2 2 10 = − π / a 主模的场结构 对于主模 TE10 模,电磁场分量复数形式为 j m j m j m π ( , , ) cos( )e ( , , ) 0 π ( , , ) j sin( )e π π ( , , ) j sin( )e π ( , , ) 0 ( , , ) 0 z z x z y z x y z H x y z H x a E x y z a E x y z H x a a H x y z H x a H x y z E x y z − − − = = = − = = = 对于主模 TE10 模,电磁场分量瞬时值形式为
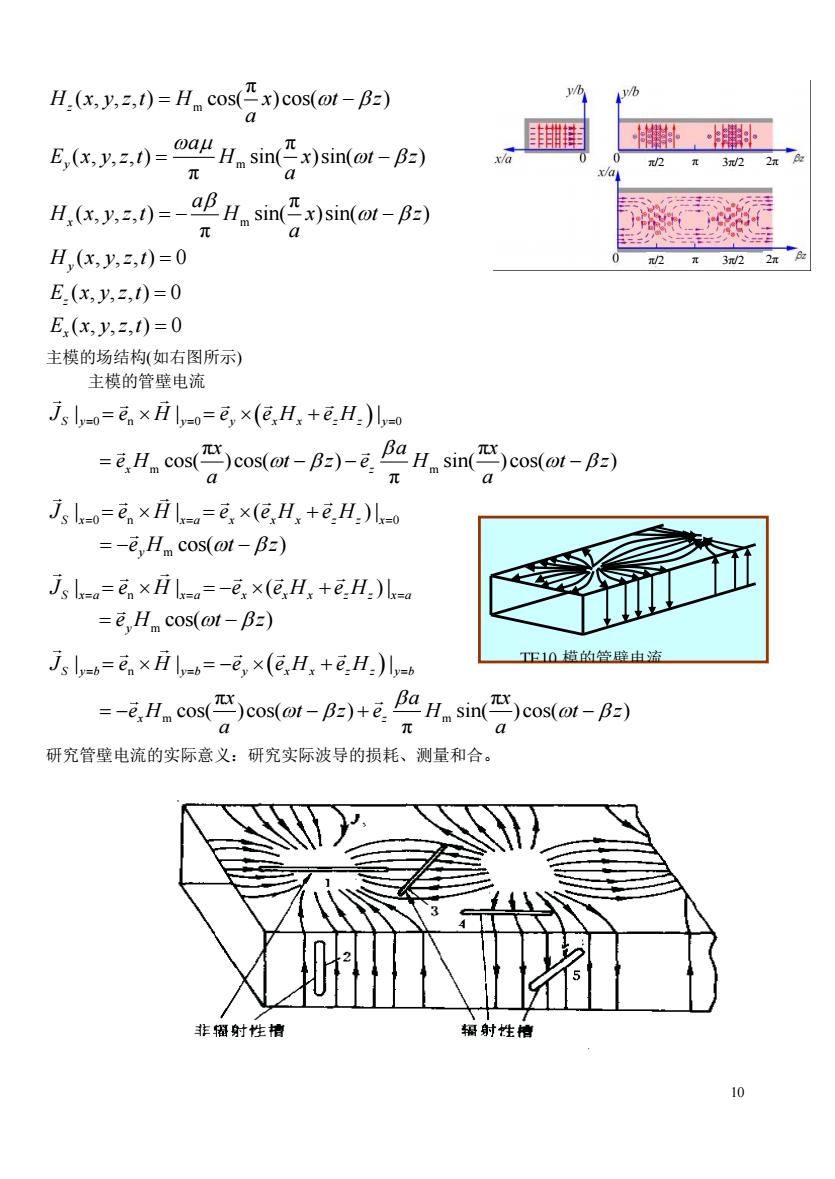
H.(cy三0=o)co-) y E=0-ogH.sm刘sam- 2有322 H.y.Hsin(x)sin(ot-Bz) a H.(x,y,=,t)=0 2x322 E.(x,y,z,t)=0 E(x,y,2,t)=0 主模的场结构(如右图所示) 主模的管壁电流 j,l,o=元×ilo=e,×(eH+eH)儿,0 =.co)co-A)-eg.i)cole似-A Jlo=e×Hla=E×(eH+EH)儿0 =-e,H cos(ot-Bz) Jsl=exHLa=-e,x(e,H,+e.H.)o =e,H cos(ot-B=) Jsl=b=en×Hl-b=-e×(eH.+eH)儿eb T正10描的管由洁 co cos+.Ba Hsin()cos(z) 研究管壁电流的实际意义:研究实际波导的损耗、测量和合。 菲射性槽 辐射性槽 10
10 m m m π ( , , , ) cos( )cos( ) π ( , , , ) sin( )sin( ) π π ( , , , ) sin( )sin( ) π ( , , , ) 0 ( , , , ) 0 ( , , , ) 0 z y x y z x H x y z t H x t z a a E x y z t H x t z a a H x y z t H x t z a H x y z t E x y z t E x y z t = − = − = − − = = = 主模的场结构(如右图所示) 主模的管壁电流 0 n 0 0 ( ) m m | | | π π cos( )cos( ) sin( )cos( ) π S y y y x x z z y x z J e H e e H e H x a x e H t z e H t z a a = = = = = + = − − − 0 n 0 m | | ( ) | cos( ) S x x a x x x z z x y J e H e e H e H e H t z = = = = = + = − − n m | | ( ) | cos( ) S x a x a x x x z z x a y J e H e e H e H e H t z = = = = = − + = − n ( ) m m | | | π π cos( )cos( ) sin( )cos( ) π S y b y b y x x z z y b x z J e H e e H e H x a x e H t z e H t z a a = = = = = − + = − − + − 研究管壁电流的实际意义:研究实际波导的损耗、测量和合。 π/2 π 3π/2 2π π/2 π 3π/2 2π π/2 π 3π/2 2π TE10 模的管壁电流