
中国石油大学 CHINA UNIVERSITY OF PETROLEUM 近代物理实验(3) 氢原子光谱与里德伯常数的测定 闫向宏 物理科学与技术学院近代物理实验室
氢原子光谱与里德伯常数的测定 近代物理实验(3) 闫向宏

氢原子光谱与里德伯常数的测定 Johann Jakob Balmer Johannes Rober Rydberg 1825~1898 1854~1919 瑞士数学兼物理学家 瑞典物理学家、数学家,光谱学 的奠基人之一
氢原子光谱与里德伯常数的测定 Johann Jakob Balmer 1825 ~1898 瑞士数学兼物理学家 Johannes Rober Rydberg 1854~1919 瑞典物理学家、数学家,光谱学 的奠基人之一

氢原子光谱与里德伯常数的测定 ▣实验目的 1、通过测量氢光谱(在可见光区域)谱线的 波长,验证巴尔末规律的正确性。 2、测定氢的里德伯常数,并与理论值进行对 比,对近代测量精度有初步了解。 实验仪器 氢光源、WGD-8A型光栅光谱仪
实验目的 1、通过测量氢光谱(在可见光区域)谱线的 波长,验证巴尔末规律的正确性。 2、测定氢的里德伯常数,并与理论值进行对 比,对近代测量精度有初步了解。 实验仪器 氢光源、WGD-8A型光栅光谱仪 氢原子光谱与里德伯常数的测定
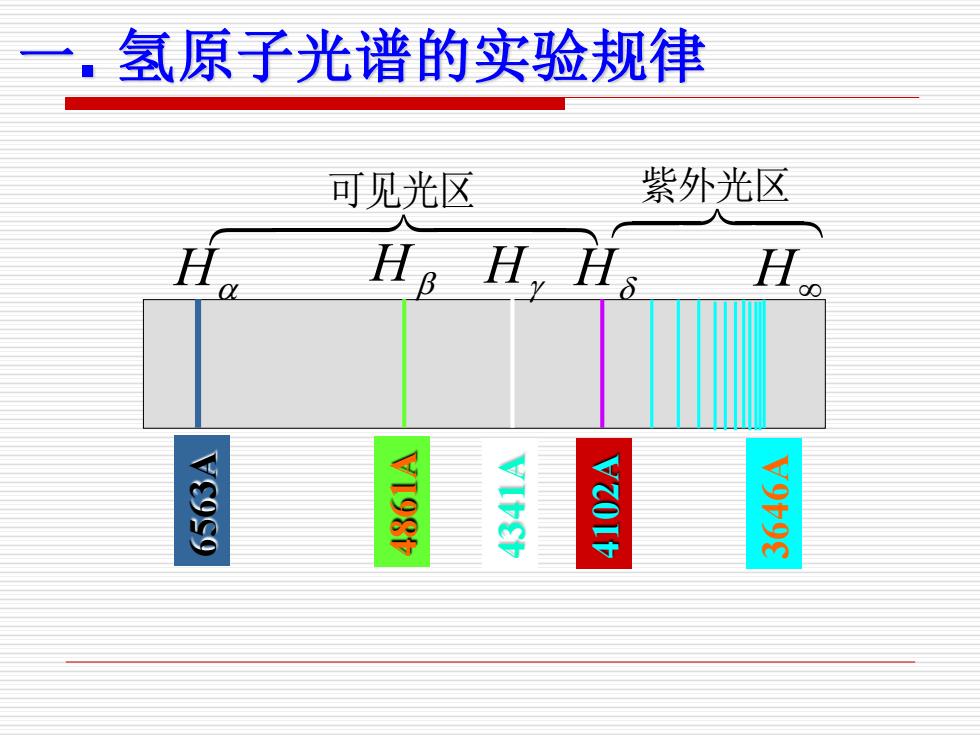
.氢原子光谱的实验规律 可见光区 紫外光区 H。H,H、 H. 43S9 930
一 . 氢原子光谱的实验规律 H H H H H 6563A 4861A 4341 A 4102 A 3646 A 可见光区 紫外光区

.氢原子光谱的实验规律 1885年瑞士的巴耳末用经验公式表示出氢 原子的前四条可见光谱: 九=B 2-4 巴耳末公式 n=3,4,5,6
1885年瑞士的巴耳末用经验公式表示出氢 原子的前四条可见光谱: 4 2 2 − = n n B n = 3,4,5,6 -巴耳末公式 一 . 氢原子光谱的实验规律

氢原子光谱的实验规律 1889年瑞典物理学家里德伯提出一个普遍 方程 里德伯公式 k=1,2,·n>k的整数 R=1.096776x103m 里德伯常量
1889年瑞典物理学家里德伯提出一个普遍 方程 ) 1 1 ( ~ 2 2 k n = R − R=1.096776107m-1 -里德伯公式 -里德伯常量 k =1,2, n k 的整数 一 . 氢原子光谱的实验规律

.氢原子光谱的实验规律 不同的k对应不同的谱系;当k一定时,每一n 值对应于一条谱线 0k=1,n=23.莱曼系,紫外区 2k=2,n=3,4,.巴尔末系 3k=3,n=4,5,.帕邢系,红外区 ④k=4,n=5,6,.布拉开系红外区 5k=5,n=6,7,.普丰德系,红外区
k=1,n=2,3,. 莱曼系,紫外区 k=2,n=3,4,. 巴尔末系 k=3,n=4,5,. 帕邢系,红外区 k=4,n=5,6,. 布拉开系,红外区 k=5,n=6,7,. 普丰德系,红外区 不同的k对应不同的谱系;当k一定时,每一n 值对应于一条谱线 一 . 氢原子光谱的实验规律

氢原子光谱的实验规律 里德伯常数的理论值: 由波尔氢原子理论可知:氢原子从高能级En跃迁 到低能级Ek时,发射谱线的波数为 2π2e4m 2π2em RH= 由此可知里德伯常数理论值为 (4π6}ch|1+ m
一 . 氢原子光谱的实验规律 由波尔氢原子理论可知:氢原子从高能级En跃迁 到低能级Ek时,发射谱线的波数为 ( ) − + = 2 2 2 3 0 2 4 1 2 1 4 1 1 2 n M m ch e m H 由此可知里德伯常数理论值为 ( ) + = H H M m ch e m R 4 1 2 2 3 0 2 4 里德伯常数的理论值:

二.实验注意事项 1.本实验采用了计算机辅助测量光谱线的波场值,因 此与铁原子光谱有关的内容取消。 2.打开光栅光谱仪和氢光灯电源,预热仪器。 3.自学WGD-8A型光栅光谱仪说明书以及相关软件 使用操作手册,正确掌握仪器使用方法。 4.正确判断谱线级数n,并多次测量谱线波长,选择 合适的数据处理方法,计算里德伯常量
二. 实验注意事项 1. 本实验采用了计算机辅助测量光谱线的波场值,因 此与铁原子光谱有关的内容取消。 2. 打开光栅光谱仪和氢光灯电源,预热仪器。 3. 自学WGD-8A型光栅光谱仪说明书以及相关软件 使用操作手册,正确掌握仪器使用方法。 4. 正确判断谱线级数n,并多次测量谱线波长,选择 合适的数据处理方法,计算里德伯常量

三.氢原子光谱实验实物图 #柱君日
三. 氢原子光谱实验 实物图