
32-4能量守恒定律 2-4-1功和功率 功是度量能量转换的基本物理量,它反映了力 对空间的累积作用。 功的定义: 在力F的作用下, 物体发生了位移△产,则 把力在位移方向的分力与 位移△下的乘积称为功
§2-4 能量守恒定律 2-4-1 功和功率 功是度量能量转换的基本物理量,它反映了力 对空间的累积作用。 功的定义: 在力 的作用下, 物体发生了位移 ,则 把力在位移方向的分力与 位移 的乘积称为功。 F r r x y z O 1 r r F F

W=F△rcos0=F.△ 国际单位制单位:焦耳(J) 质点由a点沿曲线运动到b点的过程中,变力所 做的功。 元功:dW=F.d w=心F.dr=Fs
W F r θ F r = Δ cos = Δ 国际单位制单位:焦耳(J ) a b F r d 质点由a点沿曲线运动到b点的过程中,变力 所 做的功 。 F 元功: W F r d = d = = b a b a W F r F r d cos d

合力的功: W=心F.d正=心匠+五++f) rd+万d++万d w=W+w,+.+W 结论:合力对质点所做的功等于每个分力对质点 做功之代数和
合力的功: W F r (F F F ) r b a n b a = d = 1 + 2 + + d = + + + b a n b a b a F r F r F r 1 d 2 d d W =W1 +W2 ++Wn 结论:合力对质点所做的功等于每个分力对质点 做功之代数和

在直角坐标系Ogyz中 F=Fi+Fj+Fk 下=xi+刀+z水 W=["F.dF =[F+J+FR)(dxi+dj+d-) =∫Fdk+Fd少+Fd起
在直角坐标系Oxyz中 F F i F j F k x y z = + + r xi yj zk = + + ( ) ( ) F x F y F z W F r F i F j F k xi yj zk y z b a x b a x y z b a d d d d d d d = + + = = + + + +

功率是反映做功快慢程度的物理量。 功率:单位时间内所做的功。 平均功率:下= △W 单位:W=Js △t 瞬时功率: P=lim △WdW △1→0 △t di dW_F山=方.⑦ dt dt
功率是反映做功快慢程度的物理量。 功率:单位时间内所做的功。 平均功率: t W P = 瞬时功率: t W t W P t d d lim 0 = = → 单位:W = J·s -1 v = = = F t F r t W P d d d d

例1设作用在质量为2kg的物体上的力F=6tN。如 果物体由静止出发沿直线运动,在头2s内这力做了 多少功? 解: F 6t dv a= 3t .:a= m 2 dt do adt 3t dt 两边积分: 3 2 dx 3 0三 dx odt >1'dt dt 2 w-frd-Carra- =36J
例1 设作用在质量为2kg的物体上的力F = 6t N。如 果物体由静止出发沿直线运动,在头2 s内这力做了 多少功? 解: t t m F a 3 2 6 = = = t a d dv = dv = adt = 3t dt 两边积分: = t t t 0 0 d 3 d v v 2 2 3 v = t t x d d v = x t t dt 2 3 d d 2 = v = 2 0 4 2 0 2 4 9 d 2 3 W = F dx = 6t t t = t = 36 J

2-4-2 动能和动能定理 1.质点动能定理 动能:质点因有速度而具有的对外做功本领。 单位:J 设质点m在力的作用下沿曲 线从a点移动到b点 元功: dw F.dr Fcosads
2-4-2 动能和动能定理 动能: 质点因有速度而具有的对外做功本领。 2 k 2 1 E = mv 单位:J 设质点m在力的作用下沿曲 线从a点移动到b点 元功: dW = F dr = F cos ds r d F a b 1.质点动能定理

dv F cosa=ma m dt dw =F cosads m g玉=mwd 总功:F=jdW=mod=mc好-d) 质点的动能定理: 合外力对质点所做的功等于质点动能的增量。 W= m-2m=E-E
总功: ( ) 2 1 d d 2 1 2 2 2 1 v v v v v v = = = − W W m m 质点的动能定理: 合外力对质点所做的功等于质点动能的增量。 k2 k1 2 1 2 2 2 1 2 1 W = mv − mv = E − E v v v d d d d d cos d s m t W = F s = m = t F ma m d d cos t v = =
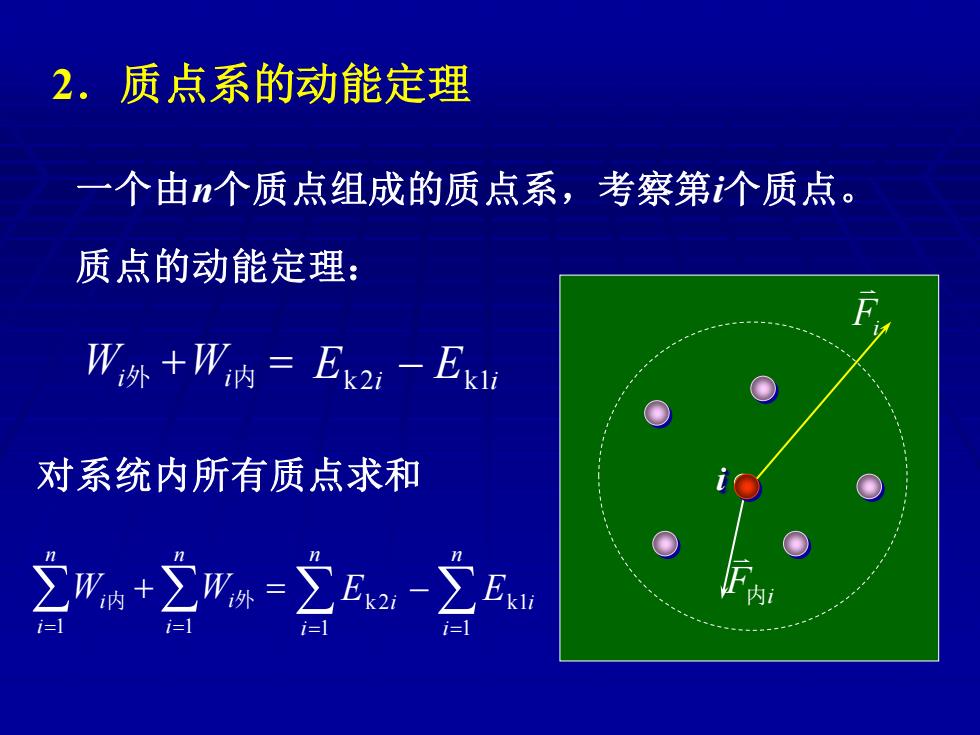
2.质点系的动能定理 一个由个质点组成的质点系,考察第个质点。 质点的动能定理: W,外+W内=E2-E 对系统内所有质点求和 W+-E立
2.质点系的动能定理 i Fi F内i 一个由n个质点组成的质点系,考察第i个质点。 质点的动能定理: Ek2i − Ek1i 外 + 内 = Wi Wi 对系统内所有质点求和 = = − n i i n i E i E 1 k1 1 k2 + = = = n i n i Wi Wi 1 1 内 外

W内+W外=E2一Ek1 质点系的动能定理: 质点系动能的增量等于作用于系统的所有外力和 内力做功之代数和。 值得注意: 内力做功可以改变系统 的总动能
Ek2 − Ek1 W内 +W外 = 质点系动能的增量等于作用于系统的所有外力和 内力做功之代数和。 质点系的动能定理: 内力做功可以改变系统 的总动能。 值得注意: