《大学物理》课程教学课件（PPT讲稿，高教版）1-3 圆周运动

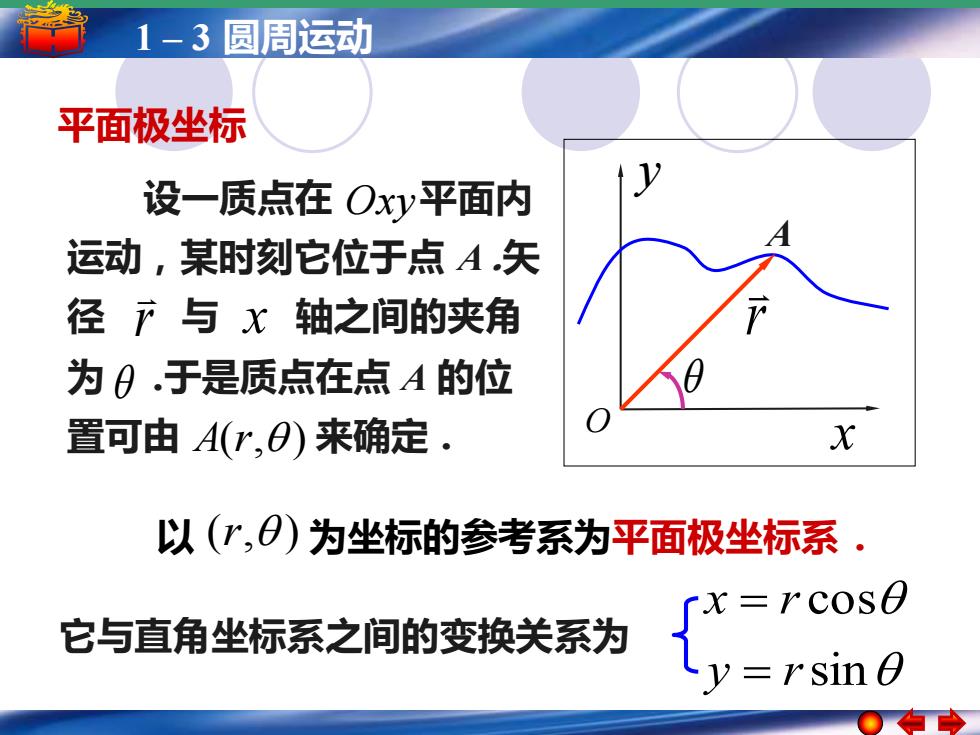
1-3圆周运动 平面极坐标 设一质点在Oxy平面内 运动，某时刻它位于点A矢 径下与x轴之间的夹角 为日.于是质点在点A的位 置可由A(r,)来确定. X 以(”，)为坐标的参考系为平面极坐标系. 「x=rc0SO 它与直角坐标系之间的变换关系为 =rsin

1 – 3 圆周运动 x y O 平面极坐标  A r  设一质点在 平面内 运动，某时刻它位于点 A .矢 径 与 轴之间的夹角 为 .于是质点在点 A 的位 置可由 A(r, ) 来确定 . Oxy r  x  以 (r, ) 为坐标的参考系为平面极坐标系 .   sin cos y r x r = = 它与直角坐标系之间的变换关系为

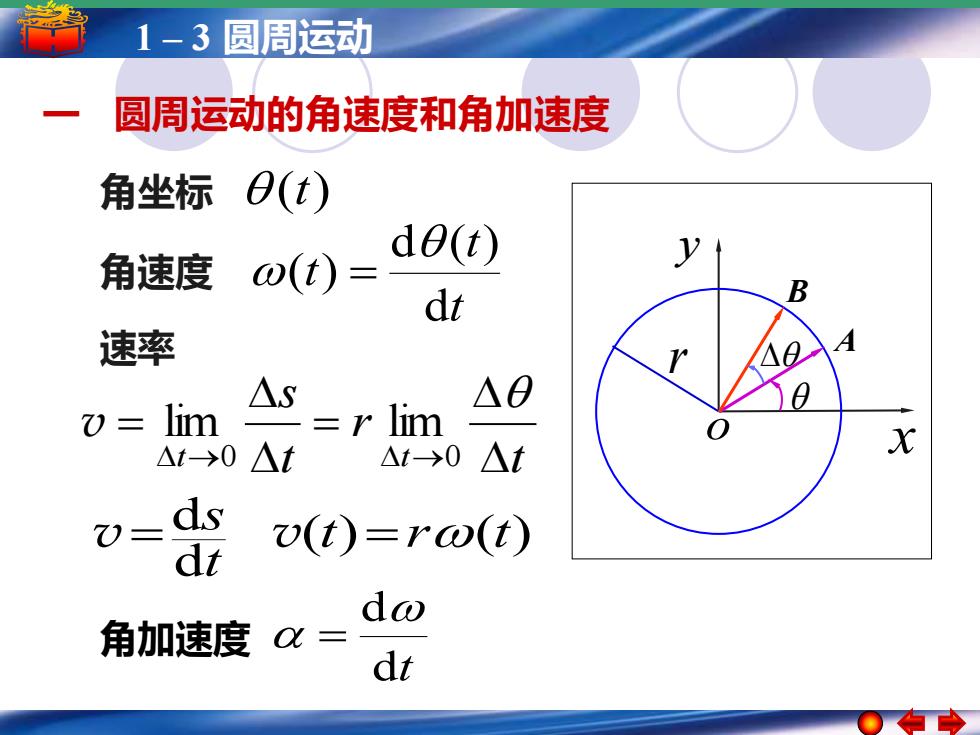
1-3圆周运动 圆周运动的角速度和角加速度 角坐标O(t) de(t) 角速度 o(t)= dt 速率 △S △0 )= lim =r lim △t→0△t △t→0△t ds v(t)=ra(t) dw 角加速度 x= dt

1 – 3 圆周运动 一 圆周运动的角速度和角加速度 t t t d d ( ) ( )  角速度  = 角坐标  (t) 角加速度 dt d  = x y o r ( ) ( ) d d t r t t v= s v =   A  B 速率 t r t s t t   =   =  →  →  0 0 v lim lim

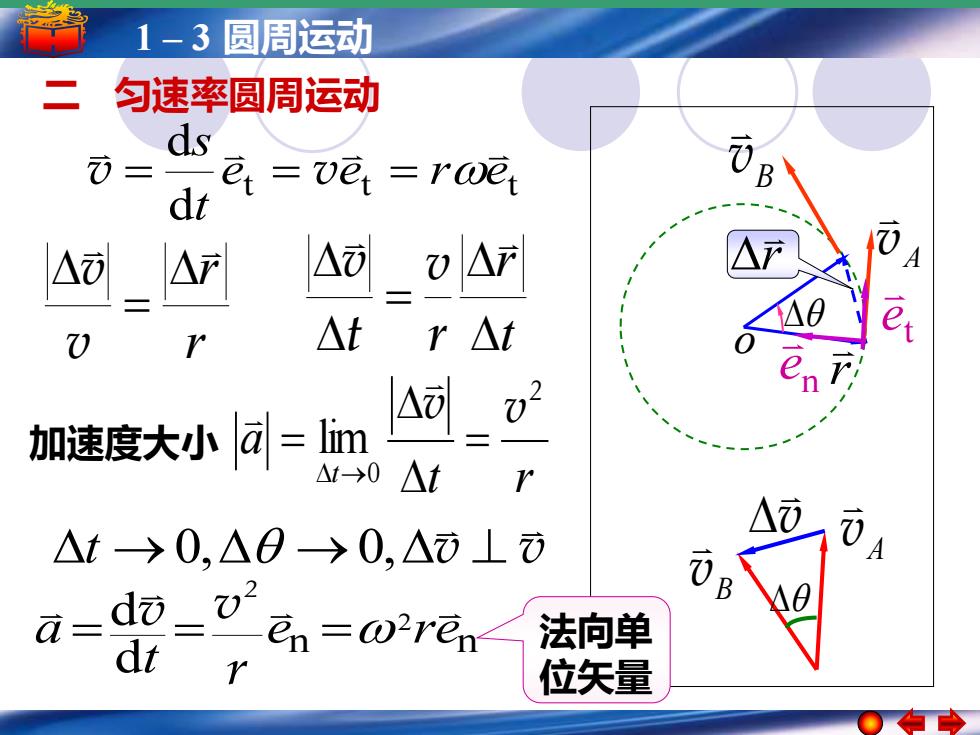
1-3圆周运动 二 匀速率圆周运动 ds )= e ve rwe dt 71 △) △产 △⑦ 0△F △t r△t e, 02 加速度大小d=lim A △1-→0 △t △ò △t→0，△0>0，△市⊥ 0 Q- do_v d en -@'rem 法向单 位矢量

1 – 3 圆周运动 t t t d d e e r e t  s    v = = v =  n n 2 d d e re t a     = = = r v v 2 t r a t 2 v v =   =  →   0 加速度大小 lim r r    =  v v t r   =     r v t v v v   t →0, →0, ⊥ 二 匀速率圆周运动  B v  A v  v   法向单 位矢量 A v  r o   B v  r   t e  n e 

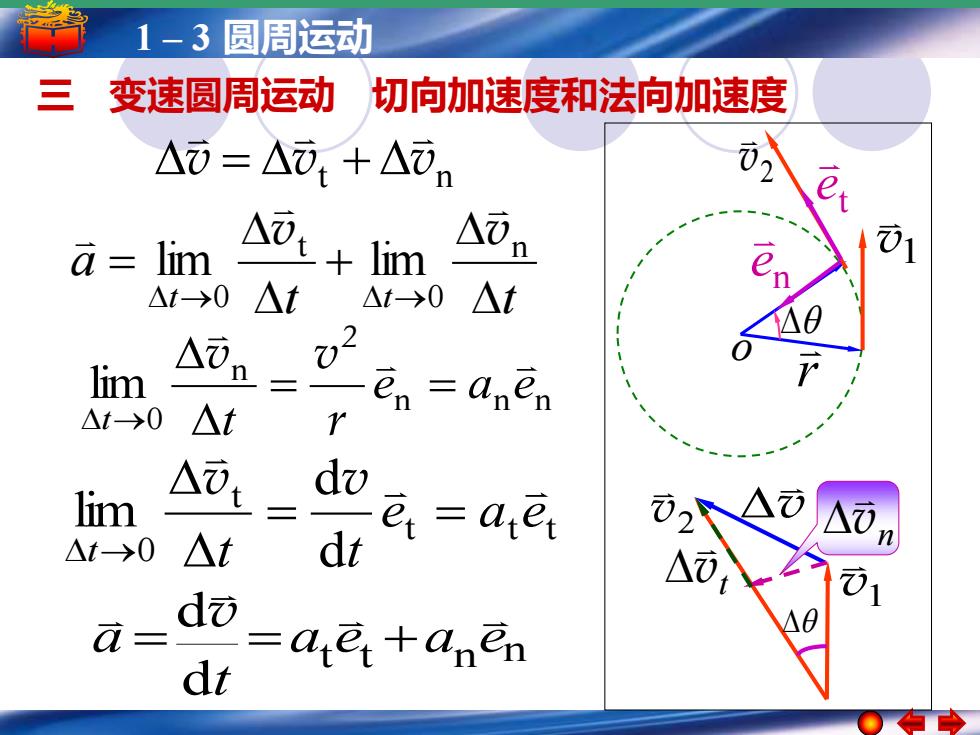
1-3圆周运动 三 变速圆周运动 切向加速度和法向加速度 △=△，+△in a- lim +lim △i △t→0 △t △t-→0△t lim △in = en anen △t-→0△t Y dv lim -arer △t→0 △t dt △i dò a ae+anen dt

1 – 3 圆周运动 v1   v2  v   v1  r o   2 v  n v   t v   v vt vn     =  +  t t n n d d a e a e t a     = = + v t t a t t   +   =  →  → n 0 t 0 lim lim v v    三 变速圆周运动 切向加速度和法向加速度 t e  n e  n n n n 0 lim e a e t t    = =    → r v v 2 t t t t 0 d d lim e a e t t t    = =    → v v

1-3圆周运动 切向加速度（速度大小变化引起） 4-=u- dr2 法向加速度（速度方向变化引起） a=00=02r= 02 r >圆周运动加速度 a-ae +anen 02 dv △ 二 e+—En dt r a=√a+a

1 – 3 圆周运动 切向加速度（速度大小变化引起） 2 2 t d d d d t s r t a = =  = v 法向加速度（速度方向变化引起） r a r 2 2 n v = v = = a at et an en    = + ➢ 圆周运动加速度 2 2 a= at +an v1  r o   2 v  v1   v2  v   n v   t v   n 2 t d d e r e t v  v  = + t e  n e 

1-3圆周运动 a-ae+a en a与e,夹角B=arctan .am>0.0切向加速度 dt =r0 0, >0,0<B<乃0增大 n X =0,B=买，=常量 <0,<B<元，减小

1 – 3 圆周运动 ➢ 切向加速度 r t a = = d d t v π, v 2 π 0,    减小 at , v 增大 2 π 0, 0   , 常量 2 =0,  =π v a    a  an 00 π v  t e  en  x y o a at et a n en    = + 与 夹角 t arctan n a a a  =  t e  a 

1-3圆周运动 对于一般的曲线运动 dt 其中p ds 曲率半径 利用自然坐标，一切运动可以 根据切向、法向加速度来分类 : an=0 a=0 匀速直线运动 0n=0 04≠0 变速直线运动 a与a,的夹角 0m≠0 04=0 匀速曲线运动 tan⑩= 0n≠0 44≠0 变速曲线运动

1 – 3 圆周运动 t n d d e e t a     2 v v t = + d d e t s   v=   d ds 其中 = 曲率半径 . t n t tan a a a a  = 与 的夹角   a  n a  t a   ➢ 对于一般的曲线运动 利用自然坐标, 一切运动可以 根据切向、法向加速度来分类： an= 0 at= 0 匀速直线运动 an= 0 at  0 变速直线运动 an  0 at = 0 匀速曲线运动 an  0 at  0 变速曲线运动

1-3圆周运动 讨论 对于作曲线运动的物体，以下几种说法中哪一种 是正确的： (A)切向加速度必不为零 大(B)法向加速度必不为零（拐点处除外） (C)由于速度沿切线方向，法向分速度必为零 因此法向加速度必为零 (D)若物体作匀速率运动，其总加速度必为零 (E)若物体的加速度为常矢量，它一定作匀变 速率运动

1 – 3 圆周运动 对于作曲线运动的物体，以下几种说法中哪一种 是正确的： （A）切向加速度必不为零 （B）法向加速度必不为零（拐点处除外） （C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零 （D）若物体作匀速率运动，其总加速度必为零 （E）若物体的加速度 为常矢量，它一定作匀变 速率运动 a  讨 论

1-3圆周运动 讨论 例质点作半径为的变速圆周运动的加速 度大小为 dv (A) (B) dr R (C) 2 dt R ★m的+(

1 – 3 圆周运动 例 质点作半径为R的变速圆周运动的加速 度大小为 （A） （B） （C） （D） dt dv R 2 v R v v 2 + dt d 2 2 ) ( ) d d ( R v v 2 + t 讨 论

1-3圆周运动 例1设有一个质点作半径为r的圆周运动.质点沿 圆周运动所经历的路程与时间的关系为s=b2/2,并设b 为一常量，求：（1)此质点在某一时刻的速率（2)法向 加速度和切向加速度的大小：(3)总加速度. 解：(1)o= (5bt2)=bt dtdt 2 dv (2) at= =b (b)2 an (3)a=(ai+a2)v2be +1)V2 coso t

1 – 3 圆周运动 例1设有一个质点作半径为 r 的圆周运动.质点沿 圆周运动所经历的路程与时间的关系为s = bt2 /2,并设b 为一常量,求:（1）此质点在某一时刻的速率;（2）法向 加速度和切向加速度的大小;（3）总加速度. 解:（1） bt bt t t = = ) = 2 1 ( d d d ds 2 v r bt r a 2 2 v ( ) （2） b n = = t a = = d d t v （3） 1 2 2 2 4 2 1 2 n 2 t = ( + ) = ( +1) r b t a a a b 1 2 2 2 4 t cos ( 1) − = = + r b t a a 