
§3-2 流体力学简介 流体:液体和气体 流体特征: 具有流动性; 没有固定的形状。 流体力学是研究流体的宏观运动规律的学科
§3-2 流体力学简介 流体:液体和气体 具有流动性; 没有固定的形状。 流体特征: 流体力学是研究流体的宏观运动规律的学科
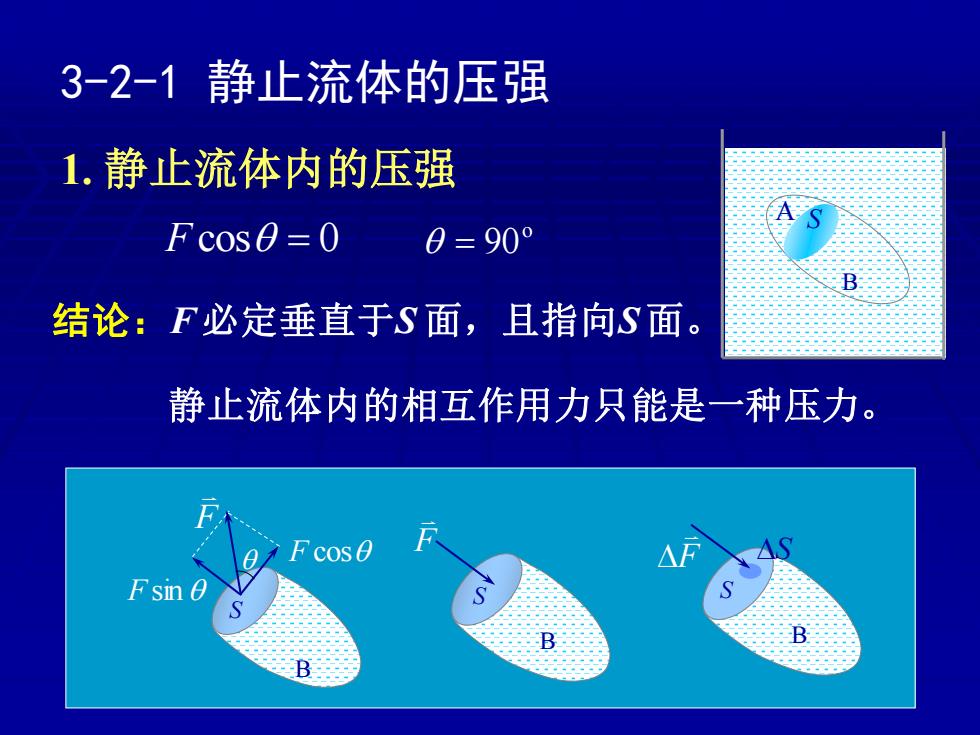
3-2-1静止流体的压强 1.静止流体内的压强 Fcos=0 0=90° 结论:F必定垂直于S面,且指向S面。 静止流体内的相互作用力只能是一种压力。 Fsin 0
3-2-1 静止流体的压强 1. 静止流体内的压强 B A S B F cos F sin S F B S F B S F S F cos = 0 o = 90 结论:F 必定垂直于S 面,且指向S 面。 静止流体内的相互作用力只能是一种压力

F 流体压强: P-AS 实验与理论证明: 某一点处的压强大小只取决于该点的位置,而 与压强的作用面的取向无关。 压强的单位: 帕斯卡(Pa) 1Pa=1N.m-2 不推荐使用的压强单位: 标准大气压(atm) 1atm=1.013×10sPa
S F p S = → lim 0 流体压强: 某一点处的压强大小只取决于该点的位置,而 与压强的作用面的取向无关 。 实验与理论证明: 压强的单位: 帕斯卡( Pa ) 1Pa=1N·m-2 1atm=1.013×105 Pa 不推荐使用的压强单位: 标准大气压(atm)
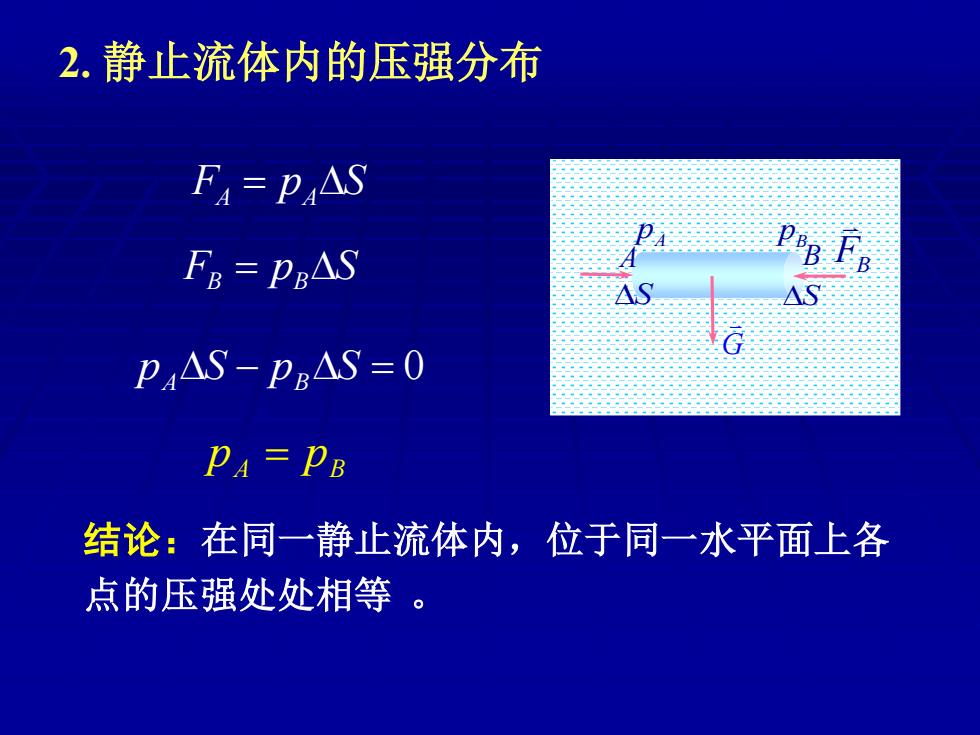
2.静止流体内的压强分布 FA=PAAS FB=PEAS PAAS-PBAS=0 PA=PB 结论:在同一静止流体内,位于同一水平面上各 点的压强处处相等
2. 静止流体内的压强分布 FA F p S A = A FB = pB S pA S − pB S = 0 pA = pB 结论:在同一静止流体内,位于同一水平面上各 点的压强处处相等 。 pA pB A B S S FB G

设流体的密度p为恒量 上端压力Fc=pcAS 下端压力F)=PnAS 重力 G=(h△S)p8 PDAS-PCAS-hASpg=0 PD-Pc pgh 结论:在同一种静止流体内,高度差为的任何两点 之间的压强差皆等于pgh
S C D pD C p FC G FD h 设流体的密度ρ为恒量 F p S 上端压力 C = C 下端压力 FD = pD S 重力 G = (hS)g pD S − pC S − hSg = 0 pD − pC = gh 结论:在同一种静止流体内,高度差为h的任何两点 之间的压强差皆等于ρgh

设静止液体自由表面上的环境压强为大气压强Pa p=Pa pgh 绝对压强:p 相对压强:p-Pa=P8h (计示压强) 真空度:p。-p(p<p)
设静止液体自由表面上的环境压强为大气压强 pa p = pa + gh h pa p 绝对压强: p 相对压强: p − pa = gh (计示压强) 真空度: pa − p ( ) p pa

3.静止流体内压强公式的物理意义 液体中A点的压强: p=Pamb +pg(H-2) pamb 卫+z=Pa+H pg pg H p为液体的密度 Pamb为环境压强 Pm+H=恒量 +z=恒量 pg p8
3. 静止流体内压强公式的物理意义 + z = 恒量 g p 液体中A点的压强: ( ) amb p = p + g H − z ρ为液体的密度 pamb为环境压强 + H = p g amb 恒量 H g p z g p + = + amb

对于液体中的任意两点,有 2+= 2十z2 p8 pamb 质元重力势能:△mg2 pg 单位重量质元的重力势能:z 单位重量的液体质元获得的 重力势能: 结论:静止液体内任一点的单 压力势能h。 位重量流体的重力势能和压力 8 势能之代数和为一恒量
对于液体中的任意两点,有 2 2 1 1 z g p z g p + = + 质元重力势能: mgz 单位重量质元的重力势能:z 单位重量的液体质元获得的 重力势能: 结论:静止液体内任一点的单 位重量流体的重力势能和压力 势能之代数和为一恒量。 g p hp 压力势能 =
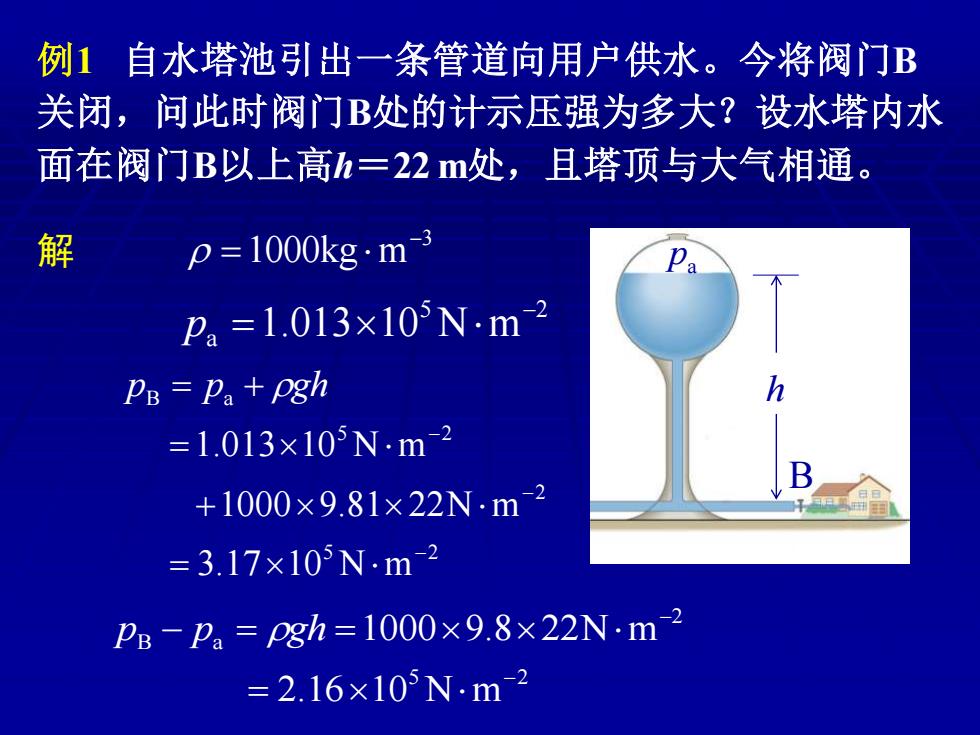
例1自水塔池引出一条管道向用户供水。今将阀门B 关闭,问此时阀门B处的计示压强为多大?设水塔内水 面在阀门B以上高h=22m处,且塔顶与大气相通。 解 p=1000kg·m3 pa=1.013×105N-m2 Pe Pa+pgh =1.013×105Nm2 +1000×9.81×22Nm-2 =3.17×105N.m2 pB-pa=Pgh=1000×9.8×22N,m2 =2.16×105N-m2
例1 自水塔池引出一条管道向用户供水。今将阀门B 关闭,问此时阀门B处的计示压强为多大?设水塔内水 面在阀门B以上高h=22 m处,且塔顶与大气相通。 解 3 1000kg m − = h B pa 5 2 a 1.013 10 N m − p = 5 2 2 5 2 B a 3.17 10 N m 1000 9.81 22N m 1.013 10 N m − − − = + = p = p + gh 5 2 2 B a 2.16 10 N m 1000 9.8 22N m − − = p − p = gh =

3-2-2 理想流体 理想流体的连续性方程 1.理想流体 理想流体:不可压缩、又没有粘性的流体。 理想流体的密度为恒量;在流动时各相邻流层之 间就不存在相互作用的切向力(内摩擦力)。 动压强:运动的理想流体内部的压强。 动压强与静止的实际流体内的压强(即静压强) 具有相同的性质,其内部某一点的压强沿各方向都 是相等的
3-2-2 理想流体 理想流体的连续性方程 1. 理想流体 理想流体:不可压缩、又没有粘性的流体。 理想流体的密度ρ为恒量;在流动时各相邻流层之 间就不存在相互作用的切向力(内摩擦力)。 动压强与静止的实际流体内的压强(即静压强) 具有相同的性质,其内部某一点的压强沿各方向都 是相等的。 动压强: 运动的理想流体内部的压强