
*2-5力学相对性原理非惯性系与惯性力 力学相对性原理 u ⑦=⑦'+⑦ 玩为常量 .∴.a=a' F=ma F=ma 结论 (1)凡相对于惯性系作匀速直线运动的一切参考 系都是惯性系· (2)对于不同惯性系,牛顿力学的规律都具有相 同的形式,与惯性系的运动无关 伽利略相对性原理
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 一 力学相对性原理 u v v' (2)对于不同惯性系,牛顿力学的规律都具有相 同的形式,与惯性系的运动无关 . (1)凡相对于惯性系作匀速直线运动的一切参考 系都是惯性系 . 伽利略相对性原理 x ut x x' y y' z z' O O u x' P 结论 a a' u 为常量 F ma F ma
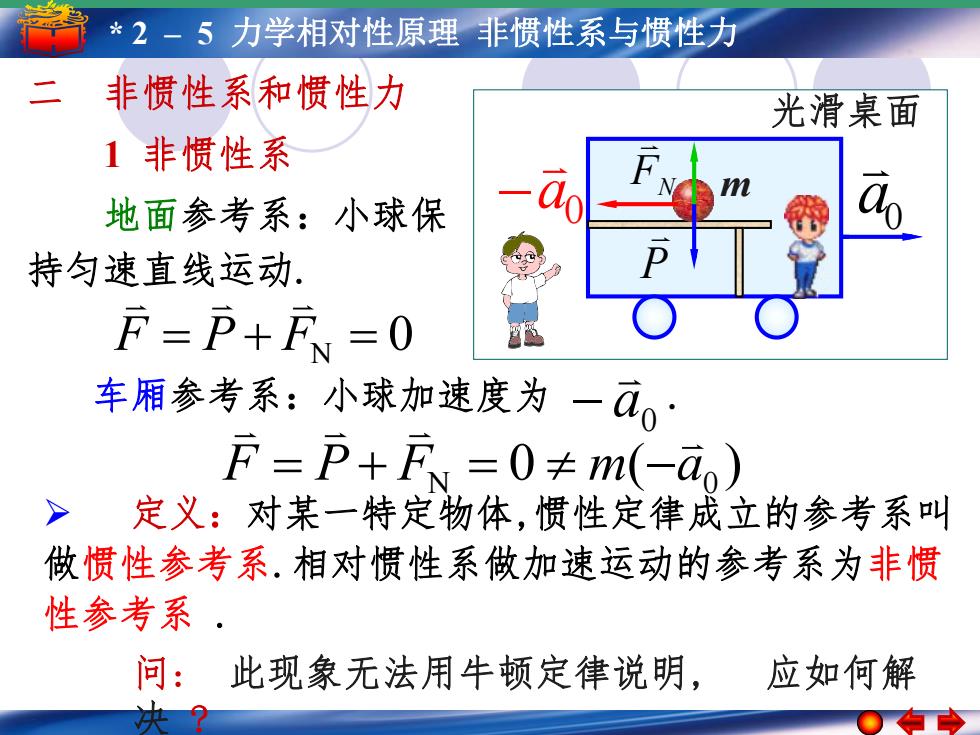
*2-5力学相对性原理非惯性系与惯性力 二非惯性系和惯性力 光滑桌面 1非惯性系 地面参考系:小球保 持匀速直线运动 F=P+FN=0 车厢参考系:小球加速度为一a0: F=p+F,=0≠m(-ao) >定义:对某一特定物体,惯性定律成立的参考系叫 做惯性参考系.相对惯性系做加速运动的参考系为非惯 性参考系。 问:此现象无法用牛顿定律说明, 应如何解
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 m 二 非惯性系和惯性力 光滑桌面 地面参考系:小球保 持匀速直线运动. F P FN 0 0 ( ) F P FN m a0 Ø 定义:对某一特定物体,惯性定律成立的参考系叫 做惯性参考系.相对惯性系做加速运动的参考系为非惯 性参考系 . 车厢参考系:小球加速度为 . 0 a P FN v 1 非惯性系 a0 0 a 问: 此现象无法用牛顿定律说明, 应如何解 决 ?
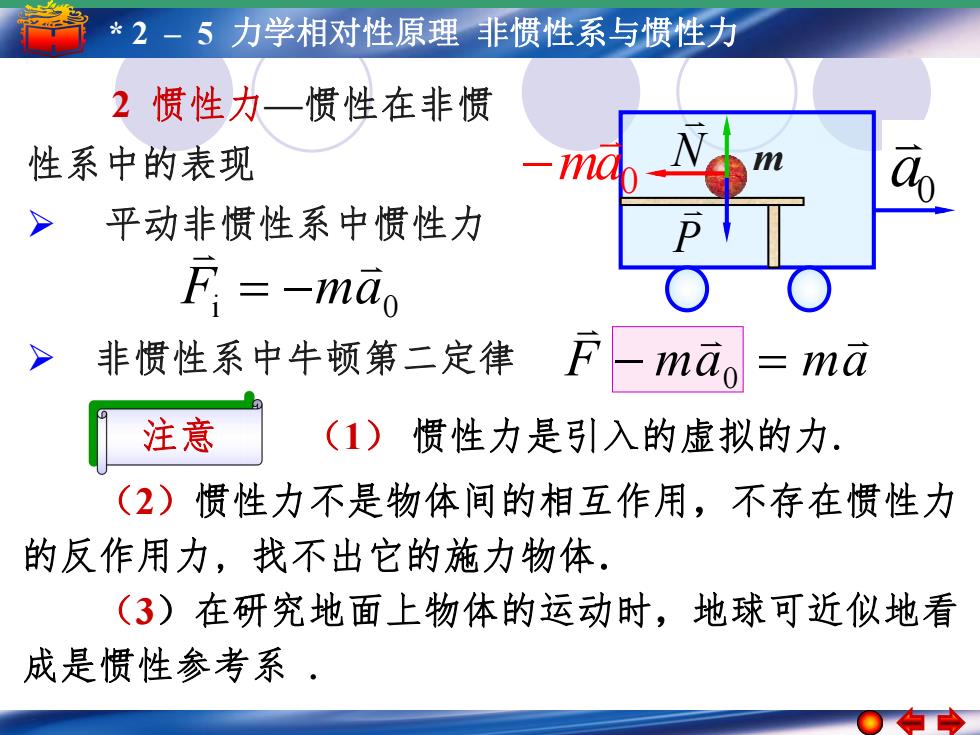
*2-5力学相对性原理非惯性系与惯性力 2惯性力一惯性在非惯 性系中的表现 > 平动非惯性系中惯性力 F:=-mao > 非惯性系中牛顿第二定律 -mao ma 注意 (1)惯性力是引入的虚拟的力. (2)惯性力不是物体间的相互作用,不存在惯性力 的反作用力,找不出它的施力物体. (3)在研究地面上物体的运动时,地球可近似地看 成是惯性参考系·
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 2 惯性力—惯性在非惯 性系中的表现 Ø 非惯性系中牛顿第二定律 F ma ma 0 (2)惯性力不是物体间的相互作用,不存在惯性力 的反作用力, 找不出它的施力物体. (3)在研究地面上物体的运动时,地球可近似地看 成是惯性参考系 . 注意 (1) 惯性力是引入的虚拟的力. i 0 F ma Ø 平动非惯性系中惯性力 m a0 0 ma P N

*2-5力学相对性原理非惯性系与惯性力 例1动力摆可用来测定车辆的加速度.一根质量不 计的细棒一端固定在车厢的顶部,另一端系一小球,当 列车以加速度行驶时,细杆偏离竖直线成心角.试求 加速度a与摆角间a的关系 解:以车厢为参考系(非惯性系)小球处于平衡状态, mg +F+F=0 分量式 F cosa-mg=0 a E sina-ma=0 解得a=g tan a≈g0
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 解: 以车厢为参考系(非惯性系)小球处于平衡状态. mg FT Fi 0 分量式 FT cos mg 0 sin 0 FT ma 解得 a g tan g Fi a FT P 例1 动力摆可用来测定车辆的加速度.一根质量不 计的细棒一端固定在车厢的顶部,另一端系一小球,当 列车以加速度 a 行驶时,细杆偏离竖直线成 角. 试求 加速度 a 与摆角间 的关系 .
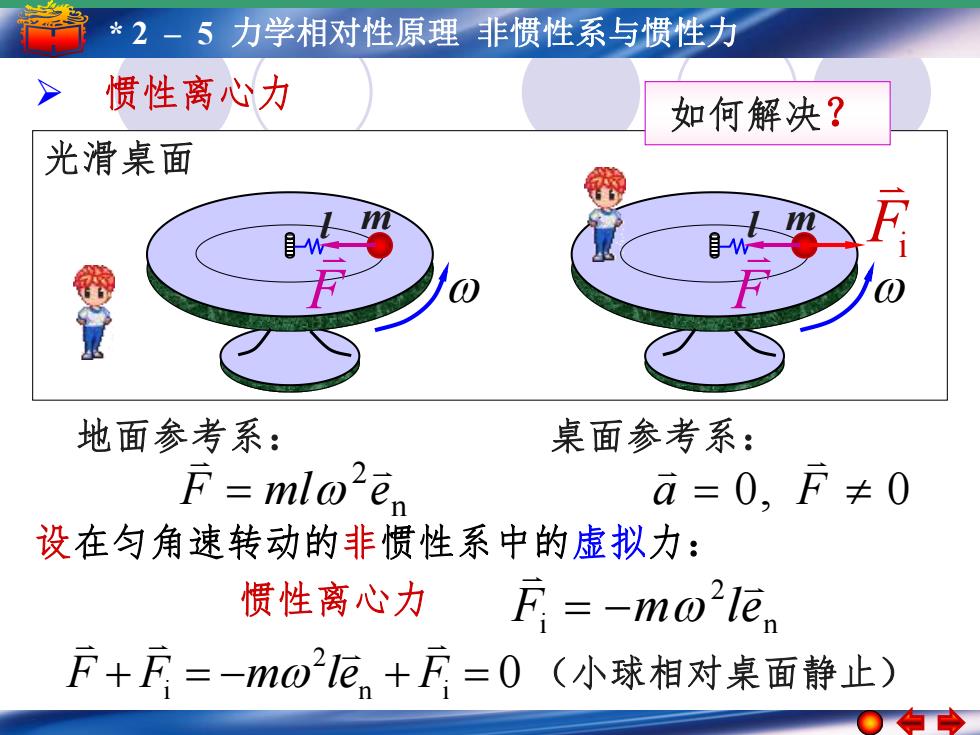
*2-5力学相对性原理非惯性系与惯性力 惯性离心力 如何解决? 光滑桌面 地面参考系: 桌面参考系: F=mlo-en a=0,F≠0 设在匀角速转动的非惯性系中的虚拟力: 惯性离心力 F =-mo'le, F+F=-mo2厄n+F=0(小球相对桌面静止)
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 光滑桌面 Ø 惯性离心力 m Fi l m F F 地面参考系: n 2 F ml e 桌面参考系: a 0, F 0 设在匀角速转动的非惯性系中的虚拟力: 惯性离心力 n 2 i F m le 0 n i 2 F Fi m le F (小球相对桌面静止) 如何解决? l

*2-5力学相对性原理非惯性系与惯性力 例2由于地球的自转, 故物体在地球表面所受的 重力与物体所处的纬度有关,试找出他们之间的关系. 解:在地面纬度日处,物体的重 力P(视重)等于地球引力与自转效 应的惯性离心力之矢量合,即 P=mg+F R F=mo'r=mo2Rcos0 P≈mg-Fcos0 =mg(1-@R cos20/g)=mg(1- os-0 物体的重力P在两极最大,在赤道最小 289
5* –21– 简5谐 力运学动相 简对谐性运原动理的 振非幅惯 性周期系 与频惯率性和力相位 例2 由于地球的自转, 故物体在地球表面所受的 重力与物体所处的纬度有关, 试找出他们之间的关系. P mg Fi cos 2 2 Fi m r m R P mg Fi cos ) 289 cos (1 2 mg 物体的重力 P 在两极最大, 在赤道最小. R r Fi mg O O (1 cos ) 2 2 mg R g P 解:在地面纬度 处 ,物体的重 力P(视重)等于地球引力与自转效 应的惯性离心力之矢量合,即