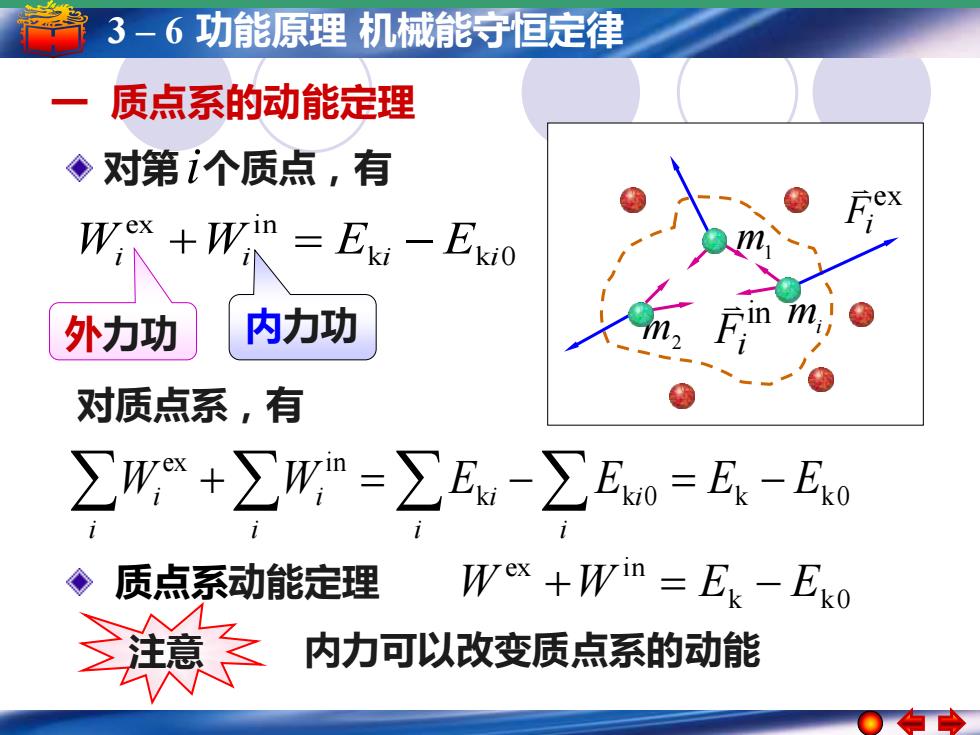
3-6功能原理机械能守恒定律 质点系的动能定理 ◆对第个质点,有 Wex +Wrin =Ek-Ekio 外力功 内力功 对质点系,有 ∑W+∑=∑E-∑Ew=E-Ew ◆质点系动能定理 Wex +win =Ek-Eko 柔 内力可以改变质点系的动能
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 一 质点系的动能定理 质点系动能定理 k k0 ex i n W +W = E − E m1 m2 mi ex Fi in Fi 注意 内力可以改变质点系的动能 k k 0 k k0 ex i n W W E E E E i i i i i i i i + = − = − 对质点系,有 k k 0 ex i n Wi +Wi = E i − E i 对第 i 个质点,有 外力功 内力功

3-6功能原理机械能守恒定律 二质点系的功能原理 质点系动能定理 wex+win =Ek-Es Wn=∑Wn=Wg+W8 非保守 力的功 W"=-(∑E-∑Eo)=-(E,-Eo) Wx+W=(E+E)-(Eko+E0) 机械能E=Ek+E, Wex +Wne =E-Eo 质点系的功能原理:质点系机械能的增量等于 外力和非保守内力作功之和
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 ( ) ( ) k p k0 p0 i n nc ex W +W = E + E − E + E 机械能 E = Ek + Ep 质点系动能定理 k k0 ex i n W +W = E − E 非保守 力的功 i n nc i n c i n i n W W W W i = i = + ( ) ( ) p p 0 p p0 in Wc E E E E i i i = − i − = − − 0 i n nc ex W +W = E − E 二 质点系的功能原理 质点系的功能原理:质点系机械能的增量等于 外力和非保守内力作功之和

3-6功能原理机械能守恒定律 三 机械能守恒定律 功能原理Wx+WC=(E+E,)-(Ek0+E0) 当Wex+Wn=0 nc 时,有E=E。 机械能守恒定律:只有保守内力作功的情况下,质 点系的机械能保持不变· Ek-Ek0=-(E。-E0) △Ek=-△E。 守恒定律的意义 不究过程细节而能对系统的状态下结论,这是各 个守恒定律的特点和优点
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 Ek = −Ep ( ) Ek − Ek0 = − Ep − Ep0 当 0 in nc ex W +W = 时,有 E = E0 ( ) ( ) k p k0 p0 i n nc ex 功能原理 W +W = E + E − E + E 三 机械能守恒定律 机械能守恒定律:只有保守内力作功的情况下,质 点系的机械能保持不变 . 守恒定律的意义 不究过程细节而能对系统的状态下结论,这是各 个守恒定律的特点和优点

3-6功能原理机械能守恒定律 讨论 如图所示的系统,物体A、B置于光滑的桌面上, 物体A和C,B和D之间摩擦因数均不为零,首先用 外力沿水平方向相向推压A和B,使弹簧压缩,后拆 除外力,则A和B弹开过程中,对A、B、C、D组成 的系统 (A)动量守恒,机械能守恒 (B)动量不守恒,机械能守恒 (C)动量不守恒,机械能不守恒 (D)动量守恒,机械能不一定守恒 D M B WWWWM B
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 如图所示的系统, 物体 A、B 置于光滑的桌面上, 物体 A 和 C, B和 D 之间摩擦因数均不为零, 首先用 外力沿水平方向相向推压 A 和 B,使弹簧压缩,后拆 除外力,则 A 和 B 弹开过程中,对 A、B、C、D 组成 的系统 讨论 (A)动量守恒,机械能守恒 (B)动量不守恒,机械能守恒 (C)动量不守恒,机械能不守恒 (D)动量守恒,机械能不一定守恒 D B C A D B C A

3-6功能原理机械能守恒定律 讨论 下列各物理量中,与参照系有关的物 理量是哪些? (不考虑相对论效应) (1)质量 (2)动量 (3)冲量 (4)动能 (5)势能 (6) 功 答:动量、动能、功
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 下列各物理量中,与参照系有关的物 理量是哪些? (不考虑相对论效应) (1)质量 (2) 动量 (3) 冲量 (4) 动能 (5) 势能 (6) 功 答:动量、动能、功 . 讨 论

3-6功能原理机械能守恒定律 例1已知地球的半径为Rε≈6.4×103km,今有质量为 m=3.0×103kg的人造地球卫星从半径为2RE的圆形轨 道上,经如图所示的半椭圆形轨道上的点变轨至半径为 4RE的另一个圆形轨道点b上.点α和点b处的椭圆轨道 与圆轨道的切线相切. 试问:卫星完成了变轨过程后获 得了多少能量? 解:由牛顿第二定律和万有 b 引力定律 2 G mem (2RE)2 2RE
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 解: 由牛顿第二定律和万有 引力定律 E 2 2 E E (2 ) 2R m R m m G va = a v b v RE 4RE a b o 例1 已知地球的半径为 RE ≈ 6.4×103 km,今有质量为 m = 3.0×103 kg 的人造地球卫星从半径为 2 RE 的圆形轨 道上,经如图所示的半椭圆形轨道上的点 a 变轨至半径为 4RE 的另一个圆形轨道点 b上.点 a 和点 b 处的椭圆轨道 与圆轨道的切线相切. 试问: 卫星完成了变轨过程后获 得了多少能量 ?

3 3-6功能原理机械能守恒定律 已知:RE≈6.4×103km,m=3.0×103kg mem G (2RE)2 =m 2RE G mE/RE=g a ∴.0。=(gRε/2)12 同理6=(gR:/4)1V2 4RE 00 Ea m2-Gm 1 1 a 2 E =-mgRe 4 AE=。mgK 1 Ep mem 1 8 -mt -G -。mgRz 4RE 8 =2.35x1010J
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 E E 2 E 4 1 2 2 1 mgR R m m Ea = mva −G = − 已知:RE ≈ 6.4×103 km, m = 3.0×103 kg E 2 2 E E (2 ) 2R m R m m G va = E E 2 E 8 1 2 4 1 mgR R m m Eb = mvb −G = − E 8 1 E = mgRJ 10 = 2.3510 G m RE = g 2 E 1/ 2 E = (gR / 2) va 1/ 2 E = (gR / 4) 同理 vb a v b v RE 4RE a b o

3-6功能原理机械能守恒定律 *四宇宙速度 牛顿的《自然哲学的数学原理》插图,抛体的运轨 迹取决于抛体的初速度
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 * 四 宇宙速度 牛顿的《自然哲学的数学原理》插图,抛体的运轨 迹取决于抛体的初速度

3-6功能原理机械能守恒定律 (1)人造地球卫星 第一宇宙速度 第一宇宙速度)1,是在地面上发射人造地球卫星所 需的最小速度 设:地球质量mE,抛体质量m,地球半径RE 解取抛体和地球为一系统, 系统的机械能E守恒. E +6 2 1 mx2+(-G me) 2 Re +h
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 设:地球质量 mE , 抛体质量 m ,地球半径 RE v h `````` 解: 取抛体和地球为一系统 , 系统的机械能 E 守恒 . (1) 人造地球卫星 第一宇宙速度 第一宇宙速度v1,是在地面上发射人造地球卫星所 需的最小速度 . ( ) 2 1 E 2 E 1 R mm E = mv + −G ( ) 2 1 E 2 E R h m m m G + = v + −

3-6功能原理机械能守恒定律 -m+(-G")-m24(- mme RE 2 Rε+h 由牛顿第二定律和万有引力定律得 ò2 mme m G Re +h (Rε+h)2 解得V1= 2GmE GmE RE Re+h :g=Gme/R陷 0=gRe(2- RE) Re +h 地球表面附近R王>h 故01=VgRE 计算得第一宇宙速度v,=7.9×103m/s
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 解得 R h Gm R Gm + = − E E E E 1 2 v v h `````` ( ) 2 1 ( ) 2 1 E 2 E E 2 E 1 R h m m m G R m m E m G + = v + − = v + − 2 E E E 2 (R h) mm G R h m + = + v 由牛顿第二定律和万有引力定律得 2 g = GmE RE (2 ) E E 1 E R h R gR + v = − 地球表面附近 RE h 故 v1 = gRE 7.9 10 m/s 3 计算得第一宇宙速度 v1 =