
5-4一维简谐运动的合成拍现象 两个同方向同频率简谐运动的合成 x1=A cos(ot+) x,=A,cos(ot+2) x=X+X2 A x=Acos(@t+p) X2 XX A=A+A+2AA2c0s(p2-01) A sin p+4 sin 2 两个同方向同频 tan⑩= 率简谐运动合成 4 coso+42 cos 后仍为简谐运动
5 – 4 一维简谐运动的合成 拍现象 1 A1 1 O x x 一 两个同方向同频率简谐运动的合成 1 2 x = x + x 1 1 2 2 1 1 2 2 cos cos sin sin tan A A A A + + = 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − x = Acos(t +) cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t A x2 x A2 2 两个同方向同频 率简谐运动合成 后仍为简谐运动
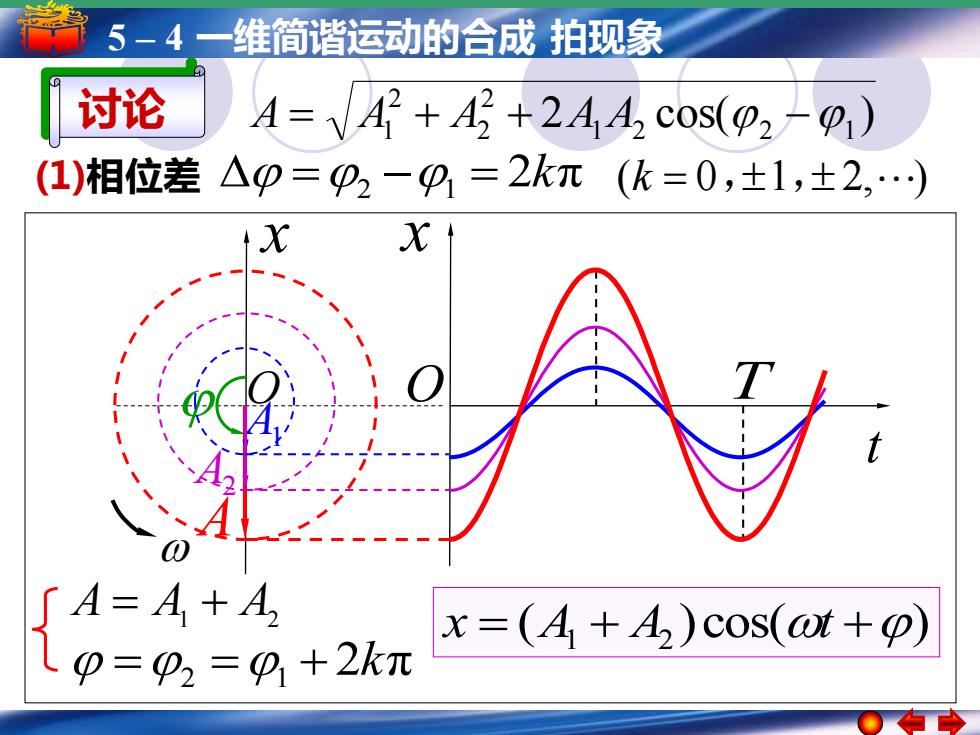
5-4 维简谐运动的合成拍现象 讨论 A=2+42+244 cos(p2-) (1)相位差△0=92-9=2k元(k=0,土士1,±2,) X X ∫A=A+A x=(4+4)cos(at+o) P=p2=9+2kπ
5 – 4 一维简谐运动的合成 拍现象 x x t O O =2 =1 + 2kπ ( )cos( ) x = A1 + A2 t + A A = A1 + A2 A1 A2 T (1)相位差 =2 −1 = 2kπ (k = 0,1, 2, ) 2 cos( ) 1 2 2 1 2 2 2 讨论 A = A1 + A + A A −
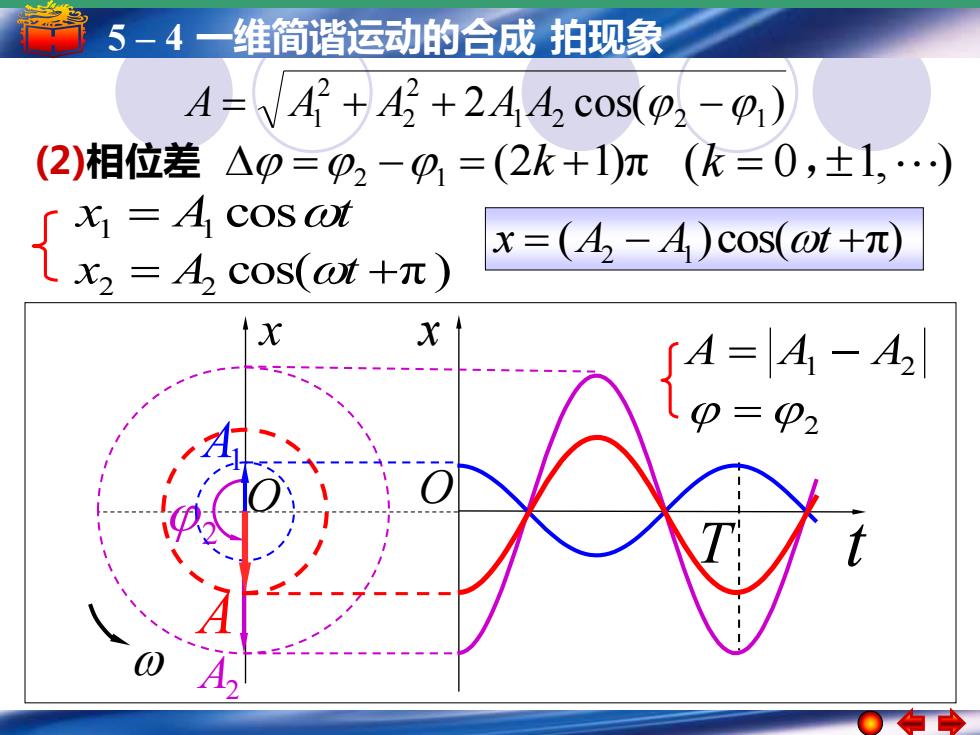
5-4一维简谐运动的合成拍现象 A=42+42+244 cos(o2-) (2)相位差△0=02-0,=(2k+1)m(k=0,±1,.) W三AcOs0 x=(A,-A)c0s(ot+π) x2=A2cos(t+π) tx X 「A=A-A2 、0=p2
5 – 4 一维简谐运动的合成 拍现象 x x t O O A = A1 − A2 = 2 ( )cos( π) x = A2 − A1 t + 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − T A2 2 A1 A (2)相位差 =2 −1 = (2k +1)π (k = 0,1, ) x A cost 1 = 1 cos( π ) x2 = A2 t +

5-4一维简谐运动的合成拍现象 4=42+42+244 cos(o2-) 相位差 △p=p2-P1 (1)相位差 △0=2k元 (k=0,±1,.) A=A十A 相互加强 (2)相位差 △p=(2k+1)π(k=0,±1,) A=4-4 相互减弱 (3)一般情况 A+A2>A>4-A2
5 – 4 一维简谐运动的合成 拍现象 (3)一般情况 A1 + A2 A A1 − A2 A = A1 − A2 (2)相位差 (1)相位差 A = A1 + A2 = 2k π (k = 0,1,) 相互加强 相互减弱 = (2k +1) π (k = 0,1,) ➢ 相位差 =2 −1 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A −

5-4一维简谐运动的合成拍现象 例1已知两个同方向的简谐振动: x1=0.04c0s(10t+π/3), x2=0.03cos(10t+p) 则(1)x+为最大时,为p 2π+π/3 (2)X+为最小时, 为02m+4π/3
5 – 4 一维简谐运动的合成 拍现象 (2) x1 + 为最小时, x2 为_ 则(1) 为最大时, 为_ 1 2 x + x 2kπ + π /3 2kπ + 4π /3 例1 已知两个同方向的简谐振动: 0.04cos(10 π 3), x1 = t + 0.03cos(10 ) x2 = t +

5-4一维简谐运动的合成拍现象 例2一质点同时参与两个在同一直线上的简谐 振动,求合振动的振幅和初相位· x=(4×102m)cos(2st+π/6) x2=(3×102m)cos(2st-5π/6) A A X A1 元 Λ0=元A=1×102mp=p1= 6 x=(1×102m)cos(2st+/6)
5 – 4 一维简谐运动的合成 拍现象 例 2 一质点同时参与两个在同一直线上的简谐 振动,求合振动的振幅和初相位 . (4 10 m)cos(2 s π 6) 2 1 1 = + − − x t (3 10 m)cos(2 s 5π 6) 2 1 2 = − − − x t = π 1 10 m −2 A = 6 π =1 = (1 10 m)cos(2 s π 6) 2 1 = + − − x t A1 A2 1 2 x O A

5-4一维简谐运动的合成拍现象 *二多个同方向同频率简谐运动的合成 x=A cos(ot+e) x2 =A cos(@t+2) x=4,cos(at+e) x=X+x2+.+Xn X X =Acos(@t+o) 多个同方向同频率简谐运动合成仍为简谐运动
5 – 4 一维简谐运动的合成 拍现象 1 A1 x O * 二 多个同方向同频率简谐运动的合成 A2 2 A3 3 x = Acos(t +) n x = x + x ++ x 1 2 cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t cos( ) n n n x = A t + A 多个同方向同频率简谐运动合成仍为简谐运动

5-4一维简谐运动的合成拍现象 x=A cosot A x2=Acos(t+△p) x3=Acos(t+2△p) AA AA Ax ●●● A=ΣA=NA, xy=A coslot+(N-1)Ap] (1)△p=2k元 A4△0 懿 △ (k=0,±1,±2,) (2)N△p=2k'元 (k'≠kW,k'=±1,±2,) X W个矢量依次相接构 成一个闭合的多边形· A=0
5 – 4 一维简谐运动的合成 拍现象 A1 A2 A3 A4 O x A5 A A NA0 i = i = A x A cost 1 = 0 cos( ) x2 = A0 t + cos[ ( 1) ] xN = A0 t + N − cos( 2 ) x3 = A0 t + A1 A2 A3 A4 x O A5 A6 A = 0 (k' kN,k' = 1,2, ) (2) N = 2k'π (1) = 2kπ (k = 0,1,2, ) 个矢量依次相接构 成一个闭合的多边形 . N 讨 论

5-4一维简谐运动的合成拍现象 米 三 两个同方向不同频率简谐运动的合成拍现象 *AAAAAAAMAAAAAAAAA AAAAAAWA X 频率较大而频率之差很小的两个同方向简谐运动的 合成,其合振动的振幅时而加强时而减弱的现象叫拍
5 – 4 一维简谐运动的合成 拍现象 * 三 两个同方向不同频率简谐运动的合成 拍现象 频率较大而频率之差很小的两个同方向简谐运动的 合成,其合振动的振幅时而加强时而减弱的现象叫拍

5-4一维简谐运动的合成拍现象 x=A cos@t=4 cos2n vit x=x+x2 X2=Ac0so2t=Ac0s2πV2 讨论A=A,Y2-<的情况2 ◆方法一 x=x1+x2=A1c0S2元yt+A2C0S2元y21 x=(24cos2πYtc0s2元 V2+V1 2 2 振幅部分 合振动频率
5 – 4 一维简谐运动的合成 拍现象 振幅部分 合振动频率 x x x A t A t 1 2 1 1 2 2π 2 = + = cos2π + cos 讨论 A1 = A2 2 − 1 1 + 2 , 的情况 x A t t 2 ) cos 2π 2 (2 cos 2π 2 1 2 1 1 − + = x A t A t 1 1 1 1 2π 1 = cos = cos x A t A t 2 2 2 2 2π 2 = cos = cos 1 2 x = x + x 方法一