
3-7碰撞 碰撞:两物体相互接触时间极短而相互作用力较大 的相互作用. :Fex<Fn.∑p=C 完全弹性碰撞:两物体碰撞之后,它们的动能之 和不变. Eks=Ek+Ek2=C 非弹性碰撞:由于非保守力的作用,两物体碰撞 后,使机械能转换为热能、声能、化学能等其他形式 的能量. 完全非弹性碰撞:两物体碰撞后,以同一速度运动
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 完全非弹性碰撞: 两物体碰撞后,以同一速度运动 . F F p C i i = ex in 碰撞:两物体相互接触时间极短而相互作用力较大 的相互作用 . Ek = Ek1 + Ek2 =C 完全弹性碰撞:两物体碰撞之后,它们的动能之 和不变 . 非弹性碰撞:由于非保守力的作用,两物体碰撞 后,使机械能转换为热能、声能、化学能等其他形式 的能量
3-7碰撞 完全弹性碰撞 (五个小球质量全同)
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 完全弹性碰撞 (五个小球质量全同)
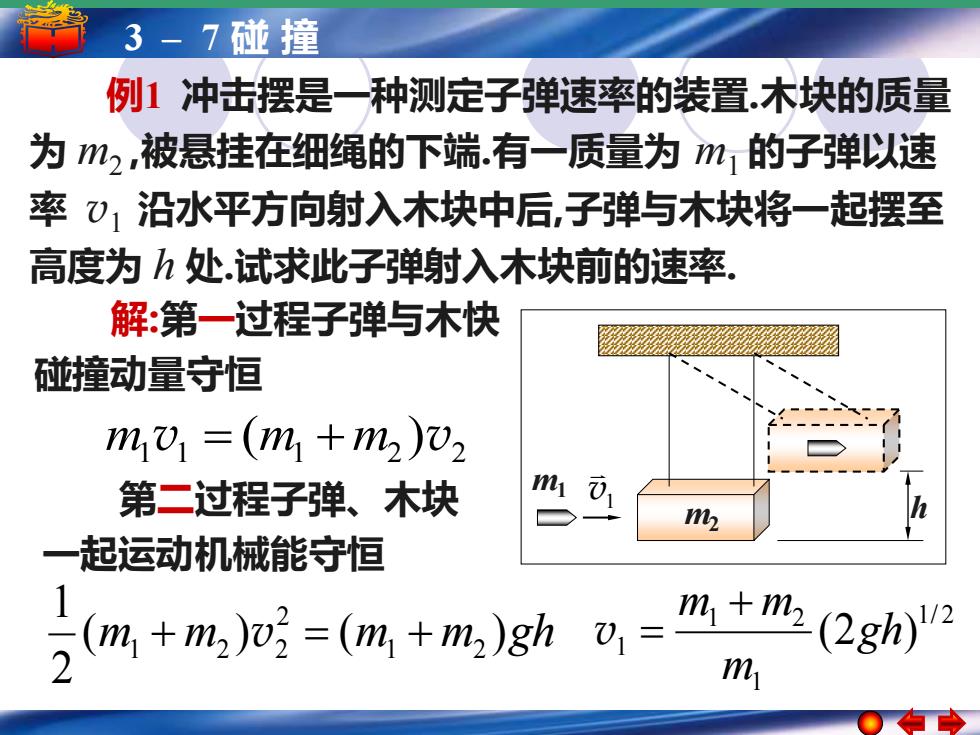
3-7碰撞 例1冲击摆是一种测定子弹速率的装置.木块的质量 为m2,被悬挂在细绳的下端.有一质量为m1的子弹以速 率)1沿水平方向射入木块中后,子弹与木块将一起摆至 高度为h处.试求此子弹射入木块前的速率. 解第一过程子弹与木快 碰撞动量守恒 m11=(m1+m2)w2 第二过程子弹、木块 2 一起运动机械能守恒 (m,+m2)o3=(m,+m2)gh01= (2gh)v2 2 m
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 m1 v1 m2 h 例1 冲击摆是一种测定子弹速率的装置.木块的质量 为 m2 ,被悬挂在细绳的下端.有一质量为 m1 的子弹以速 率 v1 沿水平方向射入木块中后,子弹与木块将一起摆至 高度为 h 处.试求此子弹射入木块前的速率. 解:第一过程子弹与木快 碰撞动量守恒 1 1 1 2 2 m v = (m +m )v (m m ) (m m )gh 2 1 1 2 2 1 + 2 v2 = + 1/ 2 1 1 2 1 (2gh) m m + m v = 第二过程子弹、木块 一起运动机械能守恒

3-7碰撞 例2设有两个质量分别为1,和m速度分别为 和可1的弹棰球作对心碰撞,两球的速度方向相同.若碰 撞是完全弹性的,求碰撞后的速度和 ō102 解:取速度方向为正向,由动 碰前 量守恒定律得 m2020 m1U10+1m2V20=m1U1+m2V2 A B m1(10-U1)=m2(02-020) 碰后 由机械能守恒定律得 m,+m.-m+m时 2 2 2 2
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 例 2 设有两个质量分别为 和 ,速度分别为 和 的弹性小球作对心碰撞,两球的速度方向相同. 若碰 撞是完全弹性的,求碰撞后的速度 和 . v20 m1 m2 v10 v1 v2 1 10 2 20 1 1 2 2 m v + m v = m v + m v 解:取速度方向为正向,由动 量守恒定律得 由机械能守恒定律得 2 2 2 2 1 1 2 2 2 0 2 1 1 0 2 1 2 1 2 1 2 1 m v + m v = m v + m v A m1 m2 v10 v20 B v1 v2 A B 碰前 碰后 ( ) ( ) 1 10 1 2 2 20 m v − v = m v − v
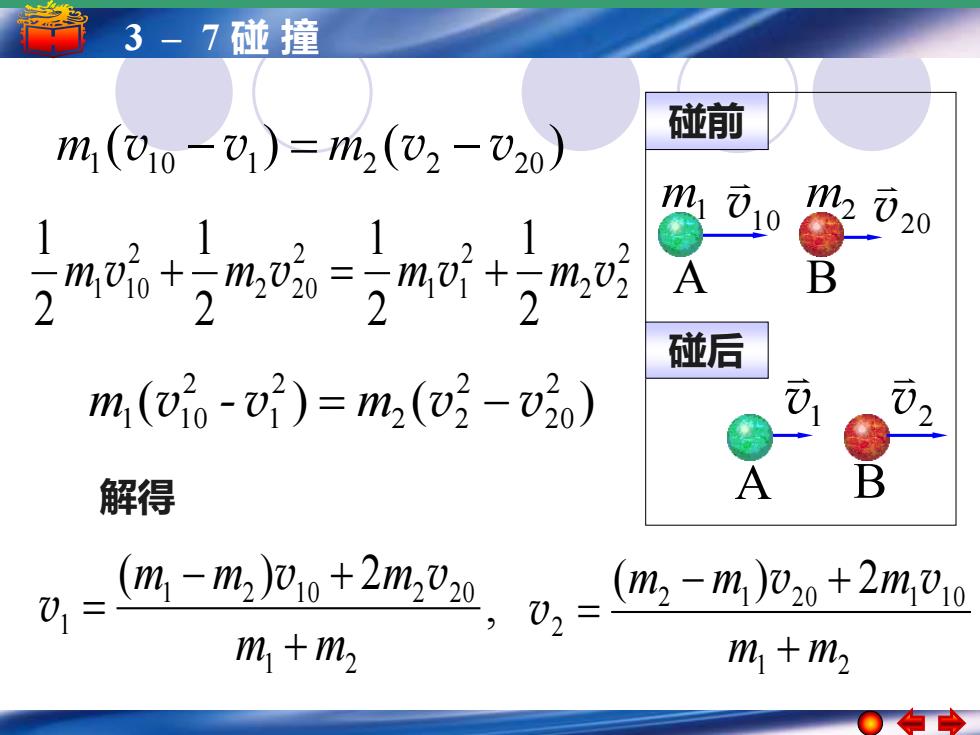
3-7碰撞 碰前 m(10-01)=m2(02-20 020 A B 碰后 m,(2。-0)=m(-3) 解得 B 0-m-m0+2m,0n 0= (m2-m,)020+2m,010 m1+m2 m1+m2
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 2 2 2 2 1 1 2 2 2 0 2 1 1 0 2 1 2 1 2 1 2 1 m v + m v = m v + m v ( ) ( ) 2 2 0 2 2 2 2 1 2 1 1 0 m v - v = m v − v ( ) ( ) 1 10 1 2 2 20 m v − v = m v − v 解得 , ( ) 2 1 2 1 2 1 0 2 2 0 1 m m m m m + − + = v v v 1 2 2 1 2 0 1 1 0 2 ( ) 2 m m m m m + − + = v v v A m1 m2 v10 v20 B v1 v2 A B 碰前 碰后

3-7碰撞 (m,-m2)v10+2m2V20 碰前 01= m1+m2 m m 10 ,020 A B (m2-m1)V20+2m,010 02= 碰后 m1+m2 讨论 (1)若m1=m2则01=020,V2=010 (2)若m2>m且020=0则)1≈-V10,02≈0 (3)若m3<m且V20=0则01≈010,2≈2V0
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 (1)若 m1 = m2 则 1 20 2 10 v = v , v = v (2)若 且 0 v20 = m2 m1 则 , 0 v1 −v10 v2 0 (3)若 m2 m1 且 v20 = 1 10 2 10 则 v v , v 2v 讨 论 1 2 1 2 1 0 2 2 0 1 ( ) 2 m m m m m + − + = v v v 1 2 2 1 2 0 1 1 0 2 ( ) 2 m m m m m + − + = v v v A m1 m2 10 v 20 v B v1 2 v A B 碰前 碰后

3-7碰撞 例3在宇宙中有密度为ρ的尘埃,这些尘埃相对惯性 参考系是静止的.有一质量为m的航天器以初速v,穿过 宇宙尘埃,由于尘埃粘贴到航天器上,致使航天器的速度发 生改变求航天器的速度与其在尘埃中飞行时间的关系, (设想航天器的外形是面积为S的圆柱体) 解:尘埃与航天器作完全非弹 性碰撞,则动量守恒mVo=mW dm movo dy pSodt 3 ro du 03- m)2
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 例3 在宇宙中有密度为 的尘埃,这些尘埃相对惯性 参考系是静止的.有一质量为 m0 的航天器以初速 v0 穿过 宇宙尘埃,由于尘埃粘贴到航天器上,致使航天器的速度发 生改变.求航天器的速度与其在尘埃中飞行时间的关系. (设想航天器的外形是面积为 S 的圆柱体) m v 解: 尘埃与航天器作完全非弹 性碰撞, 则动量守恒 . m0 v0 = mv v v v d d 2 m m0 0 = − = Svdt − = t t m S 0 0 0 3 d d 0 v v v v v 0 1 2 0 0 0 ) 2 ( v v v S t m m + =

3-7碰撞 1999年2月美国 发射的”星尘号 飞船收集彗星尘埃的 想象图
5 3 – 1–简谐运动 7 碰 撞简谐运动的振幅 周期 频率和相位 1999 年 2 月美国 发射的 “ 星尘号 ” 飞船收集彗星尘埃的 想象图