《大学物理》课程教学课件（PPT讲稿，高教版）牛顿定律习题课选讲例题

牛顿定律习题课选讲例题 例质量为m的物体自空中落下，它除受重力外， 还受到一个与速度平方成正比的阻力的作用.比例系数 为k，飞为正常数.该下落物体的终极速度（即最后物 体做匀速直线的速度)将是 mg (A) (B) 8 2k (C)gk (D) gk

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 例 质量为 m 的物体自空中落下,它除受重力外, 还受到一个与速度平方成正比的阻力的作用.比例系数 为 k ，k 为正常数.该下落物体的终极速度（即最后物 体做匀速直线的速度）将是 k mg (A) (C) gk k g 2 (B) (D) gk

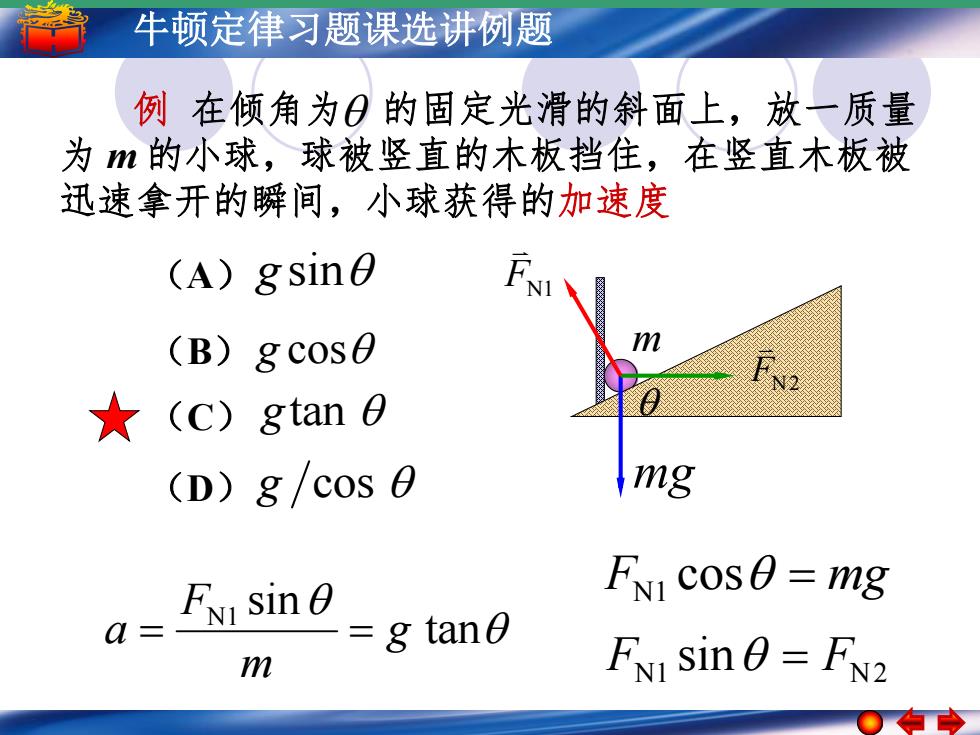
牛顿定律习题课选讲例题 例在倾角为日的固定光滑的斜面上，放一质量 为m的小球，球被竖直的木板挡住，在竖直木板被 迅速拿开的瞬间，小球获得的加速度 (A)gsine (B)gcose ★(c)8tan日 (D)g/cos 0 mg FN sin FN cos=mg a= g tan0 m FNI Sinθ=FN2

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 （A） （B） （C） g sin g cos （D）g cos  gtan   m mg FN1  FN2  FN1 cos  mg N1 N2 F sin  F   tan N1 sin g m F a   例 在倾角为 的固定光滑的斜面上，放一质量 为 m 的小球，球被竖直的木板挡住，在竖直木板被 迅速拿开的瞬间，小球获得的加速度 

牛顿定律习题课选讲例题 例一小环可在半径为R的大圆环上无摩擦地滑动， 大圆环以其竖直直径为轴转动，如图所示当圆环以恒定 角速度0转动，小环偏离圆环转轴而且相对圆环静止时， 小环所在处圆环半径偏离竖直方向的角度日为 (A)0=元/2 ☆(B)日=arccos(g/o2R) (c)0=arctan(o2R/g)(D)需由小环质量决定 解：对小环受力分析，有 N cos0 mg Nsin0=mo'Rsin 从以上二式可得到 cos0=_8 mg aPR

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 （A） （B） （C） （D）需由小环质量决定 N cos  mg sin  sin 2 N  m R R g 2 cos    解: 对小环受力分析，有 从以上二式可得到  mg  N  R 例 一小环可在半径为R 的大圆环上无摩擦地滑动, 大圆环以其竖直直径为轴转动,如图所示.当圆环以恒定 角速度 转动,小环偏离圆环转轴而且相对圆环静止时, 小环所在处圆环半径偏离竖直方向的角度 为     π 2 arccos( ) 2   g  R arctan( ) 2    R g

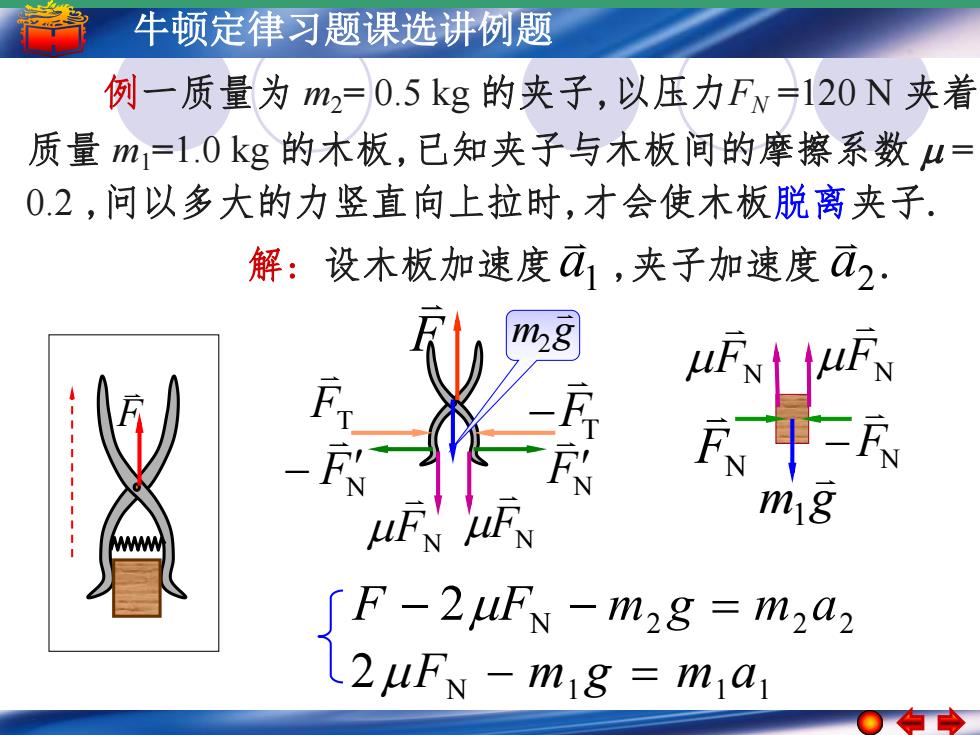
牛顿定律习题课选讲例题 例一质量为2=0.5kg的夹子，以压力Fv=120N夹着 质量m1=1.0kg的木板，已知夹子与木板间的摩擦系数μ= 02,问以多大的力竖直向上拉时，才会使木板脱离夹子 解：设木板加速度a1,夹子加速度a2: m28 F F年R mg WWWW ∫F-2uFN-m2g=m2a2 2uFy-mig mia

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 解: 设木板加速度 ,夹子加速度 . a1 a2 F  m g  2 FN   FN   m g  1 FN  FN   FN   FN   例一质量为 m2= 0.5 kg 的夹子,以压力FN =120 N 夹着 质量 m1=1.0 kg 的木板,已知夹子与木板间的摩擦系数  = 0.2 ,问以多大的力竖直向上拉时,才会使木板脱离夹子. N 2 2 2 F  2F  m g  m a 2FN  m1 g  m1a1 FN    FN   FT FT  F 

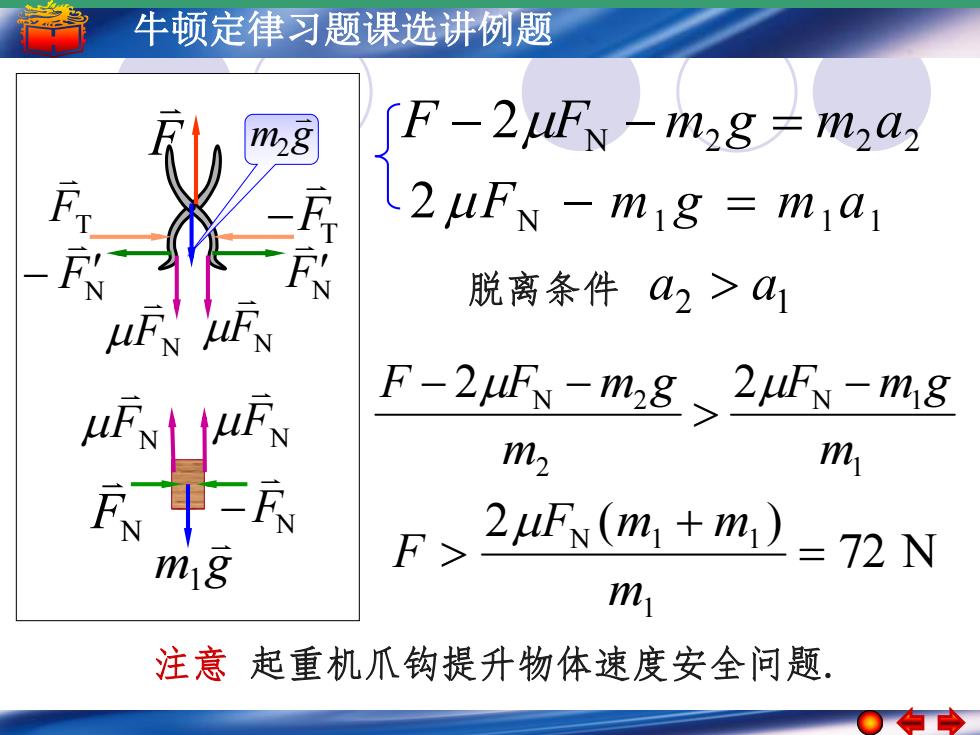
牛顿定律习题课选讲例题 m28 ∫F-2uF-m28=m2a2 2uFy -mig mia F 脱离条件a2>1 uF F-2F-m28、2uFN-m8 m2 m m18 F 2uF(m1+m）=72N m 注意起重机爪钩提升物体速度安全问题

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 1 N 1 2 N 2 2 2 m F m g m F F m g       72 N 2 ( ) 1 N 1 1    m F m m F  F  2FN  m2 g  m2a2 2FN  m1 g  m1a1 2 1 脱离条件 a  a 注意 起重机爪钩提升物体速度安全问题. FN   FN   m g  1 FN  FN   m g  2 FN   FN   FN    FN   FT FT  F 

牛顿定律习题课选讲例题 例一跳空运动员质量为80kg,一次从4000m高空 的飞机上跳出，以雄鹰展翅的姿势下落，有效横截面积为 0.6m2.以空气密度为1.2kgm3和阻力系数C=0.6计算，他 下落的终极速率多大？ 已知：fa=CpA2/2,C=0.6 22kgm4kcpM心em a=0,0=0 2mg 0L= mg

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 已知： mg  C A  ma 2 2 1 解：  v mg  d f y L a  0, v  v C A mg  2 vL  例 一跳空运动员质量为80 kg,一次从 4 000 m 高空 的飞机上跳出,以雄鹰展翅的姿势下落,有效横截面积为 0.6 m2.以空气密度为1.2 kg/m3 和阻力系数 C=0.6 计算,他 下落的终极速率多大？ 2, 0.6 2 fd  CAv C  3 2   1.2 kg/m , A  0.6 m

牛顿定律习题课选讲例题 例已知一物体质量m沿水平方向运动，初速度为 003 所受的阻力为F=一k),求停止运动时，物体运动 的距离。 解： dv F =-ko=ma=m dt dv dv dv -k)=m) dt dx dx k dv m 0 m x=-00 X= 00 m k

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 例 已知一物体质量 m 沿水平方向运动,初速度为 v0, 所受的阻力为 Ff=  k v，求停止运动时,物体运动 的距离. t Ff k ma m d dv   v   x v v v d d d d  t x v v v d d  k  m  dx  dv m k v 0 v0    d  d 0 x m k x   v0 x m k v0 k m x  解：

牛顿定律习题课选讲例题 例如图所示长为l的轻绳，一端系质量为m的小球， 另一端系于定点O,仁0时小球位于最低位置，并具有 水平速度0，求小球在任意位置的速率及绳的张力. 解：Fr-mg cos0=mC -mg sin 0 ma, FT-mg cos0=m2/1 dv -mg sin =m dt 7 mg dodo do d) dt de di =+21g(cos0-1) d sin Odm3 cos0)

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 t mg m d d sin v    解：        0 d sin d 0 gl v v v v ( 2 3 cos ) 2 0 T g g  l F  m   v    d d d d d d d dv v v v t t l   2 (cos 1) 2 v  v0  lg   t  mg sin   ma T n F  mg cos  ma F mg cos m / l 2 T    v 例 如图所示长为l 的轻绳，一端系质量为m的小球, 另一端系于定点O，t=0 时小球位于最低位置，并具有 水平速度v0，求小球在任意位置的速率及绳的张力. o  v 0 v  FT mg  t e n  e 

牛顿定律习题课选讲例题 例质量为m的物体在摩擦系数为u的平面上作匀 速直线运动，问当力与水平面成0角多大时最省力？ 解：建立坐标系， 受力分析，列受力方程 F cos 0-uN =0 F N+Fsin0-mg=0 联立求解：F= umg mg cos0+usinθ 分母有极大值时，F有极小值，y=c0sB+4SinB dy/dθ=0，dy/d0/2<0,8=arctan u

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位  F  例 质量为m的物体在摩擦系数为 的平面上作匀 速直线运动，问当力与水平面成  角多大时最省力？ 解：建立坐标系， 受力分析，列受力方程 . x y mg  Ff  FNO F cos   N  0 N  F sin  mg  0 联立求解：     cos  sin  mg F 分母有极大值时，F 有极小值，y  cos    sin  dy d  0, d d / 0,   arctan  2 2 y  

牛顿定律习题课选讲例题 例质量为m的物体，在F=F。-t的外力作用下 沿x轴运动，已知t=0时，x0=0,0=0,求：物体在 任意时刻的加速度a,速度v和位移x. F 解：a= =Fo-kt .do _F-kt dt m m dt m Fo二KLd Fot- m m 2m 由 dx )= 有 dx =odt dt 一 ydt X= k 2m 2m 6m

5 –牛1 顿简定谐运律动习 简题谐课运选动的讲振例幅题 周期 频率和相位 t m t F kt d d 0 0 0    v v 0 2 2 t m k t m F v   由 t x d d v  有 dx  vdt t t m k t m F x x t )d 2 d ( 0 0 2 0    0 2 3 2 6 t m k t m F x   例 质量为 m 的物体，在 F = F0kt 的外力作用下 沿 x 轴运动，已知 t = 0 时，x0= 0,v0= 0, 求：物体在 任意时刻的加速度 a，速度 v 和位移 x . 解： t m F kt d d 0   v  m F a  dt dv  m F  kt  0