
刚体的转动习题课选讲例题 例一人握有两只哑铃,站在一可无摩擦地转动的 水平平台上,开始时两手平握哑铃,人、哑铃、平台组 成的系统以一角速度旋转,后来此人将哑铃下垂于身 体两侧,在此过程中,系统 大(4)角动量守恒,机械能不守恒 (B)角动量守恒,机械能守恒 (C)角动量不守恒,机械能守恒 (D)角动量不守恒,机械能不守恒
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 例 一人握有两只哑铃,站在一可无摩擦地转动的 水平平台上,开始时两手平握哑铃,人、哑铃、平台组 成的系统以一角速度旋转,后来此人将哑铃下垂于身 体两侧,在此过程中,系统 (A) 角动量守恒, 机械能不守恒 (B) 角动量守恒, 机械能守恒 (C) 角动量不守恒, 机械能守恒 (D) 角动量不守恒, 机械能不守恒

刚体的转动习题课选讲例题 例关于力矩有以下几种说法: (1)内力矩不会改变刚体对某个轴的角动量; (2)作用力和反作用力对同一轴的力矩之和必为零: (3)质量相等,形状和大小不同的两个刚体,在相同 力矩的作用下,它们的角加速度一定相等: 在上述说法中 (A)只有(2)是正确的 ★(B)(1)、(2)是正确的 (C)(2)、(3)是正确的 (D)(1)、(2)、(3)都是正确的
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 例 关于力矩有以下几种说法: (1)内力矩不会改变刚体对某个轴的角动量; (2)作用力和反作用力对同一轴的力矩之和必为零; (3)质量相等, 形状和大小不同的两个刚体, 在相同 力矩的作用下, 它们的角加速度一定相等; 在上述说法中 (A) 只有(2)是正确的 (B)(1)、(2)是正确的 (C)(2)、(3)是正确的 (D)(1)、(2)、(3)都是正确的
刚体的转动习题课选讲例题 例如图所标,A、B为 两个相同的定滑轮,A滑轮 2 2 挂一质量为m的物体,B滑 轮受力F=mg,设A、B两 滑轮的角加速度分别为a4 7=m8 和aB,不计滑轮的摩擦,这 两个滑轮的角加速度 的大小关系为 (A)aA-aB ☆(c) aA<OB (B) (D)无法确定 mg B Fr=mgr=Jag =J mg -T=ma
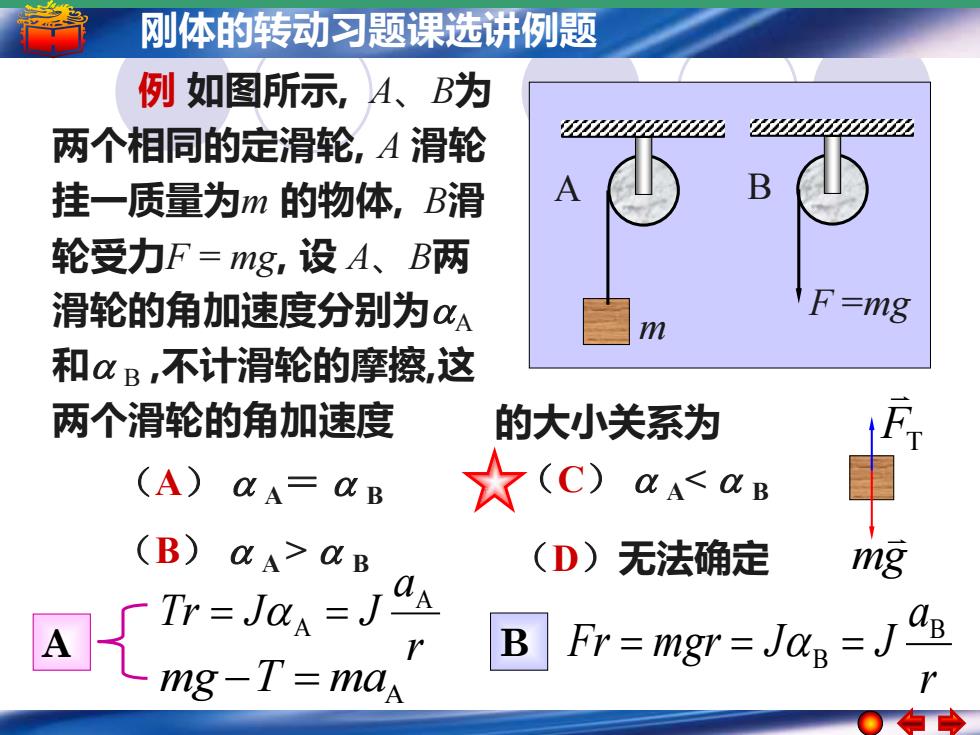
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 A m B F =mg (A) A= B (B) A > B (C) A< B (D)无法确定 例 如图所示, A、B为 两个相同的定滑轮, A 滑轮 挂一质量为m 的物体, B滑 轮受力F = mg, 设 A、B两 滑轮的角加速度分别为A 和 B ,不计滑轮的摩擦,这 两个滑轮的角加速度 的大小关系为 mg −T = maA r a Tr J J A = A = A r a Fr mgr J J B B = = B = mg FT

刚体的转动习题课选讲例题 例人造地球卫星绕地球作椭圆轨道运动,地球 在椭圆的一个焦点上,则卫星的: (A)动量不守恒,动能守恒 (B)动量守恒,动能不守恒 ★ (C)角动量守恒,动能不守恒 (D)角动量不守恒,动能守恒
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 (A) 动量不守恒, 动能守恒 (B) 动量守恒, 动能不守恒 (C) 角动量守恒, 动能不守恒 (D) 角动量不守恒, 动能守恒 例 人造地球卫星绕地球作椭圆轨道运动, 地球 在椭圆的一个焦点上, 则卫星的:

刚体的转动习题课选讲例题 例一飞轮在时间t内转过角度0=t+b3式a b、C都是常量,求它的角加速度 解 0= d (at+bi-cl)=a+3b12-4ct a-9(a+3br2-4ct)=6bt-12cr2 dt
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 例 一飞轮在时间t 内转过角度 ,式中 a、 b、c 都是常量,求它的角加速度. 3 4 = at + bt − ct 3 4 2 3 ( ) 3 4 d d at bt ct a bt ct t = + − = + − 2 3 2 ( 3 4 ) 6 12 d d a bt ct bt ct t = + − = − 解:

刚体的转动习题课选讲例题 例一条缆索绕过一定滑轮拉动一升降机,滑轮半径 r=0.5m,如果升降机从静止开始以a=0.4ms2加速度 上升,求:(1)滑轮角加速度;(2)t=5s时角速度 及转过的圈数;(3)t=1s时轮缘上一点的加速度. 已知:r=0.5m,a=0.4ms2 解:(1) a=a=0.4ms2 Ct」 a a= a 0.4 Q= 0.8(rad·s2) 0.5
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 解:(1) 0.8 (rad s ) 0.5 0.4 −2 = = r a r a = = t 例 一条缆索绕过一定滑轮拉动一升降机,滑轮半径 r = 0.5 m , 如果升降机从静止开始以 a = 0.4 m·s -2 加速度 上升, 求:(1)滑轮角加速度;(2)t = 5 s 时角速度 及转过的圈数;(3) t = 1 s 时轮缘上一点的加速度. 已知: r = 0.5 m, a = 0.4 m·s -2 a r 2 t 0.4 m s − a = a =

刚体的转动习题课选讲例题 求:(2)t=5s时角速度及转过的圈数: a=0.8rad.s-2 o=at=4rad.s- 0 0-Lat2-10rad 1 n= =1.6 2 2π 求(3)t=1s时轮缘上一点的加速度. r=0.5m a=a=0.4ms2 a ω=ot=0.8rad.sl a,=ro2 =0.32 m.s-2 a a'=a+a =0.51m-s2 B=arctan(an/a)=38.7
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 1 4 rad s − = t = 1.6 2π = = n 2 t 0.4 m s − a = a = 2 2 n 0.32 m s − a = r = 10 rad 2 1 2 = t = 1 0.8 rad s − =t = 求:(2) t = 5 s 时角速度及转过的圈数; 2 0.8rad s − = 求(3)t = 1 s 时轮缘上一点的加速度. r = 0.5 m 2 2 n 2 t 0.51m s − a = a + a = = arctan(an at ) = 38.7 a r n a at a

刚体的转动习题课选讲例题 例一长为,重为P的均匀梯子,靠墙放置,墙光 滑,当梯子与地面成0角时处于平衡状态,求梯子与 地面的摩擦力, 解:刚体平衡的条件 ∑F=0 ∑M=0 F-F2=0P-F1=0 以支点0为转动中心,梯子受 的合外力矩: Pcos0-Fl sin =0 F=FN2= P 。cot0 2
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 l O = 0 Fi Mi = 0 解: 刚体平衡的条件 例 一长为l,重为P 的均匀梯子,靠墙放置,墙光 滑,当梯子与地面成 角时处于平衡状态,求梯子与 地面的摩擦力. Ff − FN2 = 0 P − FN1 = 0 以支点O为转动中心,梯子受 的合外力矩: cos sin 0 2 − FN2 l = l P cot 2 f N2 P F = F = FN1 FN2 P Ff

刚体的转动习题课选讲例题 例一质量为m、长为L的均匀细棒,可在水平桌面上 绕通过其一端的竖直固定轴转动,已知细棒与桌面的摩 擦因数为4,求棒转动时受到的摩擦力矩的大小· 解:取一小段如图所示 n dx dm dF;udmg dM=x(udmg) M-jwng=xd=3mg2
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 x O 例 一质量为m、长为L的均匀细棒,可在水平桌面上 绕通过其一端的竖直固定轴转动,已知细棒与桌面的摩 擦因数为 , 求棒转动时受到的摩擦力矩的大小. x dx f dF 解: 取一小段如图所示 x l m dm = d dM = x(dmg) x x mgL l m g M x m g L 2 1 d d 0 = = = dFf = dmg

刚体的转动习题课选讲例题 例电风扇在开启电源后,经1时间达到了额定 转速,此时相应的角速度为,当关闭电源后,经 过t2时间风扇停转.已知风扇转子的转动惯量为J, 并假设摩擦阻力矩和电机的电磁力矩均为常量,求 电机的电磁力矩。 解 M-M=Ja M:=Ja M-m,+ ω0=Ct1=C2t2
5 –刚体的转动习题课选讲例题 1 简谐运动 简谐运动的振幅 周期 频率和相位 例 电风扇在开启电源后,经 t1时间达到了额定 转速,此时相应的角速度为0 ,当关闭电源后,经 过 t2 时间风扇停转.已知风扇转子的转动惯量为J, 并假设摩擦阻力矩和电机的电磁力矩均为常量,求 电机的电磁力矩. ) 1 1 ( 1 2 0 t t M = Jω + 解: 0 1 1 2 2 ω = t = t f 1 M − M = J f 2 M = J