
机械振动内容提要 简谐运动的描述和特征 (1)物体受线性恢复力作用F=-x平衡位置X=0 (2)简谐运动的动力学描述 d2x 2 =一0X dt2 (3)简谐运动的运动学描述 x=AcoS(⊙t+p) (在无外驱动力的情况下) =-Aosin(ot+o (4)加速度与位移成正比而方向相反a=-o2x (5) 三个特征量:振幅A决定于振动的能量: 角频率 决定振动系统的性质; 初相 决定牙起始时刻的选择
机械振动内容提要 x t x 2 2 2 d d (2) 简谐运动的动力学描述 = − v = −A sin(t +) x = Acos(t +) (3) 简谐运动的运动学描述 (在无外驱动力的情况下) 一 简谐运动的描述和特征 (5) 三个特征量:振幅 A 决定于振动的能量; 角频率 决定于振动系统的性质; 初相 决定于起始时刻的选择. a x 2 (4) 加速度与位移成正比而方向相反 = − (1) 物体受线性恢复力作用 F=-kx 平衡位置 x = 0

机械振动内容提要 实例:弹簧振子 w=k/m 单摆0三Vg/ 二相位 at+o (1)ωt+D>存在0对应的关系: (2)相位在0~变化,质点无相同的运动状态; 相差2m(为整数)质点运动状态全同(周期性). (3)初相位p(t=0)描述质点初始时刻的运动状态, (取[-元或元)[0→2元] (4) 对于两个同频率简谐运动相位差 △=p2-P1 简谐运动旋转矢量表示法 方法简单、直观,用于判断简谐运动的初相及相位, 分析振动的合成问题
机械振动内容提要 (4) 对于两个同频率简谐运动相位差 =2 −1 实例 : 弹簧振子 = k m 单摆 = g l 三 简谐运动旋转矢量表示法 方法简单、直观, 用于判断简谐运动的初相及相位, 分析振动的合成问题. (1) t + → 存在一一对应的关系; (x,v) (2)相位在 0 ~ 2 内变化,质点 π 无相同的运动状态; 二 相位 t + (3)初相位(t = 0)描述质点初始时刻的运动状态. 相差 2n(n为整数)质点运动状态全同(周期性). ( 取 [−π 或 →π] ) [0→2π]
机械振动内容提要 四 简谐运动的能量 E E=Ek+Ep=k 2 1 3T 42 4 2 五两个同方向同频率简谐运动的合成 (1) 两个同方向同频率简谐运动合成后仍为简谐运动 x=x+x2=Acos(ot+o) A=2+2+2442 cos(2-)
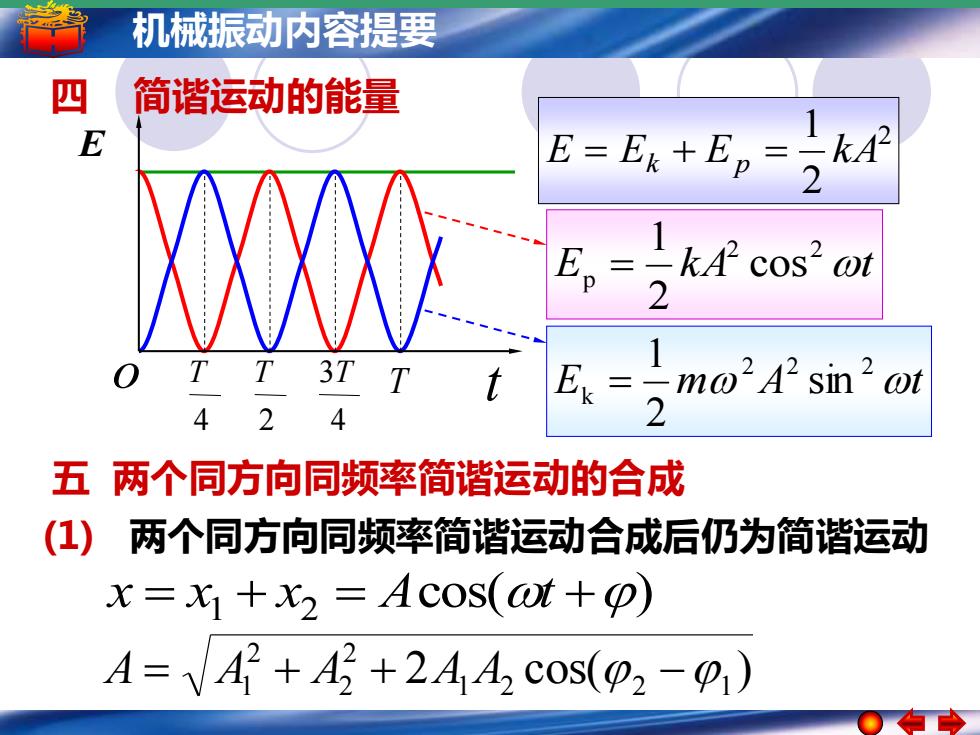
机械振动内容提要 四 简谐运动的能量 2 2 1 E = Ek + Ep = k A 4 T 2 T 4 3T E o T t E k A t 2 2 p cos 2 1 = E m A t 2 2 2 k sin 2 1 = 五 两个同方向同频率简谐运动的合成 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − cos( ) x = x1 + x2 = A t + (1) 两个同方向同频率简谐运动合成后仍为简谐运动

机械振动内容提要 A=V√4+A+2A,A2c0s△p Ap=241 2k元 A-A+A 加强 减弱 (k=0,±1,±2,) (2) 两个同方向不同频率简谐运动合成 频率较大而频率之差很小的两个同方向简谐运动的 合成,其合振动的振幅时而加强时而减弱的现象叫拍 V=V2一V一拍频(振幅变化的频率 ) (3)相互垂直的两个同频率简谐运动,合运动轨迹一般为 椭圆,其具体形状等决定于两分振动的相位差和振幅
机械振动内容提要 (2) 两个同方向不同频率简谐运动合成 频率较大而频率之差很小的两个同方向简谐运动的 合成,其合振动的振幅时而加强时而减弱的现象叫拍. = 2 − 1 拍频(振幅变化的频率) = + + 2 1 2 cos 2 2 2 A A1 A A A (k = 0,1, 2, ) 2k π A = A1 + A2 (2k +1) π A = A1 − A2 = 加强 减弱 (3) 相互垂直的两个同频率简谐运动,合运动轨迹一般为 椭圆,其具体形状等决定于两分振动的相位差和振幅