
历些毛子种枚大学 第一章:绪论 XIDIAN UNIVERSITY 内容 (1)复杂网络发展历程 (2)群体智能发展历程 (3)为什么《复杂网络与群体智能》
内容 (1)复杂网络发展历程 (2)群体智能发展历程 (3)为什么《复杂网络与群体智能》 第一章:绪论

历些毛子代枝大学 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 1:七桥问题。 复杂网络是用图来描述的,图论的发展起于18世纪欧拉对七桥问题的研究, 即“Konigsberg七桥问题”: 在18世纪东普鲁士的哥尼斯堡(Konigsberg)(今俄罗斯加里宁格勒市,) 有七座桥,连接着由普雷戈里亚(Pregolya)河分割而成的两个岛屿和两大 陆地。 一个人能否在一次散步中走过所有七座桥 ,每座桥只经过一次,最后返回原地?
复杂网络的发展历程 1:七桥问题。 复杂网络是用图来描述的,图论的发展起于18世纪欧拉对七桥问题的研究, 即 “Konigsberg 七桥问题”: 在18世纪东普鲁士的哥尼斯堡(Königsberg)(今俄罗斯加里宁格勒市,) 有七座桥,连接着由普雷戈里亚(Pregolya)河分割而成的两个岛屿和两大 陆地。 第一章:绪论 4 一个人能否在一次散步中走过所有七座桥 ,每座桥只经过一次,最后返回原地?
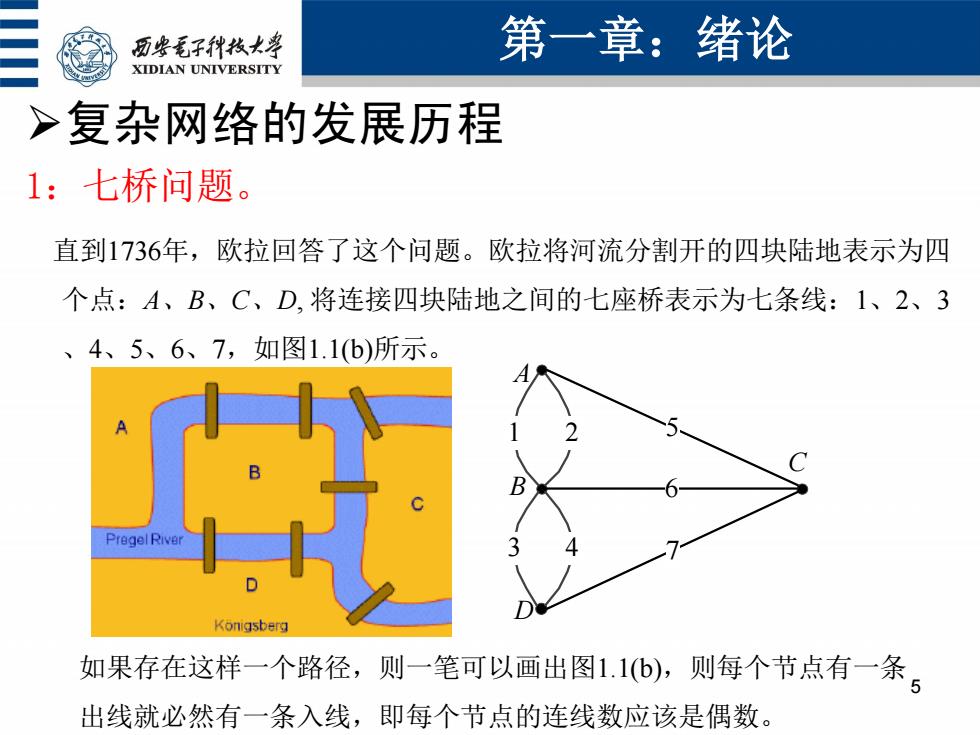
面些毛子种枝大票 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 1:七桥问题。 直到1736年,欧拉回答了这个问题。欧拉将河流分割开的四块陆地表示为四 个点:A、B、C、D,将连接四块陆地之间的七座桥表示为七条线:1、2、3 、4、5、6、7,如图1.1(b)所示。 Pregel River 如果存在这样一个路径,则一笔可以画出图1.1b),则每个节点有一条。 出线就必然有一条入线,即每个节点的连线数应该是偶数
复杂网络的发展历程 1:七桥问题。 直到1736年,欧拉回答了这个问题。欧拉将河流分割开的四块陆地表示为四 个点:A、B、C、D, 将连接四块陆地之间的七座桥表示为七条线:1、2、3 、4、5、6、7,如图1.1(b)所示。 第一章:绪论 5 1 3 2 4 5 6 7 A B D C 如果存在这样一个路径,则一笔可以画出图1.1(b),则每个节点有一条 出线就必然有一条入线,即每个节点的连线数应该是偶数

历安毛子代枚大等 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 1:七桥问题的启示: 很多现实世界的问题,可以把它抽象成有节点和边组成的图,这就导致了图 论的产生。因此,欧拉被认为是图论之父,图1.1(b)也被称为欧拉图。实际 上图是表示网络的工具,各种网络上的问题,最终可抽象成以图表示的问题 。因此,七桥问题的解决也是网络科学发展历程中的一个重要事件。 Konigsberg 6
复杂网络的发展历程 1:七桥问题的启示: 很多现实世界的问题,可以把它抽象成有节点和边组成的图,这就导致了图 论的产生。因此,欧拉被认为是图论之父,图1.1(b)也被称为欧拉图。实际 上图是表示网络的工具,各种网络上的问题,最终可抽象成以图表示的问题 。因此,七桥问题的解决也是网络科学发展历程中的一个重要事件。 第一章:绪论 6 1 3 2 4 5 6 7 A B D C

面些毛子种枝大票 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 2:随机图理论。 在20世纪50年代末和60年代,位匈牙利数学家Erdos和Renyi建立的随机图 理论(Random graph theory)被公认是在数学上开创了复杂网络拓扑结构的系 统性分析: ER随机图有两种构建方式: (1)GN,M,先确定N个点,然后向这N个点之间撒M条边; (2)G(N,p),也是先确定N个点,任意两个不同的节点之间的连边 概率是p: Erdos和Renyit研究了随机图的一些重要性质
复杂网络的发展历程 2:随机图理论。 在20 世纪 50 年代末和 60 年代,位匈牙利数学家Erdos和Renyi建立的随机图 理论(Random graph theory)被公认是在数学上开创了复杂网络拓扑结构的系 统性分析: 第一章:绪论 ER随机图有两种构建方式: (1)G(N,M),先确定N个点,然后向这N个点之间撒M条边; (2)G(N,p),也是先确定N个点,任意两个不同的节点之间的连边 概率是p; Erdos和Renyi研究了随机图的一些重要性质

历些毛子代枝大学 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 2:随机图理论。 Edδs和Rényi系统地研究了随机图所具有的性质(比如连通性)在网络规模 增大时与概率的关系。他们最重要发现是E随机图中许多重要性质都是 随着网络规模的增大突然涌现的。比如,当给定概率p,当网络规模大于 某个临界值后,生成的随机图几乎必然是连通的。 Ed6s被称为20世纪的欧拉。ER随机图理论被认为是首个严格的和完整的 关于图的理论,为图论的阈函数和分支涌现的相变研究提供了网络,是一种 重要的数学理论。ER随机图模型也被认为是第一个复杂网络结构模型,为后 来复杂网络研究生成各种网络数据开创了先河
复杂网络的发展历程 2:随机图理论。 • Edös和 Rényi系统地研究了随机图所具有的性质(比如连通性)在网络规模 增大时与概率p的关系。他们最重要发现是 ER 随机图中许多重要性质都是 随着网络规模的增大突然涌现的。比如,当给定概率 p ,当网络规模大于 某个临界值后,生成的随机图几乎必然是连通的。 • Edös被称为 20 世纪的欧拉。ER 随机图理论被认为是首个严格的和完整的 关于图的理论,为图论的阈函数和分支涌现的相变研究提供了网络,是一种 重要的数学理论。ER随机图模型也被认为是第一个复杂网络结构模型,为后 来复杂网络研究生成各种网络数据开创了先河。 第一章:绪论

历些毛子科枚大学 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 3:小世界实验。 (1)Milgram的小世界实验 一个有趣的问题是:地球上的任意两个人,通过中间人使他们之间建立联接, 平均需要几个中间人呢? 20世纪60年代: Stanley Milgram:美国哈佛大学社会心理学家; 选择两个目标,在遥远的地方随机选择一批志愿者,通过自己所认识的人, 以自己认为最少的传递方式,把信件传递给目标。 两个目标:一个是美国马萨诸塞州沙朗的一个神学院的研究生的妻子,另一 个是在波士顿的一个证券经纪人: 志愿者:分别在遥远的堪萨斯州和内布拉斯加州招募了一批志愿者
复杂网络的发展历程 3:小世界实验。 (1) Milgram 的小世界实验 一个有趣的问题是:地球上的任意两个人,通过中间人使他们之间建立联接, 平均需要几个中间人呢? 20世纪60年代; Stanley Milgram:美国哈佛大学社会心理学家; 选择两个目标,在遥远的地方随机选择一批志愿者,通过自己所认识的人, 以自己认为最少的传递方式,把信件传递给目标。 两个目标:一个是美国马萨诸塞州沙朗的一个神学院的研究生的妻子,另一 个是在波士顿的一个证券经纪人; 志愿者:分别在遥远的堪萨斯州和内布拉斯加州招募了一批志愿者 第一章:绪论

历些毛子种枚大 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 3:小世界实验。 (1)Milgram的小世界实验 结论:地球上任意两个人的平均距离是6, 也就是说,平均只要通过中间5个人,你就可以与地球上任何一个人 发生联系: 不足:总共只发出了300封信,只有部分信件到达了目标手中,相对 于巨大的社会网络,这个样本数量是很小的。尽管实验很新颖、很有 趣,但可信度并不高。 在此之后,也有各种各样的非常有趣的关于六度分离判断的实验, 但这些实验的规模还是不够大,说服力不够,直到出现了互联网上的 小世界实验
复杂网络的发展历程 3:小世界实验。 (1) Milgram 的小世界实验 第一章:绪论 结论:地球上任意两个人的平均距离是6, 也就是说,平均只要通过中间5个人,你就可以与地球上任何一个人 发生联系; 不足:总共只发出了300封信,只有部分信件到达了目标手中,相对 于巨大的社会网络,这个样本数量是很小的。尽管实验很新颖、很有 趣,但可信度并不高。 在此之后,也有各种各样的非常有趣的关于六度分离判断的实验, 但这些实验的规模还是不够大,说服力不够,直到出现了互联网上的 小世界实验

历些毛子代枝大学 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 3:小世界实验。 (2)Internet上的小世界实验 2001年: Vatts:美国哥伦比亚大学社会学系: 建立了一个网站,在世界范围内通过网络检验六度分离理论,在13个国家选 定了18名目标对象,志愿者注册后被告知目标对象信息,以自己认为最少的传 递方式发邮件,把邮件传递给目标对象。 实现持续了一年,实验结果2003年发表在Science.上。 结果:每个邮件平均转发5-7次,即可到达目标对象
复杂网络的发展历程 3:小世界实验。 (2)Internet 上的小世界实验 2001年; Watts:美国哥伦比亚大学社会学系; 建立了一个网站,在世界范围内通过网络检验六度分离理论,在13个国家选 定了18名目标对象,志愿者注册后被告知目标对象信息,以自己认为最少的传 递方式发邮件,把邮件传递给目标对象。 实现持续了一年,实验结果2003年发表在Science上。 第一章:绪论 结果:每个邮件平均转发5-7次,即可到达目标对象

历些毛子代枝大学 第一章:绪论 XIDIAN UNIVERSITY >复杂网络的发展历程 3:小世界实验。 (2)Internet上的小世界实验:向目标对象发邮件 2001年: Vatts:美国哥伦比亚大学社会学系; 建立了一个网站,在世界范围内通过网络检验六度分离理论,在3个国家选 定了18名目标对象,志愿者注册后被告知目标对象信息,分布在世界各地的6万 多名志愿者参与了实验,有384个志愿者的邮件发到了目标对象。 实现持续了一年,实验结果2003年发表在Science.上。 结果:每个邮件平均转发5-7次,即可到达目标对象
复杂网络的发展历程 3:小世界实验。 (2)Internet 上的小世界实验: 向目标对象发邮件 2001年; Watts:美国哥伦比亚大学社会学系; 建立了一个网站,在世界范围内通过网络检验六度分离理论,在13个国家选 定了18名目标对象,志愿者注册后被告知目标对象信息,分布在世界各地的6万 多名志愿者参与了实验,有384个志愿者的邮件发到了目标对象。 实现持续了一年,实验结果2003年发表在Science上。 第一章:绪论 结果:每个邮件平均转发5-7次,即可到达目标对象