
历些花子种拔大皇 蚁群算法 XIDIAN UNIVERSITY >蚁群觅食行为描述 >蚁群算法 >蚂蚁群体智能产生机理 2
蚁群觅食行为描述 蚁群算法 蚂蚁群体智能产生机理 蚁群算法 2

历些毛子种枝大学 一、蚁群觅食行为描述 XIDIAN UNIVERSITY 1. 蚁群的群体行为 >蚂蚁在觅食过程中能够通过相互协作找到食物源和巢穴间的最短路径: >大量蚂蚁在巢穴与食物源之间形成近乎直线的路径,而不是曲线或者圆 等其他形状: >蚂蚁的视觉几乎是模糊的,身形越小视力越模糊,蚂蚁寻找路径靠的是 嗅觉;对蚂蚁进行了障碍识别实验。结果发现,大蚂蚁能分辨出17厘米以 外的障碍物,而小蚂蚁只能分辨出5厘米以外的障碍物: >蚂蚁群体不仅能完成复杂的任务,而且还能适应环境的变化,如在蚁群 运动路线上突然出现障碍物时,一开始各只蚂蚁分布是均匀的,不管路径 长短,蚂蚁总是先按同等概率选择各条路径,最终找到最短路径; 3
1. 蚁群的群体行为 蚂蚁在觅食过程中能够通过相互协作找到食物源和巢穴间的最短路径; 大量蚂蚁在巢穴与食物源之间形成近乎直线的路径,而不是曲线或者圆 等其他形状; 蚂蚁的视觉几乎是模糊的,身形越小视力越模糊,蚂蚁寻找路径靠的是 嗅觉;对蚂蚁进行了障碍识别实验。结果发现,大蚂蚁能分辨出17厘米以 外的障碍物,而小蚂蚁只能分辨出5厘米以外的障碍物; 蚂蚁群体不仅能完成复杂的任务,而且还能适应环境的变化,如在蚁群 运动路线上突然出现障碍物时,一开始各只蚂蚁分布是均匀的,不管路径 长短,蚂蚁总是先按同等概率选择各条路径,最终找到最短路径; 一、蚁群觅食行为描述 3

面些毛子种枝大” 、蚁群觅食行为描述 XIDIAN UNIVERSITY 2. 信息交换 蚂蚁在运动过程中,能够在其经过的路径上留下信息素, 而且能感知信息素存在及其强度,并以此指导自己运动的 方向。 3.行为规则 向信息素浓度高的方向移动,并在其经过的路上留下信息 素。这是一种正反馈机制,也可以将整个蚁群认定为一个 增强型学习系统。 蚂蚁对走过的路有记忆
2. 信息交换 蚂蚁在运动过程中,能够在其经过的路径上留下信息素, 而且能感知信息素存在及其强度,并以此指导自己运动的 方向。 3. 行为规则 向信息素浓度高的方向移动,并在其经过的路上留下信息 素。这是一种正反馈机制,也可以将整个蚁群认定为一个 增强型学习系统。 蚂蚁对走过的路有记忆。 一、蚁群觅食行为描述 4
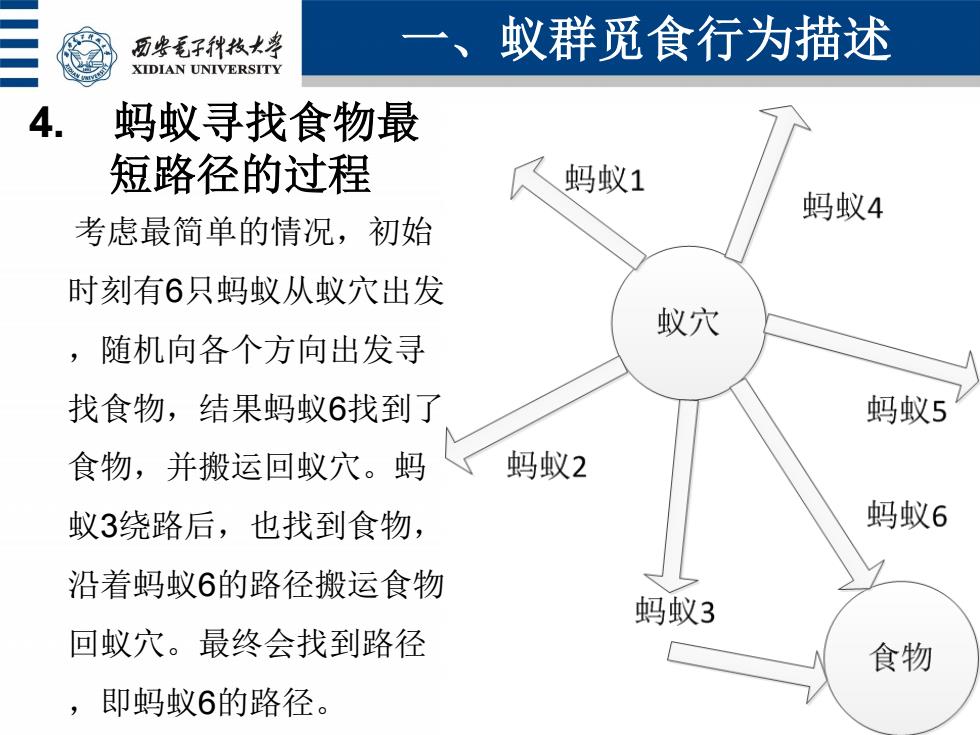
面些毛子种技大学 一、蚁群觅食行为描述 XIDIAN UNIVERSITY 4. 蚂蚁寻找食物最 短路径的过程 蚂蚁1 蚂蚁4 考虑最简单的情况,初始 时刻有6只蚂蚁从蚁穴出发 蚁穴 ,随机向各个方向出发寻 找食物,结果蚂蚁6找到了 蚂蚁5 食物,并搬运回蚁穴。蚂 蚂蚁2 蚁3绕路后,也找到食物, 蚂蚁6 沿着蚂蚁6的路径搬运食物 蚂蚁3 回蚁穴。最终会找到路径 食物 ,即蚂蚁6的路径
4. 蚂蚁寻找食物最 短路径的过程 考虑最简单的情况,初始 时刻有6只蚂蚁从蚁穴出发 ,随机向各个方向出发寻 找食物,结果蚂蚁6找到了 食物,并搬运回蚁穴。蚂 蚁3绕路后,也找到食物, 沿着蚂蚁6的路径搬运食物 回蚁穴。最终会找到路径 ,即蚂蚁6的路径。 一、蚁群觅食行为描述 5
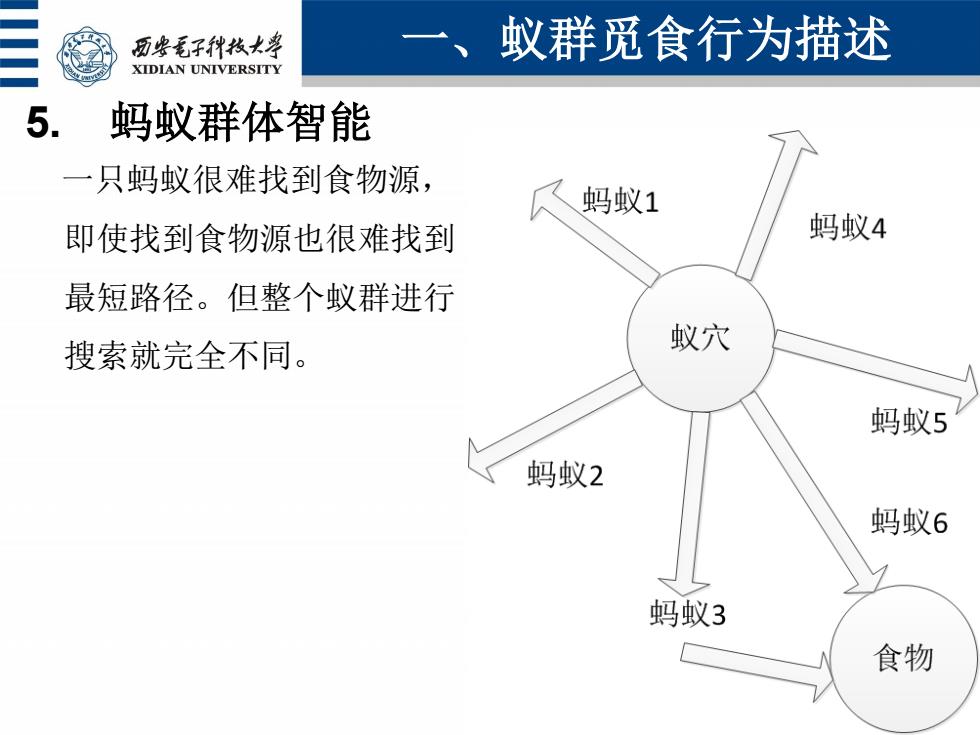
历要毛子代枚士 一、蚁群觅食行为描述 XIDIAN UNIVERSITY 5. 蚂蚁群体智能 一只蚂蚁很难找到食物源, 蚂蚁1 即使找到食物源也很难找到 蚂蚁4 最短路径。但整个蚁群进行 搜索就完全不同。 蚁穴 蚂蚁5 蚂蚁2 蚂蚁6 蚂蚁3 食物
5. 蚂蚁群体智能 一只蚂蚁很难找到食物源, 即使找到食物源也很难找到 最短路径。但整个蚁群进行 搜索就完全不同。 一、蚁群觅食行为描述 6

些毛子种技大学 二、蚁群算法 XIDIAN UNIVERSITY 蚁群算法的数学模型 >利用TSP问题来说明这个数学模型,TSP问题 可以描述为:给定一系列城市和每对城市之间 的距离,求访问每一座城市一次并回到起始城 市的最短回路。 >蚁群算法有两大步骤: ·路径构建 。 信息素更新 7
1 蚁群算法的数学模型 利用TSP问题来说明这个数学模型,TSP问题 可以描述为:给定一系列城市和每对城市之间 的距离,求访问每一座城市一次并回到起始城 市的最短回路。 蚁群算法有两大步骤: • 路径构建 • 信息素更新 二、蚁群算法 7

历要毛子代枚大” 二、 蚁群算法 XIDIAN UNIVERSITY 1 蚁群算法的数学模型 。 路径构建 每只蚂蚁都随机选择一个城市作为初始位置,按照一个随 机比例p(t)选择下一个要达到的城市。 $(t)为时刻蚂蚁k从城市转移到城市的概率,此概率由两个因 素决定,一是该路径上信息素浓度,二是城市间的距离。 50=ayru0r Σ[t(t)][m(t)]B1 jeallow k (2-1) 其中,t(t)为该该段路径上的信息素浓度 防0=击为启发函 数,即两城市距离的倒数,allow k为k可选城市集合,即未走过的 城市集合。α为信息素重要程度因子,B为启发函数因子,表示距离 的相对重要性。 8
1 蚁群算法的数学模型 • 路径构建 每只蚂蚁都随机选择一个城市作为初始位置,按照一个随 机比例 𝑝𝑖𝑗 𝑘 𝑡 选择下一个要达到的城市。 𝑝𝑖𝑗 𝑘 𝑡 为t时刻蚂蚁k从城市i转移到城市j的概率,此概率由两个因 素决定,一是该路径上信息素浓度,二是城市间的距离。 (2-1) 其中,𝜏𝑖𝑗(𝑡)为该该段路径上的信息素浓度; 𝜂𝑖𝑗 𝑡 = 1 𝑑𝑖𝑗 为启发函 数,即两城市距离的倒数, allow_k为k可选城市集合,即未走过的 城市集合。𝛼为信息素重要程度因子,𝛽为启发函数因子, 表示距离 的相对重要性。 二、蚁群算法 8 𝑝𝑖𝑗 𝑘 𝑡 = [𝜏𝑖𝑗(𝑡)] 𝛼 [𝜂𝑖𝑗(𝑡)] 𝛽 [𝜏𝑖𝑗(𝑡)] 𝛼[𝜂𝑖𝑗(𝑡)] 𝛽 , 𝑗𝜖𝑎𝑙𝑙𝑜𝑤_𝑘

历些毛子代枝大学 二、蚁群算法 XIDIAN UNIVERSITY 7 蚁群算法的数学模型 ·信息素更新 当所有蚂蚁到达终点时,必须把各路径的信息素浓度重新更新 一次,信息素的更新分为两部分:蒸发和增强 (t+1)=(1-p)*Tj(t)+∑C1△盼(2-2) 如果蚂蚁k经过路径访 △={C 0, 其他 0<p<1为信息素蒸发率,△τ为第k只蚂蚁在城市i与城市j连接路 径上释放信息素而增加的信息素浓度:Q为信息素强度,在一定程度 上影响算法的收敛速度;C为在本轮中蚂蚁所走路径的总长度
1 蚁群算法的数学模型 • 信息素更新 当所有蚂蚁到达终点时,必须把各路径的信息素浓度重新更新 一次,信息素的更新分为两部分:蒸发和增强 𝜏𝑖𝑗 𝑡 + 1 = 1 − 𝜌 ∗ 𝜏𝑖𝑗 𝑡 + ∆𝜏𝑖𝑗 𝑚 𝑘 𝑘=1 (2-2) 0 < 𝜌 < 1为信息素蒸发率,∆𝜏𝑖𝑗 𝑘 为第k只蚂蚁在城市i与城市j连接路 径上释放信息素而增加的信息素浓度;Q为信息素强度,在一定程度 上影响算法的收敛速度;Ck为在本轮中蚂蚁k所走路径的总长度。 二、蚁群算法 9 ij 0 k k Q k ij C ,如果蚂蚁 经过路径 , 其他

历安毛子代枚大” 二、蚁群算法 XIDIAN UNIVERSITY 1 蚁群算法的数学模型 >信息素更新的作用 ●信息素挥发:避免算法过快地向局部最优区域集中,有助于 搜索区域的扩展。 ●信息素增强:实现由单个蚂蚁无法实现的集中行动。基本蚁 群算法的离线更新方式是在蚁群中的m只蚂蚁全部完成n个城 市的访问后,统一对残留信息进行更新处理。 10
1 蚁群算法的数学模型 信息素更新的作用 信息素挥发:避免算法过快地向局部最优区域集中,有助于 搜索区域的扩展。 信息素增强:实现由单个蚂蚁无法实现的集中行动。基本蚁 群算法的离线更新方式是在蚁群中的m只蚂蚁全部完成n个城 市的访问后,统一对残留信息进行更新处理。 二、蚁群算法 10

面些毛子种技大皇 二、蚁群算法 XIDIAN UNIVERSITY 蚁群算法的数学模型 >总结 ·在TSP问题中,首先随机设置只蚂蚁的位置,即出发城市,且初始状态各城 市间路径上的信息素浓度相同,对每只蚂蚁构造路径,从出发城市,根据概 率公式,运用轮盘赌选择法依次选择下一个要到达的城市,直至经过所有城 市得到本轮的路径。至此m只蚂蚁便得到m条路径,即m个解向量。 ·在一轮结束之后,需要更新信息素浓度。根据公式,计算所有城市间的信息 素浓度并更新。 ·接着进行下一轮迭代,此时由更新后的信息素浓度来构造路径,如此进行迭 代,直到达到最大迭代次数或算法收敛,算法结束。 11
1 蚁群算法的数学模型 总结 • 在TSP问题中,首先随机设置m只蚂蚁的位置,即出发城市,且初始状态各城 市间路径上的信息素浓度相同,对每只蚂蚁构造路径,从出发城市,根据概 率公式,运用轮盘赌选择法依次选择下一个要到达的城市,直至经过所有城 市得到本轮的路径。至此m只蚂蚁便得到m条路径,即m个解向量。 • 在一轮结束之后,需要更新信息素浓度。根据公式,计算所有城市间的信息 素浓度并更新。 • 接着进行下一轮迭代,此时由更新后的信息素浓度来构造路径,如此进行迭 代,直到达到最大迭代次数或算法收敛,算法结束。 二、蚁群算法 11