
Xidian University 汇报内容 ■一、网络动力学模型简介 ■二、网络动力学模型与重叠社区结构 ■三、改进的动力学模型与重叠社区结构 ■四、离散动力学模型解决社区检测问题 西安电子科技大学
西安电子科技大学 汇报内容 一、网络动力学模型简介 二、网络动力学模型与重叠社区结构 三、改进的动力学模型与重叠社区结构 四、离散动力学模型解决社区检测问题
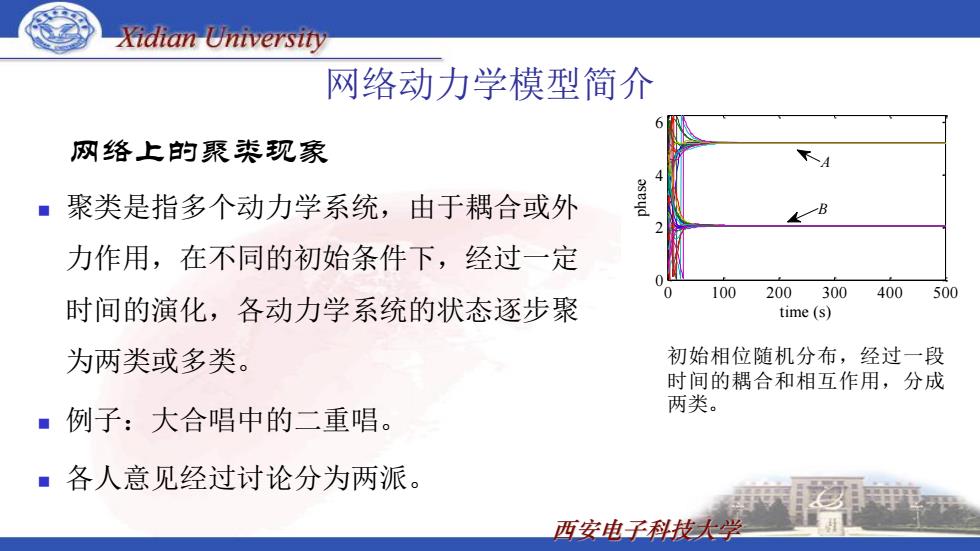
Xidian University 网络动力学模型简介 网络上的聚类现象 聚类是指多个动力学系统,由于耦合或外 B 力作用,在不同的初始条件下,经过一定 100 200300 400 500 时间的演化,各动力学系统的状态逐步聚 time(s) 为两类或多类。 初始相位随机分布,经过一段 时间的耦合和相互作用,分成 ■例子:大合唱中的二重唱。 两类。 ■各人意见经过讨论分为两派。 西安电子科技大学
西安电子科技大学 网络上的聚类现象 聚类是指多个动力学系统,由于耦合或外 力作用,在不同的初始条件下,经过一定 时间的演化,各动力学系统的状态逐步聚 为两类或多类。 例子:大合唱中的二重唱。 各人意见经过讨论分为两派。 初始相位随机分布,经过一段 时间的耦合和相互作用,分成 两类。 网络动力学模型简介 0 100 200 300 400 500 0 2 4 6 time (s) phase A B

Xidian University 网络动力学模型简介 ■网络功力学模型 经典的Kuramoto模型 e=+路a斯sin(0,-)i=1,N.( 其中,日、⊙、k分别表示节点的相位、频率和度, 0110 c表示节点间的耦合强度。 1011 [a]表示网络邻接矩阵:节点i与节点j之间存在连边, [a= 1101 ayl:否则,ay0。 0110 网络及其邻接矩阵 这个模型可以研究网络的聚类现象吗? 西安电子科技大学
西安电子科技大学 A D C B 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 [aij] 网络及其邻接矩阵 网络动力学模型简介 网络动力学模型 经典的Kuramoto模型 这个模型可以研究网络的聚类现象吗?

Xidian University 目录 ■一、网络动力学模型简介 ■二、重叠社区网络上的动力学现象 ■三、改进的动力学模型与重叠社区结构 ■四、离散动力学模型解决社区检测问题 西安电子科技大学
西安电子科技大学 目录 一、网络动力学模型简介 二、重叠社区网络上的动力学现象 三、改进的动力学模型与重叠社区结构 四、离散动力学模型解决社区检测问题

Xidian University 重叠社区网络上的动力学现象 ■随机生成社区网络: 具有重叠社区结构的随机网络G,共N个节点,分为 两个社区A、B,两社区重叠部分为O,重叠度s定义为: S= IlAOBII (4) IAUBII 随机连接网络中的节点对,社区A、B内的节点对连 接概率为P1,社区A、B之间的节点对连接概率为P11, 比P1小得多,重叠部分O中节点对连接概率为P0,O中 节点与社区A、B中节点的连接概率分别为P01oA 随机网络示例 P01oB,合称P01。 西安电子科技大学
西安电子科技大学 随机网络示例 重叠社区网络上的动力学现象 随机生成社区网络:

Xidian University 重叠社区网络上的动力学现象 随机生成社区网络: AB AB 随机网络示例.节点数N=400,社区A、B和重叠区域O内节点对的连接概率 P1=P0=0.1,社区A、B之间的节点对连接概率P11=0.001,(a)s=0.1,p01=0.1: b)s=0.1,p01=0.05;(c)s=0.2,p010A=0.03,p010B=0.06 西安电子科技大学
西安电子科技大学 b 随机网络示例. 节点数N=400,社区A、B和重叠区域O内节点对的连接概率 P1=P0=0.1,社区A、B之间的节点对连接概率P11=0.001, (a) s = 0.1, p01 = 0.1; (b) s = 0.1, p01 = 0.05; (c) s = 0.2, p01OA = 0.03, p01OB = 0.06 随机生成社区网络: 重叠社区网络上的动力学现象 a c

Xidian University 重叠社区网络上的动力学现象 斯量网络同步的参数 参数M用以衡量Kuramoto模型中网络的同步程度: "-2 (5) 其中,N是节点数目。如果模型中的耦合参数c为0,即节 点间耦合强度为0,那么内是1/的序列;如果节点达到 完全同步,那么M会无限接近1。 西安电子科技大学
西安电子科技大学 重叠社区网络上的动力学现象 衡量网络同步的参数 参数M用以衡量Kuramoto模型中网络的同步程度: (5) 其中,N是节点数目。如果模型中的耦合参数c为0,即节 点间耦合强度为0,那么 内是 的序列;如果节点达到 完全同步,那么M会无限接近1
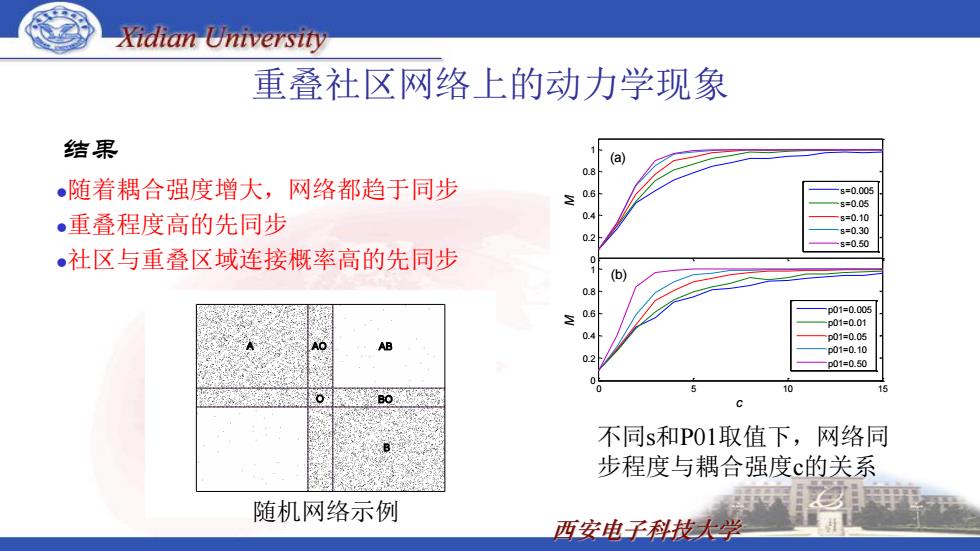
Xidian University 重叠社区网络上的动力学现象 结果 (a) 。随着耦合强度增大,网络都趋于同步 s=0.00 s=0.05 。重叠程度高的先同步 s=0.10 8=0.30 0.2 5=0.50 •社区与重叠区域连接概率高的先同步 (b) 0.8 p01=0.005 p01=0.01 04 p01=0.05 AB p01=0.10 p01=0.50 不同s和P01取值下,网络同 步程度与耦合强度c的关系 随机网络示例 西安电子科技大学
西安电子科技大学 结果 随着耦合强度增大,网络都趋于同步 重叠程度高的先同步 社区与重叠区域连接概率高的先同步 重叠社区网络上的动力学现象 0 0.2 0.4 0.6 0.8 1 M s=0.005 s=0.05 s=0.10 s=0.30 s=0.50 0 5 10 15 0 0.2 0.4 0.6 0.8 1 c M p01=0.005 p01=0.01 p01=0.05 p01=0.10 p01=0.50 (a) (b) 不同s和P01取值下,网络同 步程度与耦合强度c的关系 随机网络示例
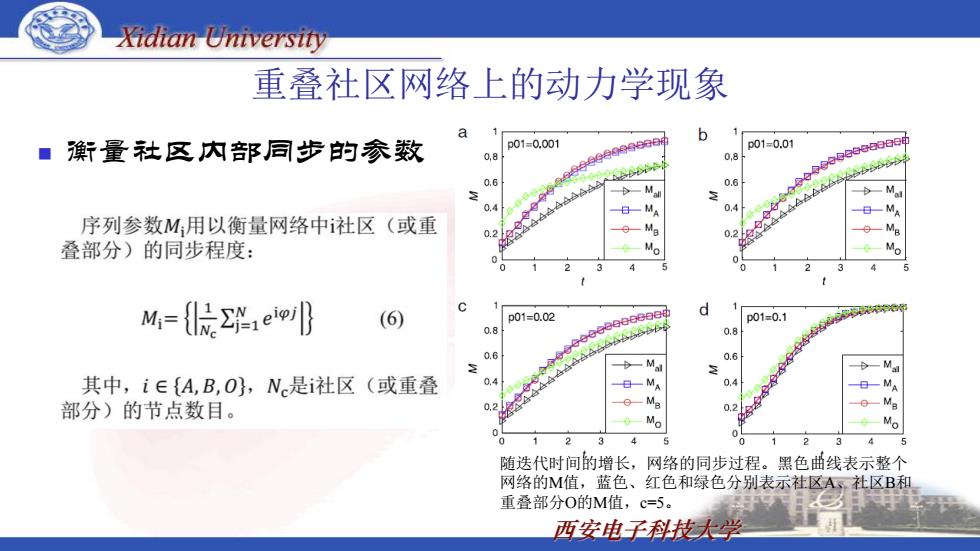
Xidian University 重叠社区网络上的动力学现象 a b ■鼾量社区内部同步的参数 p01=0.001 p01=0.01 0,8 0,8 06 0.6 D一M 0.4 04 一M 序列参数M,用以衡量网络中社区(或重 0. 0.2 Me 叠部分)的同步程度: M 2 M,={促兴,e} (6) p01=0.02 d p01=0.1 08 0.8 0.6 0.6 一M 一M 其中,i∈{A,B,O,N是社区(或重叠 0.4 0.4 部分)的节点数目。 0.2 0.2 M。 Mo 34 随迭代时间的增长,网络的同步过程。黑色曲线表示整个 网络的M值,蓝色、红色和绿色分别表示社区A社区B和 重叠部分O的M值,c=5。 西安电子科技大学
西安电子科技大学 重叠社区网络上的动力学现象 随迭代时间的增长,网络的同步过程。黑色曲线表示整个 网络的M值,蓝色、红色和绿色分别表示社区A、社区B和 重叠部分O的M值,c=5。 衡量社区内部同步的参数
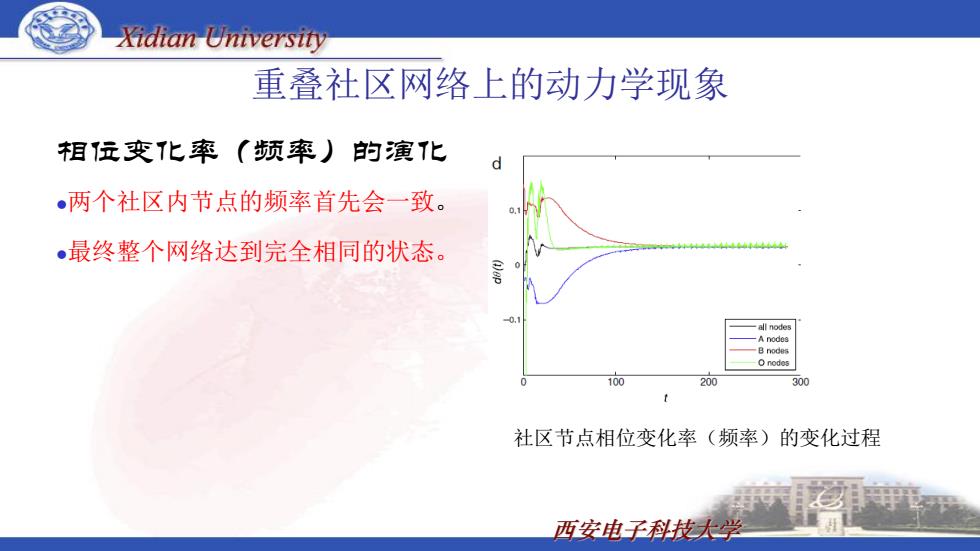
Xidian University 重叠社区网络上的动力学现象 相阮变化率(频率)的演T化 d 。两个社区内节点的频率首先会一致。 ●最终整个网络达到完全相同的状态。 4444444044 all nodes A nodes -B nodes 100 200 300 社区节点相位变化率(频率)的变化过程 西安电子科技大学
西安电子科技大学 重叠社区网络上的动力学现象 相位变化率(频率)的演化 两个社区内节点的频率首先会一致。 最终整个网络达到完全相同的状态。 社区节点相位变化率(频率)的变化过程