西安电子科技大学：《复杂网络与群体智能》课程教学课件（研究生）第七讲 最小生成树社区检测

历华毛子代枝大” 第八讲：最小生成树-社区检测 XIDIAN UNIVERSITY >最小生成树 >基于最小生成树的社区检测 2

最小生成树 基于最小生成树的社区检测 第八讲：最小生成树-社区检测 2

历些毛子种枝大票 最小生成树 XIDIAN UNIVERSITY 1. 什么是最小生成树(minimum spanning tree)? 所谓最小生成树，就是在一个具有N个顶点的加权连通图G 中，如果存在某个树形子图T,其包含了图G中的所有项点和 一部分边，且不形成回路，并且子图T的各边权值（距离）之 和最小，则称T为图G的最小生成树。 0.55 0.5」 0.5 12 15 12 15 0.43 0.5\0.55 0.5 0.43 0.75 0.75 0.43 0.55 0.5 0.43 /0.46 0.46 0.46 0.43 13 10 0.55 0.43 八14/0.43 0.460.75 0.46 0.75 0.6 > 0.43 15 0.55 0.75 0.60.75 0.75 0.75 0.55 .75 0.75 图1.一个网络与它的最小生成树 3

1. 什么是最小生成树（minimum spanning tree ）？ 所谓最小生成树，就是在一个具有N个顶点的加权连通图G 中，如果存在某个树形子图T，其包含了图G中的所有顶点和 一部分边，且不形成回路，并且子图T的各边权值（距离）之 和最小，则称T为图G的最小生成树。 最小生成树 3 0.55 0.55 0.75 0.75 0.6 0.46 0.46 0.43 0.46 0.6 0.5 0.5 0.43 0.75 0.75 0.75 0.75 0.43 0.5 0.55 0.5 0.43 0.55 0.55 0.55 0.43 10 9 11 14 12 15 7 3 5 2 1 6 4 a 8 0.75 13 0.43 0.75 0.6 0.46 0.46 0.43 0.75 0.75 0.5 0.43 0.5 0.43 0.55 0.75 10 9 11 13 14 12 15 5 1 6 2 7 4 3 8 b 图1. 一个网络与它的最小生成树

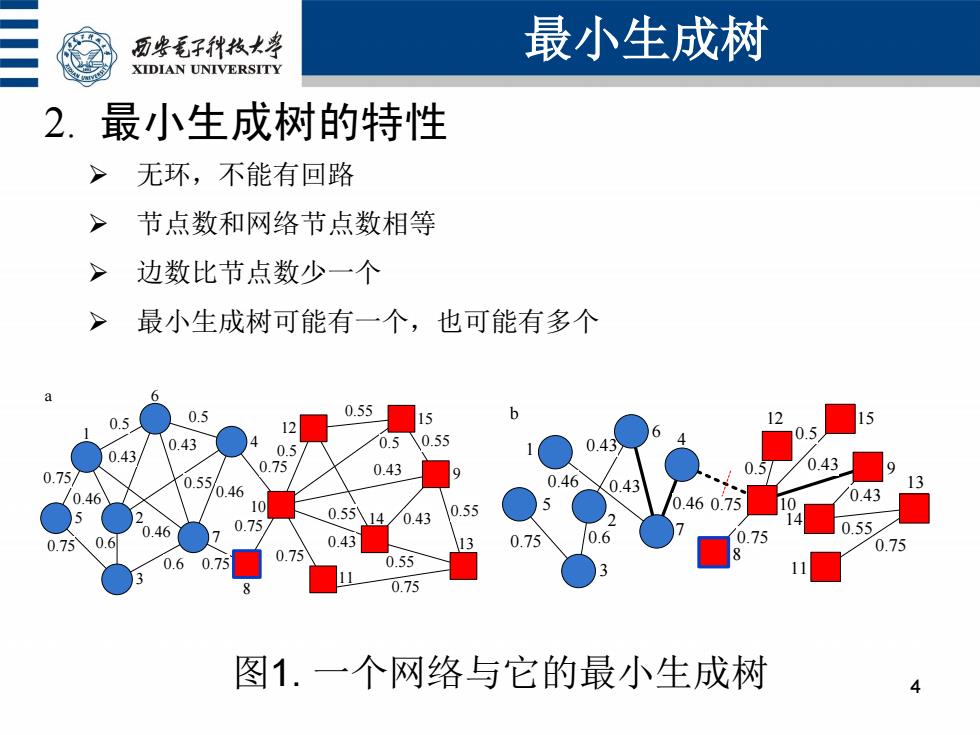
历安毛子代枚大等 最小生成树 XIDIAN UNIVERSITY 2.最小生成树的特性 > 无环，不能有回路 节点数和网络节点数相等 > 边数比节点数少一个 > 最小生成树可能有一个，也可能有多个 0.55 0.5 0.5 15 12 0.43 4 0.5 0.5 0.55 4 0.43 0.75 0.75/ 0.43 0.43 0.55 0.46 0.43 13 /0.46 0.46 10 0.55 0.460.75 0.43 5 0.46 > 0.75 0.55八14 0.43 0.55 0.75 0.6 0.43 0.75 0.6 0.75 0.75 0.6 0.75 0.75 0.55 f 0.75 图1.一个网络与它的最小生成树 4

2. 最小生成树的特性  无环，不能有回路  节点数和网络节点数相等  边数比节点数少一个  最小生成树可能有一个，也可能有多个 最小生成树 4 0.55 0.55 0.75 0.75 0.6 0.46 0.46 0.43 0.46 0.6 0.5 0.5 0.43 0.75 0.75 0.75 0.75 0.43 0.5 0.55 0.5 0.43 0.55 0.55 0.55 0.43 10 9 11 14 12 15 7 3 5 2 1 6 4 a 8 0.75 13 0.43 0.75 0.6 0.46 0.46 0.43 0.75 0.75 0.5 0.43 0.5 0.43 0.55 0.75 10 9 11 13 14 12 15 5 1 6 2 7 4 3 8 b 图1. 一个网络与它的最小生成树

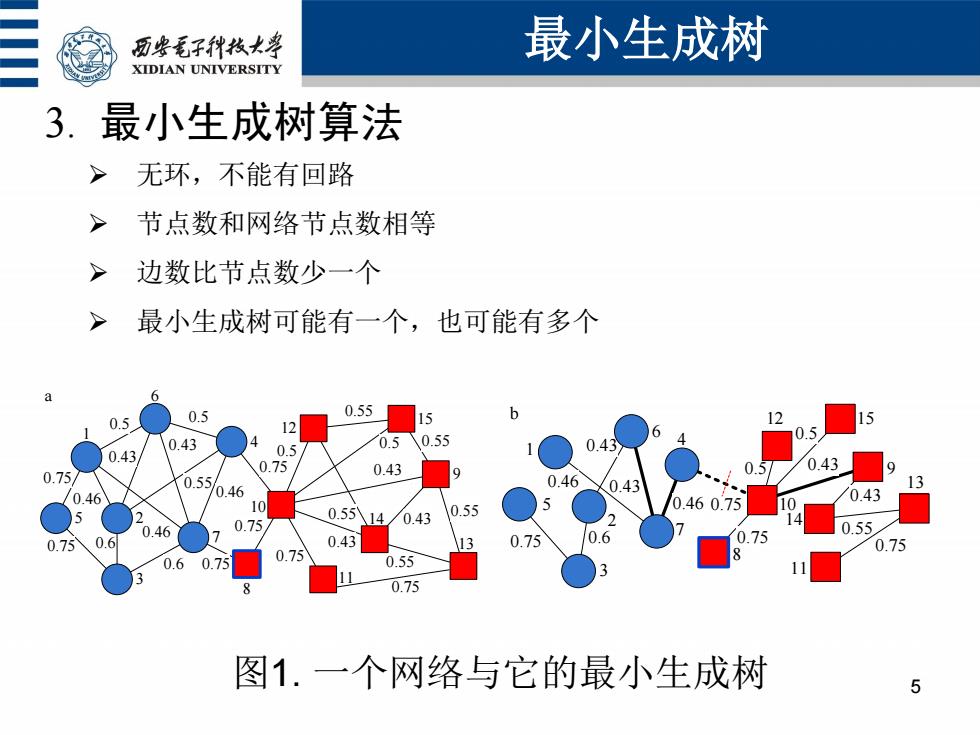
历安毛子代枚大” 最小生成树 XIDIAN UNIVERSITY 3. 最小生成树算法 > 无环，不能有回路 节点数和网络节点数相等 > 边数比节点数少一个 最小生成树可能有一个，也可能有多个 0.55 0.5 0.5 12 12 15 0.43 4 0.5 0.55 0.43 0.43 .5 0.75 0.43 0.43 0.75 0.55 0.46 0.46 0.46 0.43 0.43 10 5 0.55八14 /0.43 0.55 .460.75 0.46 0.75 0.55 0.75 0.6 7 0.43 0. 0.75 0.6 0.75 0.75 0.55 0.75 图1.一个网络与它的最小生成树 5

3. 最小生成树算法  无环，不能有回路  节点数和网络节点数相等  边数比节点数少一个  最小生成树可能有一个，也可能有多个 最小生成树 5 0.55 0.55 0.75 0.75 0.6 0.46 0.46 0.43 0.46 0.6 0.5 0.5 0.43 0.75 0.75 0.75 0.75 0.43 0.5 0.55 0.5 0.43 0.55 0.55 0.55 0.43 10 9 11 14 12 15 7 3 5 2 1 6 4 a 8 0.75 13 0.43 0.75 0.6 0.46 0.46 0.43 0.75 0.75 0.5 0.43 0.5 0.43 0.55 0.75 10 9 11 13 14 12 15 5 1 6 2 7 4 3 8 b 图1. 一个网络与它的最小生成树

历安毛子代枚大学 最小生成树 XIDIAN UNIVERSITY 3.克鲁斯卡尔算法(Kruskal Algorithm) 第一步：在带权连通图中，将边的权值排序； 第二步：从权值最小的边开始，判断是否需要选择这条边。判断 的依据是边的两个顶点是否已连通，如果连通则继续下一条；如 果不连通，那么就选择使其连通。 连通时，要做如下判断：这两个点是否在己找到点的集合中 出现过？①.如果两个点都没有出现过，那么将这两个点都加入已 找到点的集合中；②如果其中一个点在集合中出现过，那么将另 一个没有出现过的点加入到集合中；③如果这两个点都出现过， 则不用加入到集合中。 第三步：循环第二步，直到图中所有的顶点都在子图中，即得到 最小生成树。 6

3. 克鲁斯卡尔算法(Kruskal Algorithm) 第一步：在带权连通图中，将边的权值排序； 第二步：从权值最小的边开始，判断是否需要选择这条边。判断 的依据是边的两个顶点是否已连通，如果连通则继续下一条；如 果不连通，那么就选择使其连通。 连通时，要做如下判断： 这两个点是否在已找到点的集合中 出现过？ ①.如果两个点都没有出现过，那么将这两个点都加入已 找到点的集合中；②.如果其中一个点在集合中出现过，那么将另 一个没有出现过的点加入到集合中；③.如果这两个点都出现过， 则不用加入到集合中。 第三步：循环第二步，直到图中所有的顶点都在子图中，即得到 最小生成树。 最小生成树 6

历柴毛子代枚大学 最小生成树 XIDIAN UNIVERSITY 4.Prim算法（加点法) G=(V,E)为一图，其中V为顶点的集合，E为边的集合 第一步：从某一顶点1出发，选择与它相连的具有最小权值的边(1， ),将其顶点加入到生成树顶点集合U中。U用于存放G的最小 生成树中的顶点，F存放G的最小生成树中的边。初始时刻： U={v1};F={}。 第二步：重复上述步骤 以后每一步从U中选择一个顶点而另一个顶点属于V-U的边中 ,选取具有最小权值的边(，y),将顶点加入集合U中，将 边(i,)加入集合F中； 如此不断重复，直到U=V时，最小生成树构造完毕，这时集合F中 包含了最小生成树的所有边

4. Prim算法（加点法） G=(V,E)为一图，其中V为顶点的集合，E为边的集合 第一步：从某一顶点v1出发，选择与它相连的具有最小权值的边(v1, vi)，将其顶点vi加入到生成树顶点集合U中。U用于存放G的最小 生成树中的顶点，F存放G的最小生成树中的边。初始时刻： U={v1} ；F={ }。 第二步：重复上述步骤 以后每一步从U中选择一个顶点vi, 而另一个顶点vj属于V-U的边中 ，选取具有最小权值的边（vi ， vj ），将顶点vj加入集合U中，将 边（ vi ，vj ）加入集合F中; 如此不断重复，直到U=V时，最小生成树构造完毕，这时集合F中 包含了最小生成树的所有边。 最小生成树 7

历安毛子代枚大等 基于最小生成树的社区检测 XIDIAN UNIVERSITY 1.社区网络最小生成树的特征 >在最小生产树上，社区之间的边距离较长；社区内的边 距离较短。利用这个特征就可以基于最小生成树进行社 区检测。 人 叶子节点和其它节点的连接距离较长。 0.55 0.5 0.5 15 12 0.43 0.5 0.55 0.43 0.s 0.7 0.43 0.43 0.75/ 0.55 0.46 0.46 0.43 0.46 0.460.75 0.43 10 0.55 0.75 0.55八14 0.43 0.55 0.75 0.6 0.46 1 0.43 0.75 0.6 0.75 0.6 0.75 0.75 0.55 0.75 图1.一个网络与它的最小生成树 8

1. 社区网络最小生成树的特征  在最小生产树上，社区之间的边距离较长；社区内的边 距离较短。利用这个特征就可以基于最小生成树进行社 区检测。  叶子节点和其它节点的连接距离较长。 基于最小生成树的社区检测 8 0.55 0.55 0.75 0.75 0.6 0.46 0.46 0.43 0.46 0.6 0.5 0.5 0.43 0.75 0.75 0.75 0.75 0.43 0.5 0.55 0.5 0.43 0.55 0.55 0.55 0.43 10 9 11 14 12 15 7 3 5 2 1 6 4 a 8 0.75 13 0.43 0.75 0.6 0.46 0.46 0.43 0.75 0.75 0.5 0.43 0.5 0.43 0.55 0.75 10 9 11 13 14 12 15 5 1 6 2 7 4 3 8 b 图1. 一个网络与它的最小生成树

历安毛子种枝大学 基于最小生成树的社区检测 XIDIAN UNIVERSITY 2.产生距离矩阵 >距离矩阵和相似性矩阵的区别； >距离矩阵的产生： 以公式(1)计算节点v和节点y之间的距离 1 d na1/1+nb1/2+nc1/3 (1) 其中，na,nb,nc分别为一阶路径、二阶路径、三阶路径的个数； >去掉叶子节点产生距离矩阵； >用Kruskal Algorithm算法或者Prim算法得到最小生成树 9

2. 产生距离矩阵  距离矩阵和相似性矩阵的区别；  距离矩阵的产生： 以公式（1）计算节点vi和节点vj之间的距离 （1） 其中， na,nb, nc分别为一阶路径、二阶路径、三阶路径的个数； 去掉叶子节点产生距离矩阵； 用Kruskal Algorithm算法或者Prim算法得到最小生成树 基于最小生成树的社区检测 9

历些毛子种技大皇 基于最小生成树的社区检测 XIDIAN UNIVERSITY 3.第2轮最小生成树（2nd-MST) >什么是第2轮最小生成树。 也是最小生成树，但不能有和第1轮最小生成树重复的边。 >第2轮最小生成树的产生： 网络中删除1st-MST中存在的边，重新产生最小生成树； 等价于在距离矩阵中将1st-MST存在点边赋值无穷大。 >2nd-MST和1st-MST具有相同的特性。 10

3. 第2轮最小生成树（ 2nd-MST）  什么是第2轮最小生成树。 也是最小生成树，但不能有和第1轮最小生成树重复的边。  第2轮最小生成树的产生： 网络中删除1st-MST中存在的边，重新产生最小生成树； 等价于在距离矩阵中将1st-MST存在点边赋值无穷大。 2nd-MST和 1st-MST具有相同的特性。 基于最小生成树的社区检测 10

历安毛子种枝大学 基于最小生成树的社区检测 XIDIAN UNIVERSITY 3.第2轮最小生成树（2nd-MST) a 0.5 0.55 0.5 15 12 0.43 4 0.5 0.55 0.43 0.75 0.75/ 0.43 0.55 0.46 0.46 10 0.5514/0.43 0.55 0.46 0.75 0.75 0.6 0.43 0.6 0.75 0.75 0.55 0.75 b 12 15 0.5 0.5 0.55 0.55 0.5 0.43 0.75 0.55 0.46 0.43 0 0.43 0.43 0.55 0.460.75 0.55 0.75 0.75 0.75

3. 第2轮最小生成树（ 2nd-MST）  什么是第2轮最小生成树。 也是最小生成树，但不能有和第1轮最小生成树重复的边。  第2轮最小生成树的产生： 网络中删除1st-MST中存在的边，重新产生最小生成树； 等价于在距离矩阵中将1st-MST存在点边赋值无穷大。 2nd-MST和 1st-MST具有相同的特性。 基于最小生成树的社区检测 11