
模 拟 电子 技术 第六章 集成电路运算放大器的线性应用 6.1一般问题 6.2基本运算电路 6.3对数和指数运算电路 6.4 集成模拟乘法器 6.5 有源滤波电路 小结
模 拟 电 子 技 术 集成电路运算放大器的线性应用 第 六章 小结 6.1 一般问题 6.2 基本运算电路 6.3 对数和指数运算电路 6.4 集成模拟乘法器 6.5 有源滤波电路
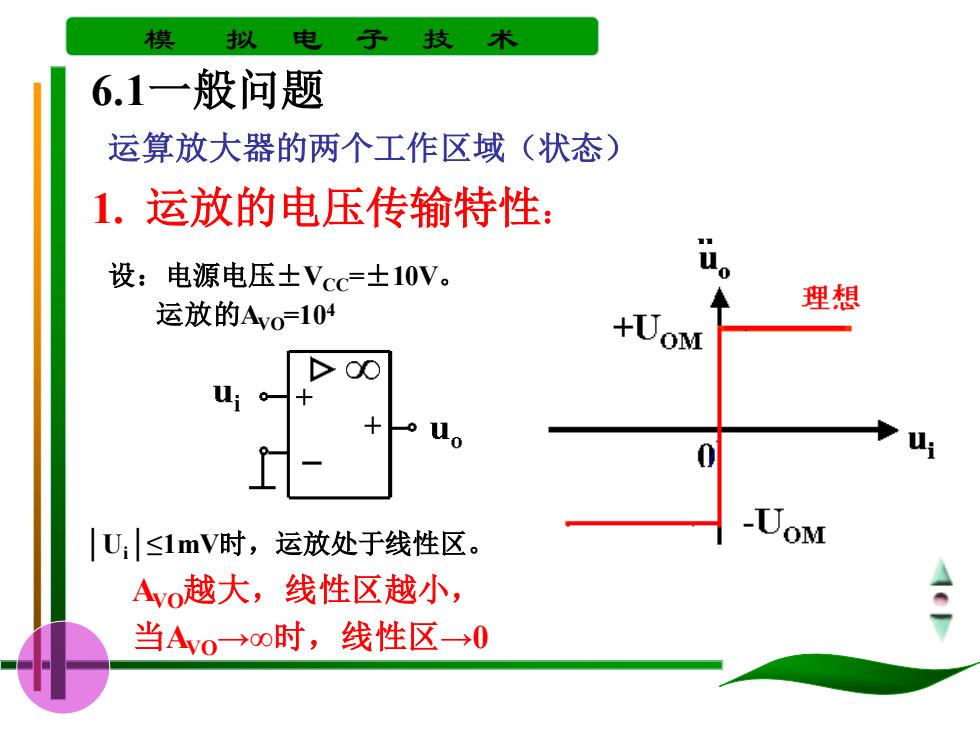
模 拟 电 子 技 6.1一般问题 运算放大器的两个工作区域(状态) 1.运放的电压传输特性: 设:电源电压士Vcc=士10V。 运放的Avo=104 理想 +UoM *0 o 0 U≤1mV时,运放处于线性区。 UoM Ao越大,线性区越小, 当Avo→o时,线性区→0
模 拟 电 子 技 术 运算放大器的两个工作区域(状态) 1. 运放的电压传输特性: 设:电源电压±VCC=±10V。 运放的AVO=104 │Ui│≤1mV时,运放处于线性区。 AVO越大,线性区越小, 当AVO→∞时,线性区→0 6.1一般问题
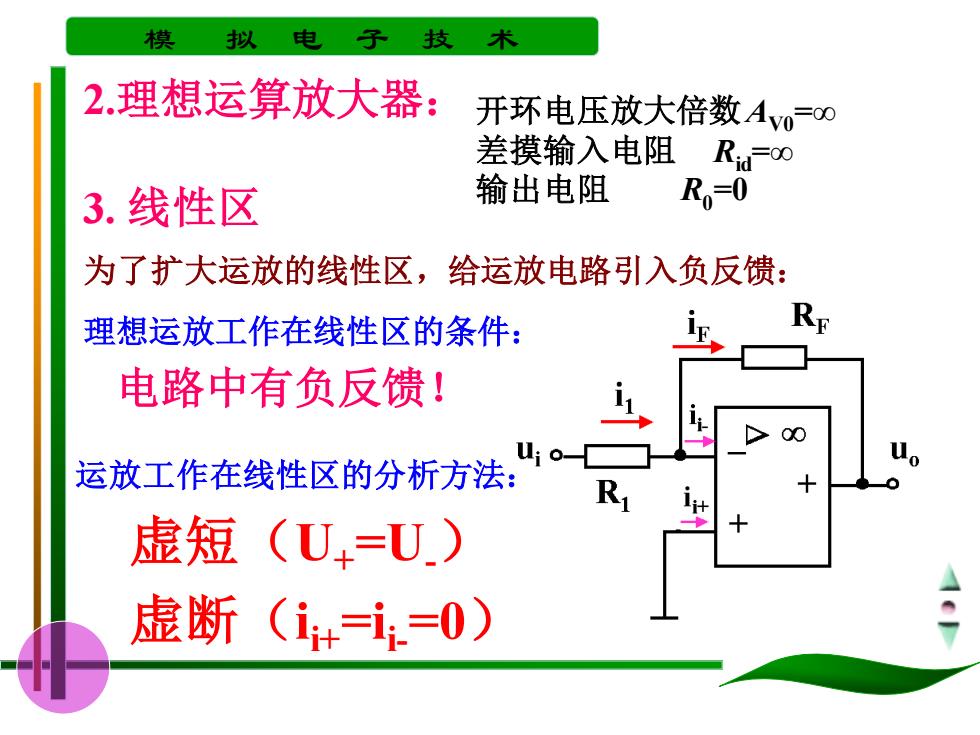
模 拟 电 子 技术 2.理想运算放大器: 开环电压放大倍数A0=0 差摸输入电阻 Ra00 3.线性区 输出电阻 R=0 为了扩大运放的线性区,给运放电路引入负反馈: 理想运放工作在线性区的条件: iF. RE 电路中有负反馈! 运放工作在线性区的分析方法: R 虚短(U=U) 虚断(1+=i=0)
模 拟 电 子 技 术 2.理想运算放大器: 开环电压放大倍数AV0=∞ 差摸输入电阻 Rid=∞ 输出电阻 R0 =0 为了扩大运放的线性区,给运放电路引入负反馈: 理想运放工作在线性区的条件: 电路中有负反馈! 运放工作在线性区的分析方法: 虚短(U+=U-) 虚断(i i+=ii-=0) 3. 线性区
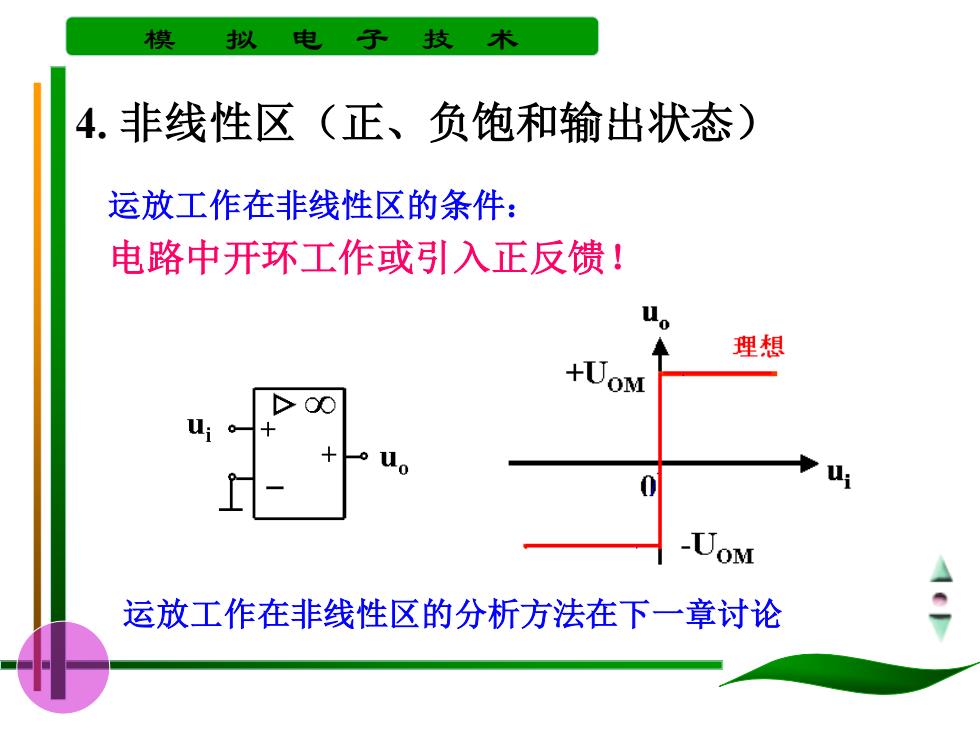
模 拟 电 子 技 4.非线性区(正、负饱和输出状态) 运放工作在非线性区的条件: 电路中开环工作或引入正反馈! 理想 +UoM 00 0 UoM 运放工作在非线性区的分析方法在下一章讨论
模 拟 电 子 技 术 4. 非线性区(正、负饱和输出状态) 运放工作在非线性区的条件: 电路中开环工作或引入正反馈! 运放工作在非线性区的分析方法在下一章讨论
模 拟 电子 技术 6.2 基本运算电路 6.2.1比例运算 6.2.2加法与减法运算 6.2.3微分与积分运算 6.2.4基本运算电路应用举例 A
模 拟 电 子 技 术 6.2 基本运算电路 6.2.1 比例运算 6.2.2 加法与减法运算 6.2.3 微分与积分运算 6.2.4 基本运算电路应用举例
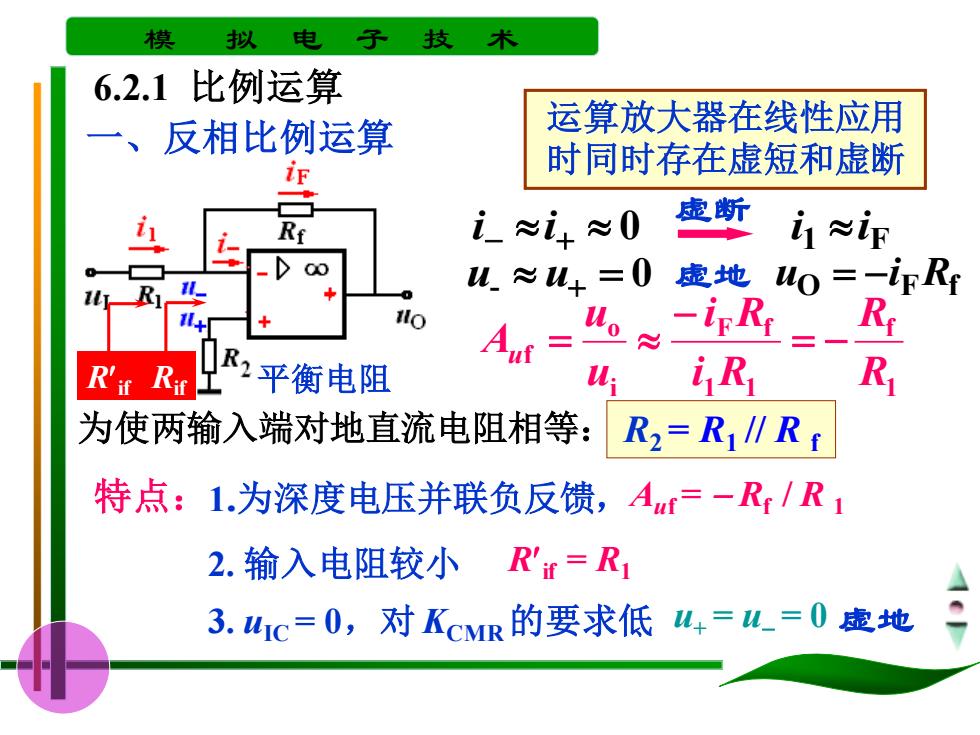
模 拟 电 子 技 6.2.1比例运算 一、反相比例运算 运算放大器在线性应用 ig 时同时存在虚短和虚断 i≈i0 虚断 p W.≈W+=0 虚地 uo =-ir Ry + Aut ≈ Rt= Ri RrRR:平衡电阻 4 iR R 为使两输入端对地直流电阻相等: R2=R1∥Rt 特点:1.为深度电压并联负反馈,Aut=-R/R1 2.输入电阻较小R'r=R1 3.u1c=0,对KcR的要求低 山4=山_=0虚地
模 拟 电 子 技 术 6.2.1 比例运算 一、反相比例运算 运算放大器在线性应用 时同时存在虚短和虚断 i − i + 0 虚断 1 F i i u- u+ = 0 虚地 O F Rf u = −i 1 f 1 1 F f i o f R R i R i R u u Au = − − = 为使两输入端对地直流电阻相等: R2 = R1 // R f 平衡电阻 特点:1.为深度电压并联负反馈,Auf = − Rf / R 1 2. 输入电阻较小 R Rif if R if = R1 3. uIC = 0,对 KCMR 的要求低 u+ = u− = 0 虚地
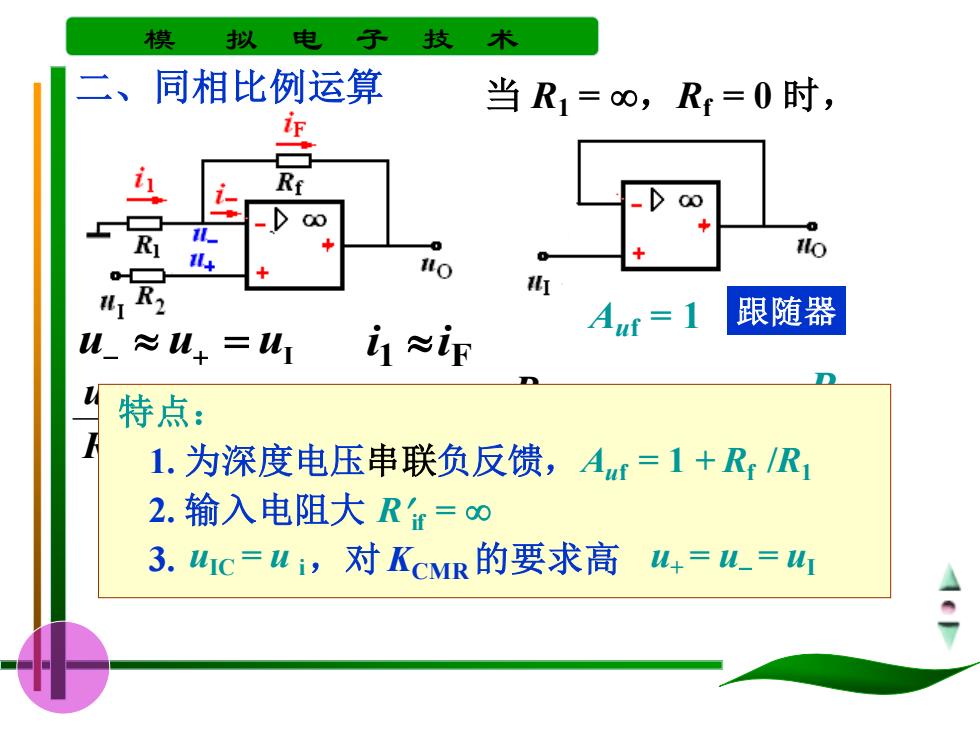
模 拟 电 子 技 术 二、 同相比例运算 当R1=o,R=0时, p 00 1R2 跟随器 ≈儿+ i~i Auf=1 特点: 1.为深度电压串联负反馈,Aut=1+RR1 2.输入电阻大Rr=0 3.1c=Wi,对KCMR的要求高 +=_=
模 拟 电 子 技 术 二、同相比例运算 u− u+ = uI 1 F i i , f O I 1 I R u u R u − = I 1 f O (1 )u R R u = + 1 f f 1 R R Au = + Auf = 1 跟随器 当 R1 = ,Rf = 0 时, 特点: 1. 为深度电压串联负反馈,Auf = 1 + Rf /R1 2. 输入电阻大 R if = 3. uIC = u i,对 KCMR 的要求高 u+ = u− = uI
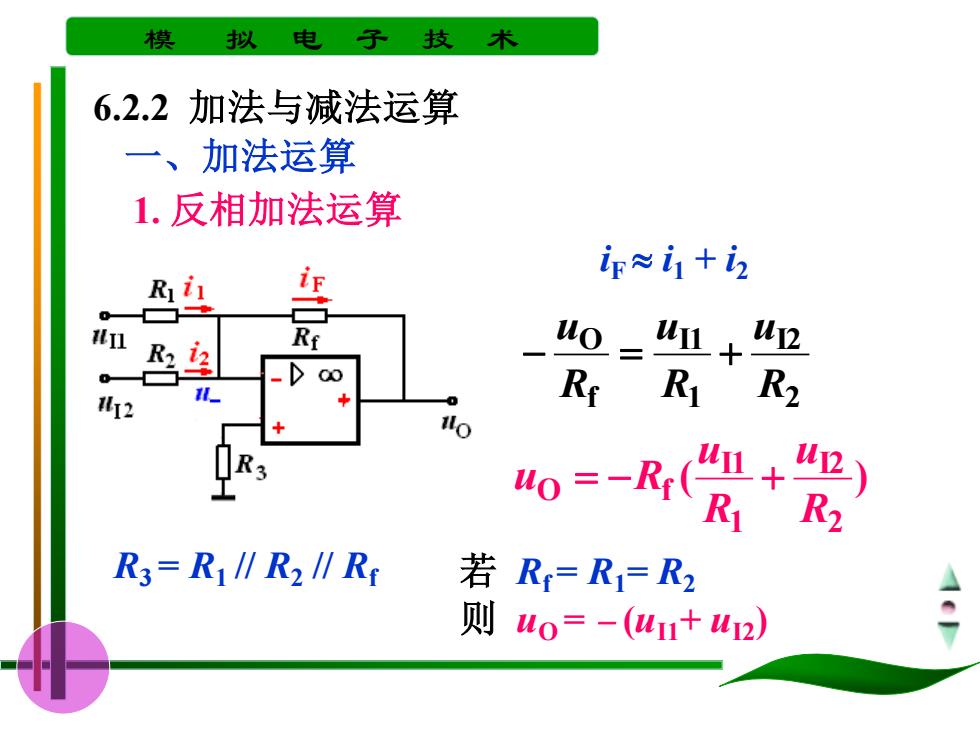
模 拟 电 子 技 6.2.2加法与减法运算 一、加法运算 1.反相加法运算 igi+i Ril Ri 40=41+42 _oo 12 l Ri RR2 + Wo=-RcRj R3=R1∥R2∥R 若R=R1=R2 则uo=-(u+u2)
模 拟 电 子 技 术 6.2.2 加法与减法运算 一、加法运算 1. 反相加法运算 R3 = R1 // R2 // Rf iF i1 + i2 2 I2 1 I1 f O R u R u R u − = + ( ) 2 I2 1 I1 O f R u R u u = −R + 若 Rf = R1= R2 则 uO = − (uI1+ uI2)
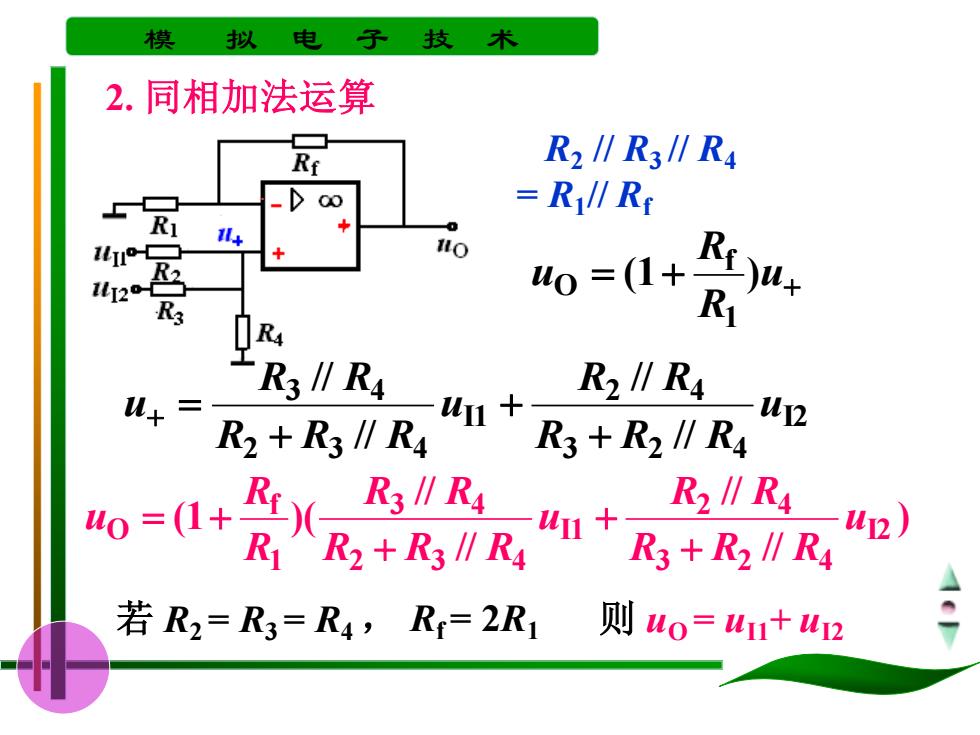
模 拟 电 子 技 术 2.同相加法运算 Ri R2∥R3∥R4 =R∥R R1 1+ 42 u0=(1+ R R3∥R4 R2∥R4 + 1 1+ W2 R2+R3∥R4 R3+R2∥R4 0=(1+ R3∥R4 1 R2∥R4 R1R2+R3∥R4 +R3+R∥R4 2) 若R2=R3=R4,Rr=2R1 则uo=4+W2
模 拟 电 子 技 术 R2 // R3 // R4 = R1 // Rf = + u+ R R u (1 ) 1 f O ) // // // // (1 )( I2 3 2 4 2 4 I1 2 3 4 3 4 1 f O u R R R R R u R R R R R R R u + + + = + I2 3 2 4 2 4 I1 2 3 4 3 4 // // // // u R R R R R u R R R R R u + + + + = 若 R2 = R3 = R4 , Rf = 2R1 则 uO = uI1+ uI2 2. 同相加法运算
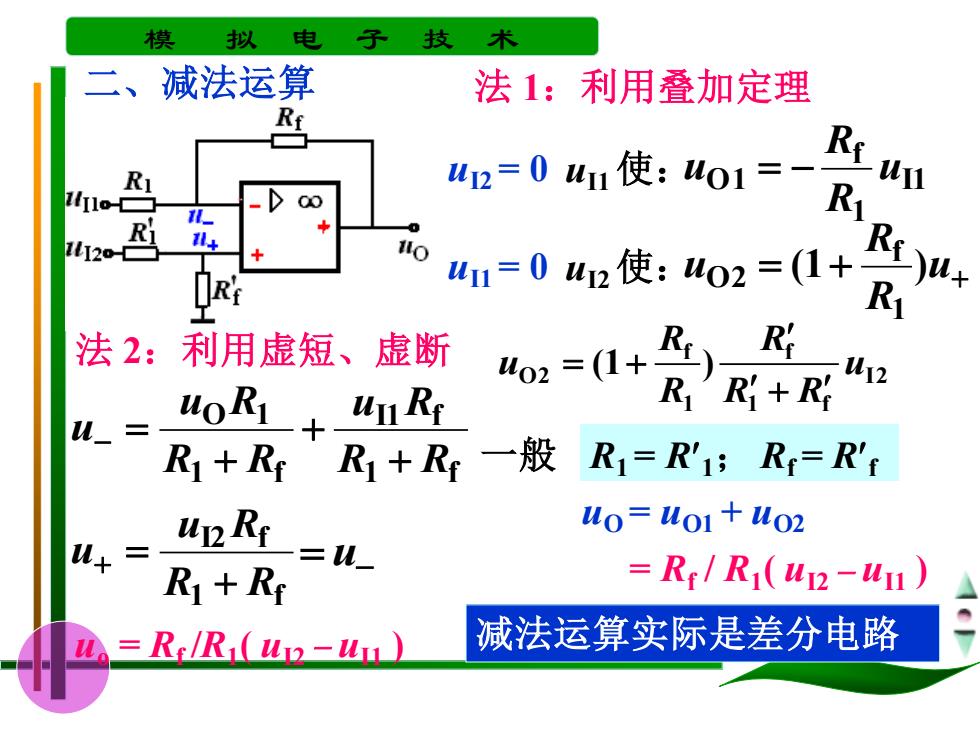
模 拟 电 子 技 术 二、 减法运算 法1:利用叠加定理 Ri 42=041使:4o1=- Riun l1- 中 ORi 4m=042使:uo2=(1+ R 法2:利用虚短、 虚断 402=(1+ Rt Rt uoRL+ uu Rt R Ri+R u R1+Rt R1+R一般 R1=R1;Rt=R't upRt uo=uoi+uo2 R1+Rt =Re/R1(u2-1) R:/R (up-u1) 减法运算实际是差分电路
模 拟 电 子 技 术 法 1:利用叠加定理 uI2 = 0 uI1 使: I1 1 f O 1 u R R u = − uI1 = 0 uI2 使: = + u+ R R u (1 ) 1 f O 2 I2 1 f f 1 f O2 (1 ) u R R R R R u + = + 一般 R1 = R 1; Rf = R f uO = uO1 + uO2 = Rf / R1 ( uI2 − uI1 ) 法 2:利用虚短、虚断 1 f I1 f 1 f O 1 R R u R R R u R u + + + − = 1 f I2 f R R u R u + + = = u− uo = Rf /R1 ( uI2 − uI1 ) 减法运算实际是差分电路 二、减法运算