
16.低通原型和滤波器原理 电路综合 西安电子科技大学,电子工程学院 苏诗置
16. 低通原型和滤波器原理 电路综合 西安电子科技大学,电子工程学院 苏 涛
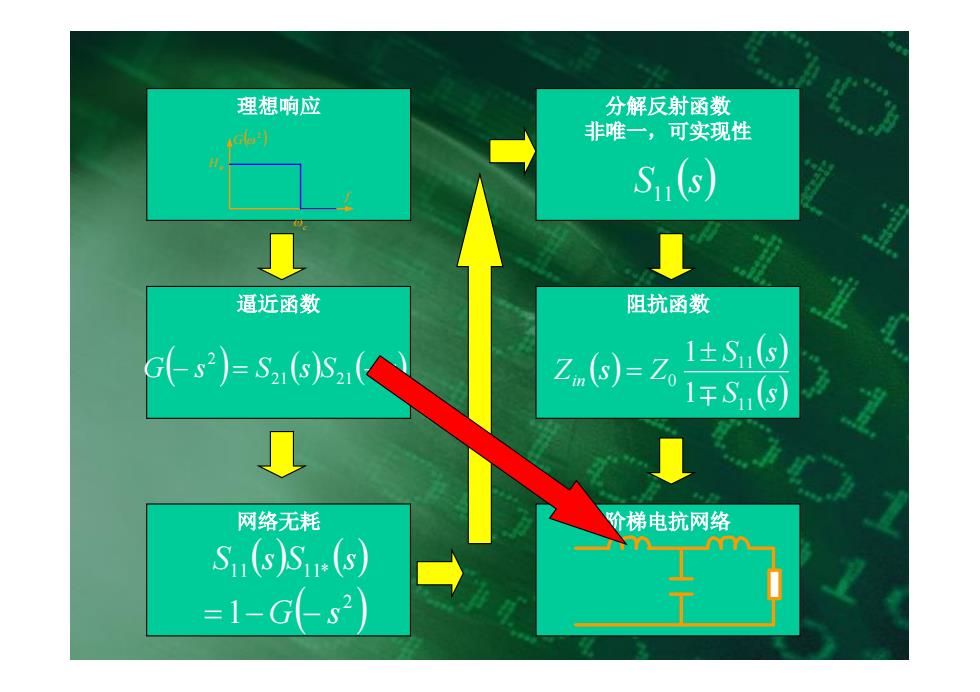
理想响应 分解反射函数 非唯一,可实现性 Ss) 逼近函数 阻抗函数 G-s2)=S2(5)S2i 2.6)=Z1年s0 ,1±S 1 网络无耗 阶梯电抗网络 SS)S.s) =1-Gs2)
理想响应 wc Hn f ( ) 2 G w 逼近函数 G(- s ) = S (s)S (- s) 21 21 2 网络无耗 ( ) ( ) ( ) 2 11 11* 1 G s S s S s = - - 分解反射函数 非唯一,可实现性 S (s) 11 阻抗函数 ( ) ( ) S ( )s S s Zin s Z 11 11 0 1 1 m ± = 阶梯电抗网络

16.低通原型和滤波器原理电路综合 一、 低通原型及元件值 二、阻抗变换和频率变换
16. 低通原型和滤波器原理电路综合 一、低通原型及元件值 二、阻抗变换和频率变换

16.低通原型和滤波器原理电路综合 低通原型及元件值 二、阻抗变换和频率变换 置
16. 低通原型和滤波器原理电路综合 一、低通原型及元件值 二、阻抗变换和频率变换
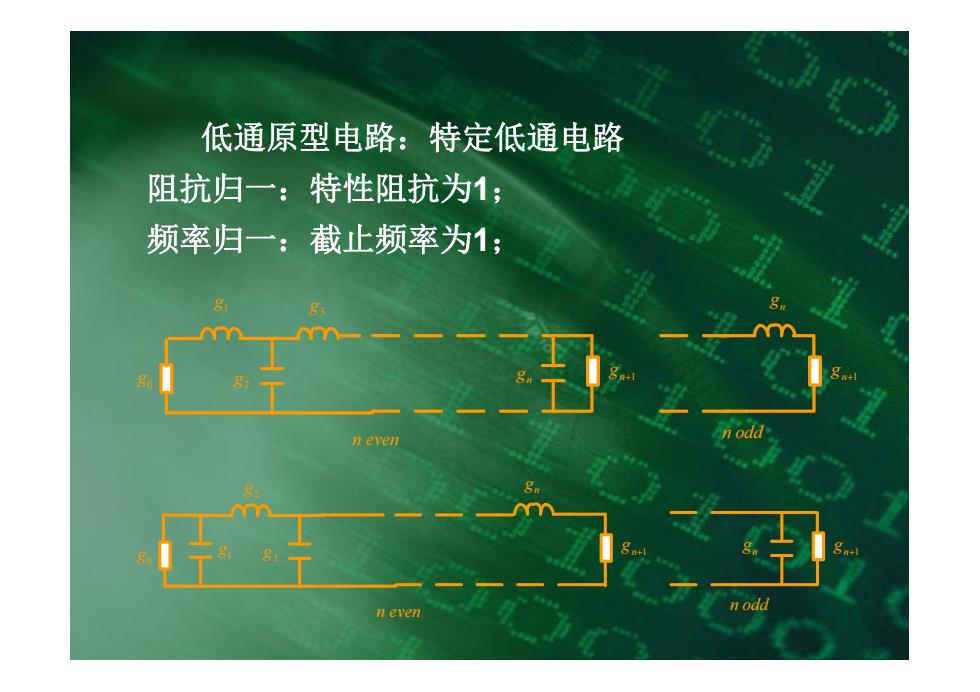
低通原型电路:特定低通电路 阻抗归一:特性阻抗为1; 频率归一:截止频率为1; n even nodd n even n odd
g1 g2 g3 n+1 g n g 0 g n+1 g n g n even n odd 低通原型电路:特定低通电路 阻抗归一:特性阻抗为1; 频率归一:截止频率为1; 1 g g2 3 g gn+1 n g 0 g gn gn+1 n even n odd

串联电感值 8klk=1.2.n 并联电容值 源电阻R,若g1三C 80= 道 源电导G6若g,=八 负载电阻R,若g,=C 负载电导G1,若gn=L 阻抗归一8。=1;频率归一
î í ì = = 并联电容值 串联电感值 k k n g 1,2,L î í ì ¢ = ¢ ¢ = ¢ = 0 1 1 0 1 1 0 , , G g L R g C g 源电导 若 源电阻 若 î í ì ¢ = ¢ ¢ = ¢ = + + + n n n n n n n G g L R g C g 负载电导 ,若 负载电阻 ,若 1 1 1 1 g0 = ¢ =1 阻抗归一 ;频率归一 wc

Butterworth低通原型的元件值 80=1.0 8x =2sin (2k-1m 2n ,k=1,2,n 8m1=1.0 AL 带外衰减:而=而,>1 1og100-1 n int LR>AL 2log@
Butterworth低通原型的元件值 1.0 g0 = ( ) k n n k gk , 1,2, , 2 2 1 2sin ú = L û ù ê ë é - = p 1.0 gn+1 = 带外衰减: = >1 w ws LB > AL 1 2log log 10 1 int 10 + ú ú ú ú ú û ù ê ê ê ê ê ë é ÷ ÷ ø ö ç ç è æ - = s AL n w

Chebyshev低通原型的元件值 8o=1.0 81-29 4akidk k=23.n gk=bk18k- 1,n odd 8Hl= neven
Chebyshev低通原型的元件值 1.0 g0 = g 1 1 2 a g = k n b g a a g k k k k k , 2,3, , 4 1 1 = 1 = L - - - ï î ï í ì ÷ ø ö ç è + = æ n even n odd gn , 4 coth 1 , 1 2 b

其中, B=In coth 17.37 y=sinh ax sin b =y2+sin2
其中, ÷ ø ö ç è æ = 17.37 ln coth LAr b ÷ ø ö ç è æ = 2n sinh b g ( ) k n n k ak , 1,2, , 2 2 1 sin ú = L û ù ê ë é - = p k n n k bk sin , 1,2, , 2 2 ÷ = L ø ö ç è æ = + p g

当0=@>1时,要求L,之L 其中L分贝波纹 8=V1010-1 -1 ch-i 1010 红 置 100 一1 n int +1 ch @
当 时,要求 , 其中 分贝波纹 = >1 w ws Ls > LAs LAr 10 1 10 = - LAr e 1 10 1 10 1 int 1 10 10 1 + ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ë é - - = - - s L L ch ch n Ar As w