
18.公比线带通滤波器 苏涛 西安电子科技大学,电子工程学院
18. 公比线带通滤波器 苏 涛 西安电子科技大学,电子工程学院

滤波器综合:Butterworth,Chebyshev:综合 →LC梯形网络(低通),易于集总元件实现 问题: 1、集总元件LC在微波频率下实现困难; 2、微波频率下,元件之间的距离(或连线)是不 可忽略的
滤波器综合:Butterworth,Chebyshev综合 à LC梯形网络(低通),易于集总元件实现 问题: 1、集总元件LC在微波频率下实现困难; 2、微波频率下,元件之间的距离(或连线)是不 可忽略的

·集总元件LC等效,分布元件(传输线、谐振腔 等); ·网络结构变换,利于微波结构实现()/K变换 器); 窄带的,近似的 比如:高阻抗短截线等效串联电感;低阻抗短截线 等效并联电容。 另外一种近似,另外一种研究思路
• 集总元件LC等效,分布元件(传输线、谐振腔 等); • 网络结构变换,利于微波结构实现(J/K变换 器); 窄带的,近似的 比如:高阻抗短截线等效串联电感;低阻抗短截线 等效并联电容。 另外一种近似,另外一种研究思路

公比线带通滤波器 ⊥.Richard变换 2.uroda恒等关系 3。公比线低通
公比线带通滤波器 1. Richard变换 2. Kuroda恒等关系 3. 公比线低通

公比线带通滤波器 ⊥.Richard变换 2.Kuroda恒等关系 3.公比线低通
公比线带通滤波器 1. Richard变换 2. Kuroda恒等关系 3. 公比线低通

P.Richard为了用开路或者短路的传输线段来 实现LC网络而引入变换 Q=tan Bl=tan 频率变量; Q分布频率变量;(distributed frequency)
P. Richard为了用开路或者短路的传输线段来 实现LC网络而引入变换 ÷ ÷ ø ö ç ç è æ W = = p v l l w tan b tan w ® W w 频率变量; W 分布频率变量;(distributed frequency)

若采用上述变换, 电感电抗 X三tan61三ja证 Z。=L,0=B1 短路短截线 电容电导 jB.=jCtan B1=jC Y=C,0=β1 开路短截线 电感和电容即开路或短路短截线
若采用上述变换, 电感电抗 jX L = jL tan b l = jW L Z = L,q = b l 0 短路短截线 电容电导 jBc = jC tan b l = jWC Y = C,q = b l 0 开路短截线 电感和电容即开路或短路短截线

【讨论】 L、Richardi变换的周期性 相速和频率无关,无色散的,TEM模传输线; 即,电长度与频率成正比: 0=0 对于低通原型,截止频率为1;使经过Richard 变换后,仍为1;即 2=1
【讨论】 1、Richard变换的周期性 相速和频率无关,无色散的,TEM模传输线; 即,电长度与频率成正比; c c w w q = q 对于低通原型,截止频率为 1;使经过Richard 变换后,仍为1;即 W=1

=1=tan 0 显然地, 8 在020 时,传输线长度为四分之一波 长,这里将发生衰减的极点。 注意:远离截止频率时,短截线的阻抗将不再与 原来的集总元件阻抗匹配。·
c c c w w w w q = W=1 = tan 显然地, 8 , 4 p l qc = l = 在 时,传输线长度为四分之一波 长,这里将发生衰减的极点。 注意:远离截止频率时,短截线的阻抗将不再与 原来的集总元件阻抗匹配。. w = 2wc
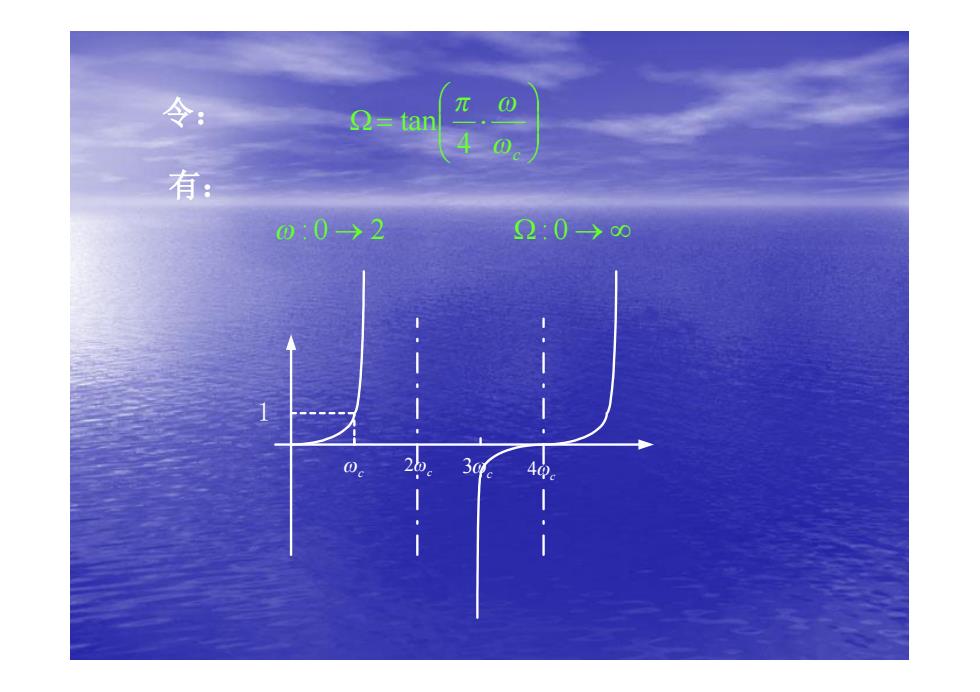
令: =tan 40 有: 00→2 Q0→00 1 c 2 3q. 40。 .i
令: ÷ ÷ ø ö ç ç è æ W= × wc p w 4 tan w : 0 ® 2 W : 0 ® ¥ 有: wc 2wc wc 4wc 3 1