西安电子科技大学：《数字信号处理》课程教学课件（讲稿）05 数字滤波器的基本概念及一些特殊滤波器

5.1数字滤波器的基本概念（1) ■数字滤波器： 口输入与输出均为数字信号 口通过一定数值运算 口改变输入信号所含频率成分的相对比例 口或者滤除某些频率成分 口或者进行信号检测与参数估计 口与模拟滤波的不同：信号的形式，滤波的方法 ■数字滤波器的实现方法： 口计算机软件 口专用数字信号处理芯片 口硬件（加法器、乘法器、延迟器)组合

5.1 数字滤波器的基本概念（1）  数字滤波器：  输入与输出均为数字信号  通过一定数值运算  改变输 信 所含频率 分的相 例 改变输入信号所含频率成分的相对比例  或者滤除某些频率成分  或者进行信号检测与参数估计  与模拟滤波的不同：信号的形式，滤波的方法  数字滤波器的实现方法：  计算机软件  专用数字信号处理芯片  硬件（加法器、乘法器、延迟器）组合 2  硬件（加法器、乘法器、延迟器）组合

5.1数字滤波器的基本概念(2) ■数字滤波器的可实现性 口因果稳定，系统传输函数的极点都在单位圆内 口实数乘法，系统函数的系数为实数，即零极点须共轭成 对出现，或者是实数 ■滤波器的种类—一 根据理论基础分 口经典滤波器（一般滤波器）：由线性系统构成 ■信号和干扰的频带互不重叠时采用 口现代滤波器：以随机信号处理理论为基础 ■例如：维纳滤波器、卡尔曼滤波器、自适应滤波器等 ■信号和干扰的频带相互重叠时采用

5.1 数字滤波器的基本概念（2）  数字滤波器的可实现性  因果稳定，系统传输函数的极点都在单位圆内  实数乘法，系统函数的系数为实数，即零极点须共轭成 对出现，或者是实数  滤波器的种类 —— 根据理论基础分  经典滤波器（一般滤波器）：由线性系统构成  信号和干扰的频带互不重叠时采用  现代滤波器：以随机信号处理理论为基础  例如：维纳滤波器、卡尔曼滤波器、自适应滤波器等 信号和 扰的频带相互重叠时采用 3  信号和干扰的频带相互重叠时采用

5.1数字滤波器的基本概念（3) ■经典滤波器 口功能划分：高通、低通、带通、带阻 口实现方法： ■无限脉冲响应数字滤波器一IlR,其h(n)为无限长，网络中有 反馈回路，系统函数为 2 H(z)= N( 1+∑azk D(2) k=1 ■有限脉冲响应数字滤波器一FIR N H(z)= ∑hn)z-” n=0 ■特殊滤波器： 口理想滤波器、一阶滤波器、二阶滤波器、数字谐振器、数字陷波 器、全通滤波器、最小相位滤波器、梳状滤波器、正弦波发生器。 g

5.1 数字滤波器的基本概念（3）  经典滤波器  功能划分：高通、低通、带通、带阻  实现方法：  无限脉冲响应数字滤波器 无限脉冲响应数字滤波器— IIR，其h(n)为无限长，网络中有 反馈回路，系统函数为 0 ( ) ( ) M r r r N b z N z H z       有限脉冲响应数字滤波器— FIR 1 ( ) ( ) 1 N k k k H z D z a z      有限脉冲响应数字滤波器— FIR 1 () () N n H z hnz      特殊滤波器：  理想滤波器、一阶滤波器、二阶滤波器、数字谐振器、数字陷波 n0 4  理想滤波器、 阶滤波器、 阶滤波器、数字谐振器、数字陷波 器、全通滤波器、最小相位滤波器、梳状滤波器、正弦波发生器

5.2理想数字滤波器 ■系统的无失真传输条件 口若信号ft)通过某系统后，响应为y()=Kf(t-td),则称该系 统为无失真传输系统。 f(t)一 h)=? y(t)=kf (t-ta) y(t)=kf(t-ta)=f(t)*h(t) ∴.h(t)=kδ(t-ta) ∴.H(U2)=ked 输出Y(U2)=|Y(j2e4@=kF(U2e,oe 幅频特性：Y(2)=kF(2) 理想模拟滤波器 相频特性：中，(2)=pr(2)-2ta 5

5.2理想数字滤波器  系统的无失真传输条件  若信号f( )t 通过某系统后，响应为y( ) f( t =K t-td )，则称该系 统为无失真传输系统。 f (t) h(t)  ? y(t)  kf (t  td ) y(t) kf (t t ) f (t)*h(t)   d   h(t)  k (t t ) ( ) d j t H j ke  ( ) ( )    d  h t  k t t ( ) j ( ) ( ) () () () Y f d j j j t Y j Y j e kF j e e       输出     幅频特性: Y j kF j () ()   理想模拟滤波器 5 () () yf d 相频特性:       t

5.2.1理想数字滤波器的特点及分类 ■特点： 口在滤波器的通带内，幅度为常数，在阻带中幅度为零 口具有线性相位； 口单位脉冲响应为非因果无限长序列 ■ 理想带通滤波器 口频率响应 H(e)= Cejo%0<o1ok02<π 0 其他o 口幅频特性 H(el)=C 相频特性p(o)=-on 口群时延 i(w)-dp(o) 输入信号所有频率分量的时间延迟相同 do 口输出信号的频率响应 Y(e)=X(e)H(e)o<o<o 口输出信号 y(n)=Cx(n-no) 6

5.2.1理想数字滤波器的特点及分类  特点：  在滤波器的通带内，幅度为常数，在阻带中幅度为零 在阻带中幅度为零  具有线性相位；  单位脉冲响应为非因果无限长序列  理想带通滤波器  频率响应 0 0 1 2 | | ( ) j n j Ce H            幅频特性 相频特性 | | ( ) 0 j H e     其他 ( ) j He C   0  幅频特性 相频特性 ( )     n  群时延 输入信号所有频率分量的时间延迟相同  输出信号的频率响应 He C ( ) 0 ( ) 0 ( ) ( ) g d n d        输出信号的频率响应  输出信号 1 2 ( ) ( )( ) j jj Ye Xe He         6  输出信号 0 y() ( ) n Cx n n  

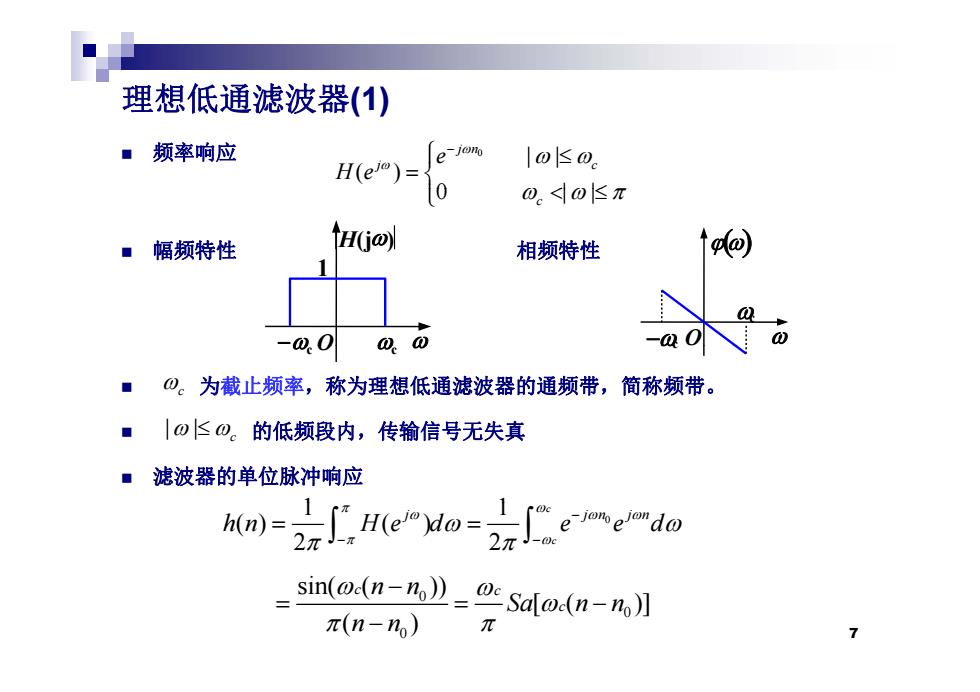
理想低通滤波器(1) ■频率响应 e-jon H(ej0)- |o≤0。 0。<0长π ■ 幅频特性 H(jo) 相频特性 po -00 @,0 -0 ■0。 为截止频率，称为理想低通滤波器的通频带，简称频带。 ■|⊙K⊙。的低频段内，传输信号无失真 ■滤波器的单位脉冲响应 sim(o.(n-n》_OSa[o(n-n)】 π(n-n)

理想低通滤波器( ) 1  频率响应 0 | | ( ) 0 || j n j c e H e               幅频特性 相频特性 0 ||    c   H(j) 1     O   1 O  c c  为截止频率，称为理想低通滤波器的通频带，简称频带。 的低频段内 传输信号无失真 c O c  c c  | | 的低频段内，传输信号无失真  滤波器的单位脉冲响应 | |  c 1 1 0 () ( ) 2 2 c c j jn j n hn He d e e d                   i ( ( )) 7 0 0 0 sin( ( )) [ ( )] ( ) c c c n n Sa n n n n         

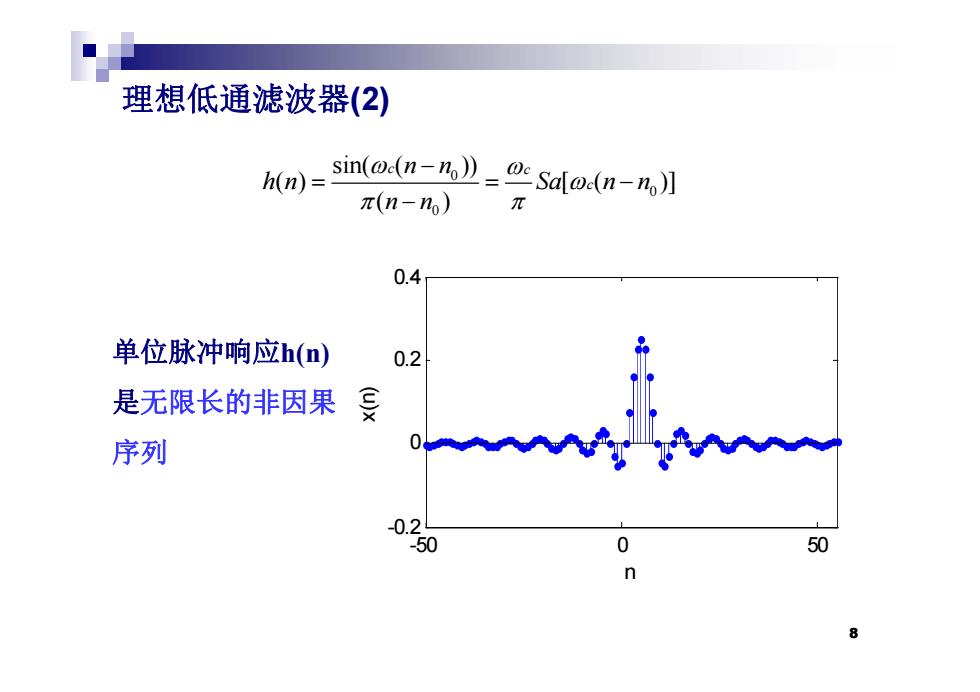
理想低通滤波器(2) h(n) sin(o.n-》_Saw(n-n】 π(n-n) π 0.4 单位脉冲响应h(n) 0.2 是无限长的非因果曼 序列 -0.2 50 0 50

理想低通滤波器( ) 2 0 0 sin( ( )) ( ) [ ( )] c c c n n h n Sa n n        0 0 ( ) [ ( )] ( ) h n Sa n n c n n     0.4 单位脉冲响应h( ) 0.2 x(n) h(n) 是无限长的非因果 序列 0 -50 0 50 -0.2 n 8

理想滤波器 H(e) H(e) π 2n 低通 高通 in.n. H(e) H(e) 2 2 π 2元 带通 带阻 9

理想滤波器 ( ) j H  e ( ) j H e   2  0  2  0 ( ) j H e  ( ) j H e  低通 高通   2  0 0  2  带通 带阻 9

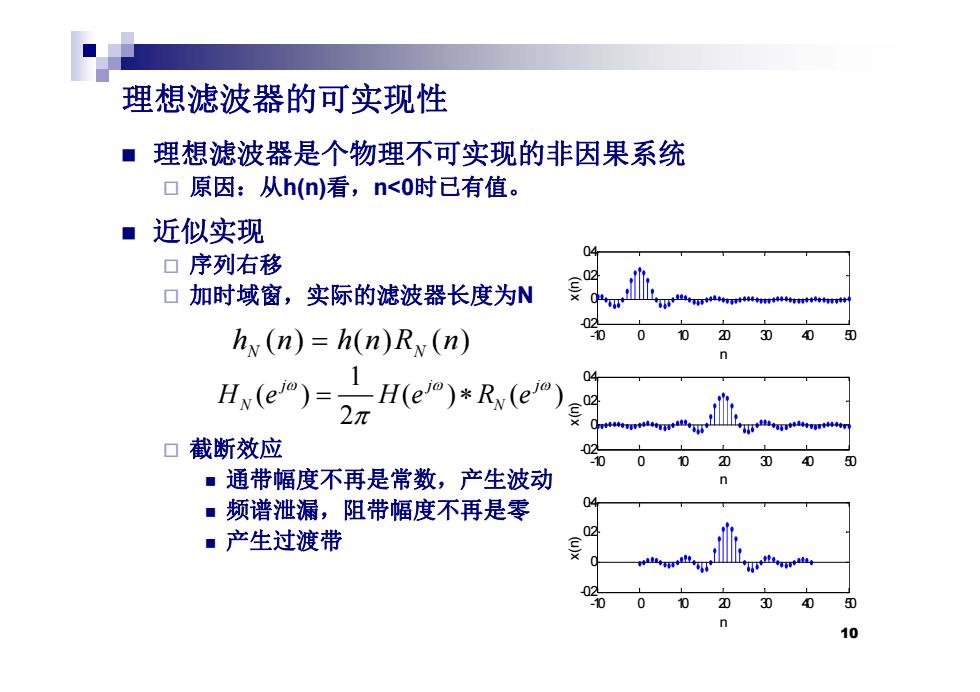
理想滤波器的可实现性 理想滤波器是个物理不可实现的非因果系统 口原因：从h(n)看，n<0时已有值。 ■近似实现 口序列右移 口加时域窗，实际的滤波器长度为N 02 hx (n)=h(n)Rx (n) -10 0020304050 Hy()H()*Ry(e) 2元 口截断效应 002D 30 409 ■通带幅度不再是常数，产生波动 ■频谱泄漏，阻带幅度不再是零 ■产生过渡带 广a山Aoa -10 0102D040 50

理想滤波器的可实现性  理想滤波器是个物理不可实现的非因果系统  原因：从h(n) 看，n<0时已有值 。  近似实现  序列右移 0.4  加时域窗，实际的滤波器长度为 N () () () N N h n hnR n  -10 0 10 20 30 40 50 -0.2 0 0. 2 x(n) () () () N N h n hnR n 1 () () () 2 j jj H e He R e N N       n 0 0.2 0.4 x(n)  截断效应  通带幅度不再是常数，产生波动 频谱泄漏 阻带幅度不再是零  -10 0 10 20 30 40 50 -0.2 0 n x 04  频谱泄漏，阻带幅度不再是零  产生过渡带 0 0.2 0.4 x(n) 10 -10 0 10 20 30 40 50 -0.2 n

5.3简单滤波器设计 ■基于零极点配置的的简单滤波器设计方法 ■原理： 口极点靠近单位圆，频率响应的峰值越高；极点放在需加强的频率 点附近 口零点靠近单位圆，频率响应的谷值越小；零点放在需减弱的频率 点附近 口约束条件 ■极点在单位圆内，保证滤波器的因果稳定； ■零、极点须共轭成对，或者是实数，保证系统函数系数为实数。 1

5 3. 简单滤波器设计  基于零极点配置的的简单滤波器设计方法  原理：  极点靠近单位圆，频率响应的峰值越高；极点放在需加强的频率 点附近  零点靠近单位圆，频率响应的谷值越小；零点放在需减弱的频率 点附近  约束条件  极点在单位圆内，保证滤波器的因果稳定；  零、极点须共轭成对，或者是实数，保证系统函数系数为实数。 11