西安电子科技大学：《高等微波网络》课程教学课件（讲稿）22 General Chebyshev综合

22、General Chebyshev 滤波器设计 苏涛 西安电子科技大学，电子工程学院 710071

苏 涛 西安电子科技大学，电子工程学院 710071 22、General Chebyshev 滤波器设计

双工器 介质滤波器

双工器 介质滤波器

83 80Ma8 8影E8盟 士-688 1740.000 o MHz 3- 4-串盟 PRm con 8T:7gg8888 SPAN 25888888mm Passband Response

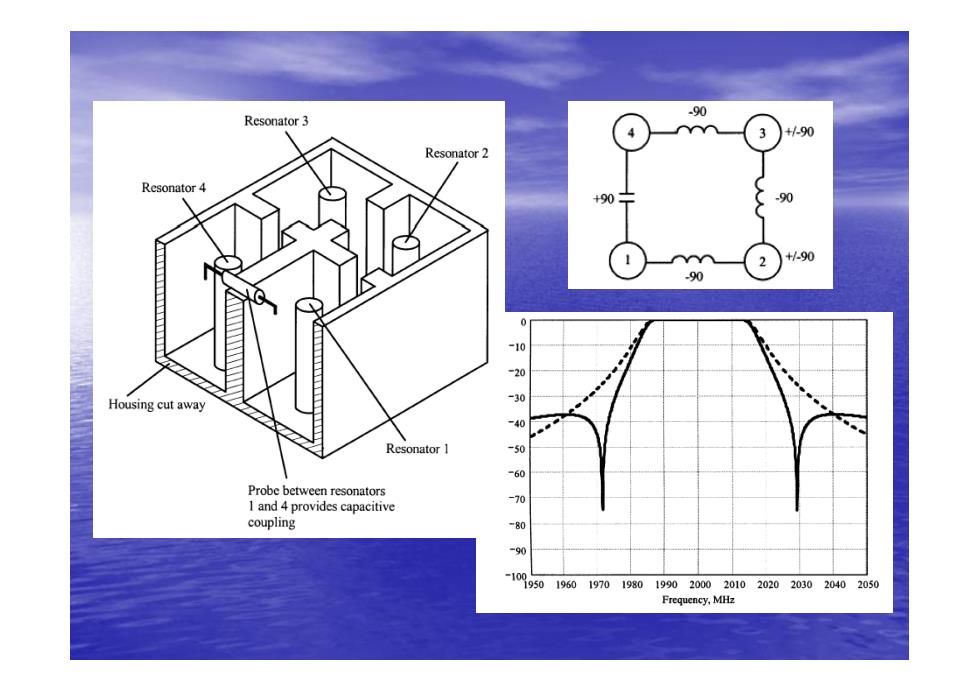
.90 Resonator 3 +/-90 Resonator 2 Resonator 4 +90 % 2 +/90 90 o -20 Housing cut away -30 -40 Resonator 1 Probe between resonators I and 4 provides capacitive -70 coupling -80 -90 -10o9501960197019801902020102020203020402050 Frequency,MHz

3 different solutions of the same 8-2-2 filter 1 》 12345573 113+)671 Matrix of the 1st Solution folded Matrix of the 2n4Solution Matrix of the 3rd solution 1st solution Signal flow graph 2m solution Signal flow graph 3rd solution Signal flow graph

Using the 7-3 filter from synthesis results Example of different solution for the same filter 123456 室 6 1st solution M Matrix 20 solution M Matrix 3d solution M Matrix 0.48353 60.79377 0.53363 0.5377.3 07970 50.970 0222 281 0337 798 0.7970 0.4574 0,5220 0357 0.5050 0.3577 0.4910 361 361 0.4910 1st solution Signal flow graph 2nd solution Signal flow graph 3rd solution Signal flow graph

General Chebyshev综合 个.General Chebyshev函数和综合 2.耦合矩阵求解

General Chebyshev综合 1. General Chebyshev函数和综合 2. 耦合矩阵求解

General Chebyshev综合 L,General Chebyshev函数和综合 L.1 General Chebyshevi函数 1.2 General Chebyshev有理分式求解 1.3 General Chebyshev函数例子 2、耦合矩阵求解

General Chebyshev综合 1、General Chebyshev函数和综合 1.1 General Chebyshev函数 1.2 General Chebyshev有理分式求解 1.3 General Chebyshev函数例子 2、耦合矩阵求解

I.1 General Chebyshevi函数 对于任意的双口，耦合谐振腔网络，传输和反射 可以表示为N阶多项式的比值 S1(w)= FN(w) 52(w）= Px(w) EN(w) EEN(w) 其中，0是实数频率，对应的复频率拓展为s=j@ 等波纹系数为 1 Py(w) E= V10L/10-1 Fy(w) 上面的多项式已经归一化了，即其最高次项的系数为1

1.1 General Chebyshev函数 对于任意的双口，耦合谐振腔网络，传输和反射 可以表示为N阶多项式的比值 其中，w 是实数频率，对应的复频率拓展为 s = jw 等波纹系数为 上面的多项式已经归一化了，即其最高次项的系数为1

根据能量守恒定理 5悦+5强=1 1 1 5员)=1+2C(o =(1+jaCw(w)1-jCw(w》 CN(w)= FN(w) PN(w) Cv(w,称为N阶滤波函数，定义其为General Chebyshevi函数

根据能量守恒定理 称为N阶滤波函数，定义其为General Chebyshev函数