
24、总结 苏涛 西安电子科技大学,电子工程学院 710071
苏 涛 西安电子科技大学,电子工程学院 710071 24、总 结

总结 ·网络的思想 ·网络参数 ·网络分析 ·网络综合
总 结 • 网络的思想 • 网络参数 • 网络分析 • 网络综合

网络思想 黑箱 ·“黑箱”; ·功能网络,变换; ·分析、综合; ·波网络;
黑箱 • “黑箱” ; • 功能网络,变换; • 分析、综合; • 波网络; 网络思想
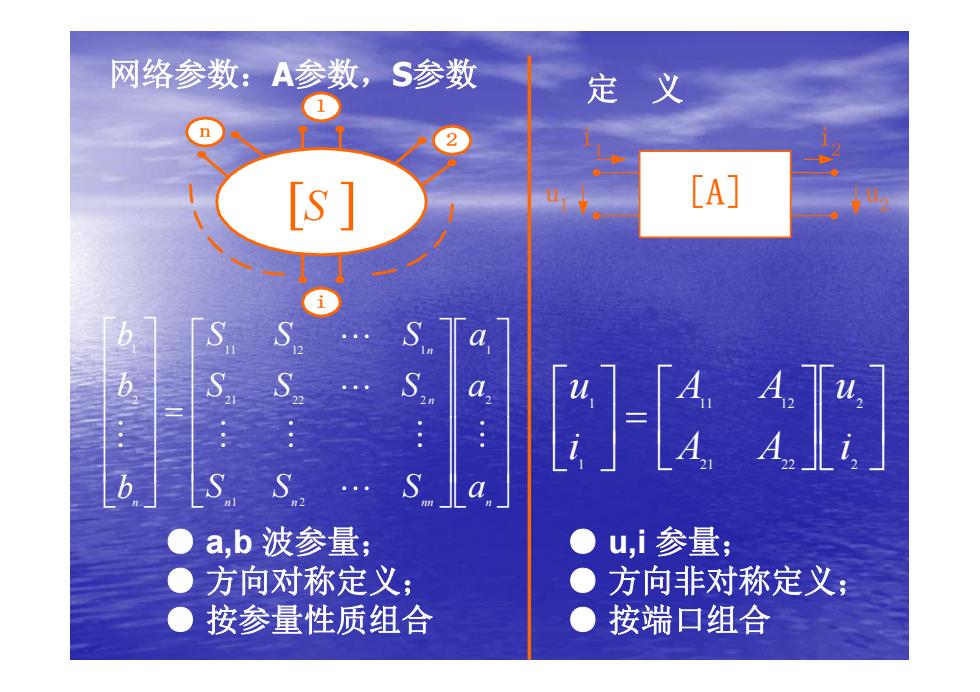
网络参数:A参数,S参数 定义 1 n 2 [s] [A] b S a 8l. a : S S S a a,b波参量; ●u,i参量; ● 方向对称定义: 方向非对称定义: 按参量性质组合 ● 按端口组合
网络参数:A参数,S参数 定 义 [A] i1 i2 u1 u2 ú û ù ê ë é ú û ù ê ë é =ú û ù ê ë é 2 2 21 22 11 12 1 1 i u A A A A i u ● u,i 参量; ● 方向非对称定义; ● 按端口组合 1 2 i n [S ] ú ú ú ú û ù ê ê ê ê ë é ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é n n nn n n n n a a a S S S S S S S S S b b b M L M M M L L M 2 1 1 2 21 22 2 11 12 1 2 1 ● a,b 波参量; ● 方向对称定义; ● 按参量性质组合

参数含义 b 2端口匹配时, 开路转移电压比 1端口自反射系数 u, =0 b 1端口匹配时, 开路转移导纳 a 2→1传输 m=0 2端口匹配时, 短路转移阻抗 a 1→2传输 1a=0 1端口匹配时, a 2端口自反射系数 i 短路转移电流比 a=0
参数含义 2 0 1 11 2 = = i u u A 开路转移电压比 2 0 1 12 2 = = i u i A 开路转移导纳 2 0 1 21 2 = = u i u A 短路转移阻抗 2 0 1 22 2 = = u i i A 短路转移电流比 1 0 1 11 2 = = a a b S 2端口匹配时, 1端口自反射系数 2 0 1 12 1= = a a b S 1端口匹配时, 2→1传输 1 0 2 21 2 = = a a b S 2端口匹配时, 1→2传输 2 0 2 22 1= = a a b S 1端口匹配时, 2端口自反射系数
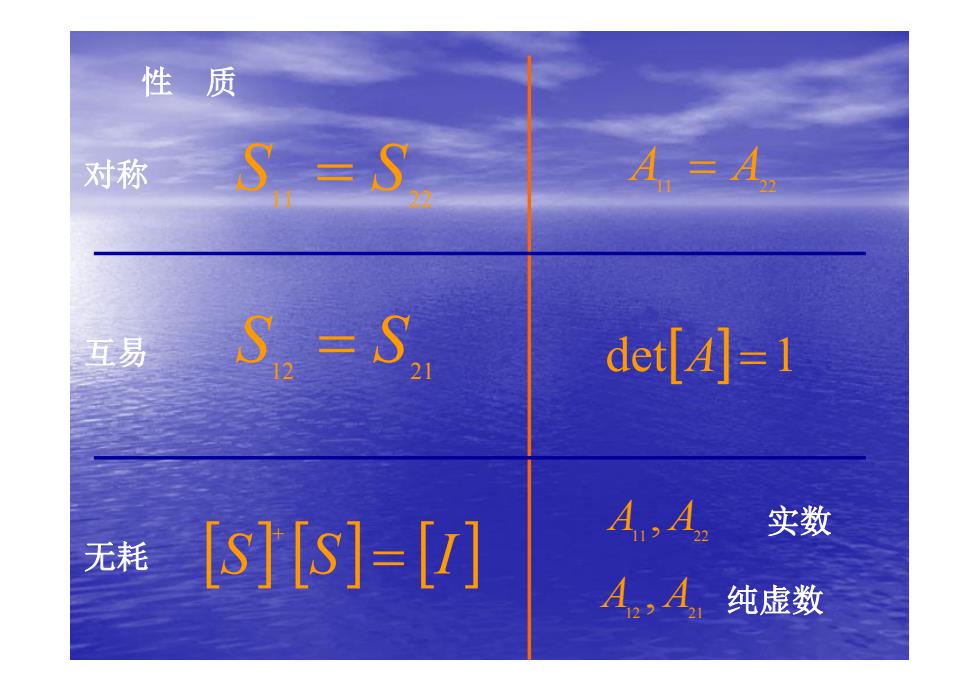
性质 对称 S A=4 互易 S.=S, det[4]=1 无耗 [s][s]=[] AA 实数 A,A纯虚数
性 质 对称 互易 det[A] =1 无耗 实数 12 21 A , A 纯虚数 A 11 = A 22 11 22 A , A 11 22 S = S 12 21 S = S [S] [S] = [I] +

定理 反射系数变换 阻抗变换 [S] [A] T=Su S2S2TL AZ.+4 1-S22TL AZ,+A
定 理 Z in [A] Z L 21 22 11 12 A Z A A Z A Z L L in + + = 反射系数变换 阻抗变换 [S] G L G in L L in S S S S - G G G = + 22 12 21 11 1
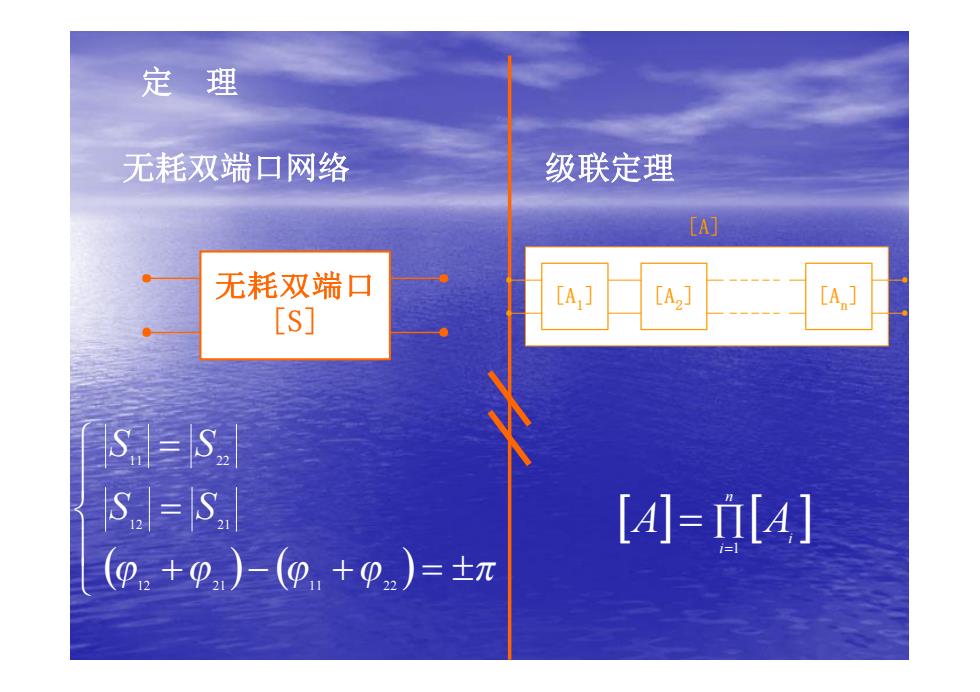
定理 无耗双端口网络 级联定理 [A] 无耗双端口 [A,] [A2] [A,] [S] S.=S. S.=s [4=[4] 0。+p,)-(0+0)=±元
定 理 [A1 ] [A2 ] [An ] [A] [ ] Õ[ ] = = n i A A i 1 无耗双端口网络 级联定理 ( ) ( ) ï î ï í ì + - + = ± = = j12 j21 j11 j22 p 12 21 11 22 S S S S 无耗双端口 [S]

定理 二端口无耗网络匹配定理 S=T 三端口无耗互易网络,三端口不能同时匹配; 四端口网络,耦合/隔离/匹配的关系; 注:S参数是波参数,直指波的传输和反射
定 理 • 二端口无耗网络匹配定理 • 三端口无耗互易网络,三端口不能同时匹配; • 四端口网络,耦合/隔离/匹配的关系; * 22 L S = G 注:S参数是波参数,直指波的传输和反射

广义散射参数是指对广义下各种电路都适用的,即不论电 路是时谐的还是非时谐的,也不论电路是集总参数的还是分布 参数的,都能适用的一种散射参数。它实际上是将常用的散射 参数推广引用于非时谐集总参数电路的结果。 ·非时谐,时谐: ·集总,分布; 时谐集总参数网络,同样存在入射和反射问题;仅仅是因 为集总电路分析时,电压和电流参量是入射和反射的叠加量, 没有直观反映反射。 集总参数网络没有传输线,没有特性阻抗
广义散射参数是指对广义下各种电路都适用的,即不论电 路是时谐的还是非时谐的,也不论电路是集总参数的还是分布 参数的,都能适用的一种散射参数。它实际上是将常用的散射 参数推广引用于非时谐集总参数电路的结果。 • 非时谐,时谐; • 集总,分布; 时谐集总参数网络,同样存在入射和反射问题;仅仅是因 为集总电路分析时,电压和电流参量是入射和反射的叠加量, 没有直观反映反射。 集总参数网络没有传输线,没有特性阻抗