
11.对称网络和奇偶模法 西安电子科技大学,电子工程学院 苏涛
11. 对称网络和奇偶模法 西安电子科技大学,电子工程学院 苏 涛

11.对称网络和奇偶模法 1.双端口对称网络 2.多端口对称网络 3.多对称性网络
11. 对称网络和奇偶模法 1. 双端口对称网络 2. 多端口对称网络 3. 多对称性网络

11.对称网络和奇偶模法 1,.双端口对称网络 ①S矩阵表示 ②Y矩阵表示 ⑧ 奇偶模与对称矩阵、,本征值的关系 ④奇偶模与坐标旋转 固实例 2.多端口对称网络 3.多对称性网络
11. 对称网络和奇偶模法 1. 双端口对称网络 ① S矩阵表示 ② Y矩阵表示 ③ 奇偶模与对称矩阵、本征值的关系 ④ 奇偶模与坐标旋转 ⑤ 实例 2. 多端口对称网络 3. 多对称性网络
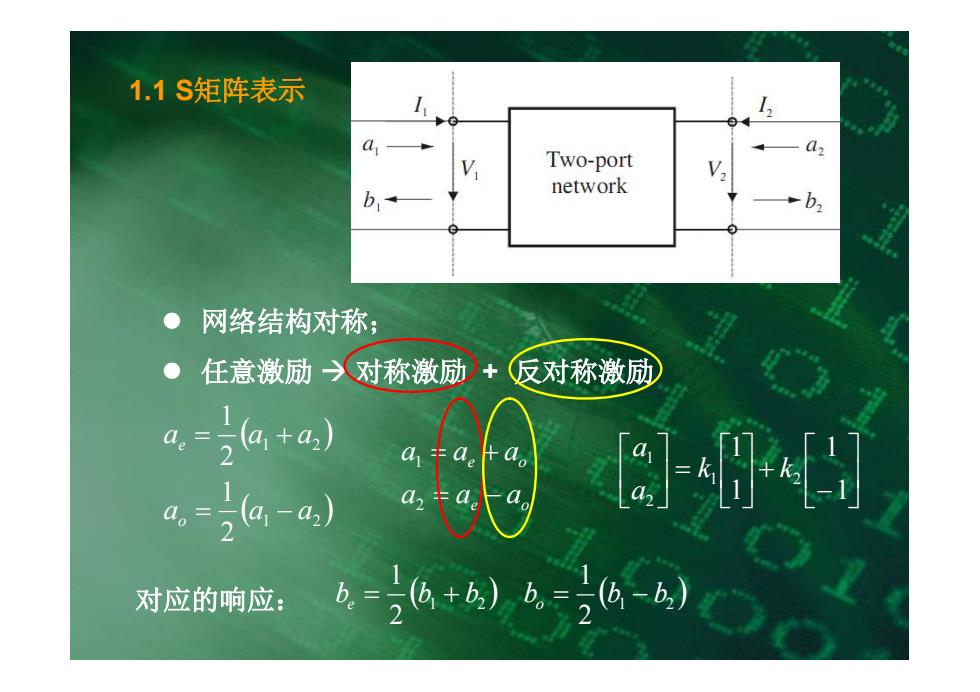
1.1S矩阵表示 a Two-port network b b2 网络结构对称; ●任意激励对称激励)+反对称激励 a-j(ata.) 2 a1 =ae a。 a。=2(4-a2) ka。 对应的响应: be= 6+) b。=2(6-b,)
l 网络结构对称; l 任意激励 à 对称激励 + 反对称激励 ( ) ( ) 1 2 1 2 2 1 2 1 a a a a a a o e = - = + e o e o a a a a a a = - = + 2 1 ú û ù ê ë é - +ú û ù ê ë é =ú û ù ê ë é 1 1 1 1 1 2 2 1 k k a a 对应的响应: ( ) ( ) 1 2 1 2 2 1 2 1 be = b + b bo = b - b 1.1 S矩阵表示
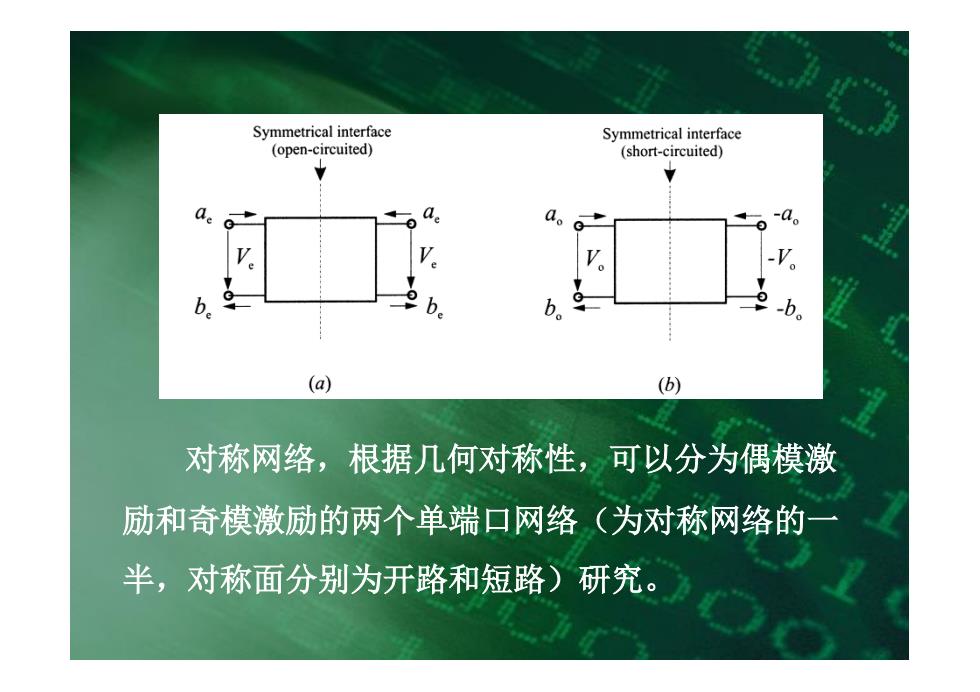
Symmetrical interface Symmetrical interface (open-circuited) (short-circuited) ae 0 0 -a。 V % b. b. b。 (a) (b) 对称网络,根据几何对称性,可以分为偶模激 励和奇模激励的两个单端口网络(为对称网络的一 半,对称面分别为开路和短路)研究
对称网络,根据几何对称性,可以分为偶模激 励和奇模激励的两个单端口网络(为对称网络的一 半,对称面分别为开路和短路)研究
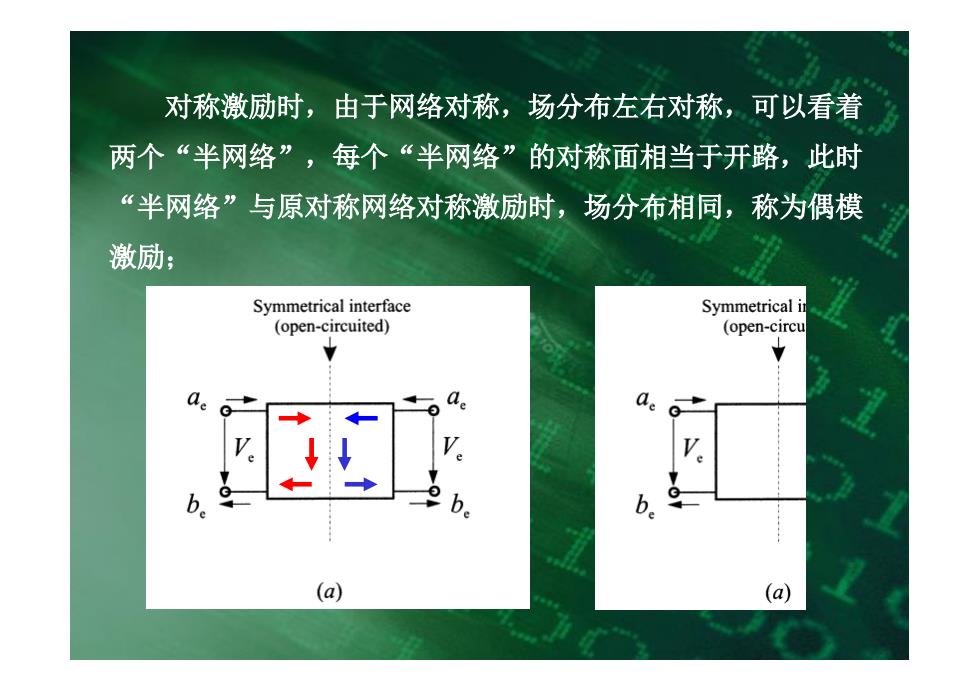
对称激励时,由于网络对称,场分布左右对称,可以看着 两个“半网络”,每个“半网络”的对称面相当于开路,此时 “半网络”与原对称网络对称激励时,场分布相同,称为偶模 激励; Symmetrical interface Symmetrical in (open-circuited) (open-circu 0 a a. Q V b (a) (a)
对称激励时,由于网络对称,场分布左右对称,可以看着 两个“半网络”,每个“半网络”的对称面相当于开路,此时 “半网络”与原对称网络对称激励时,场分布相同,称为偶模 激励;
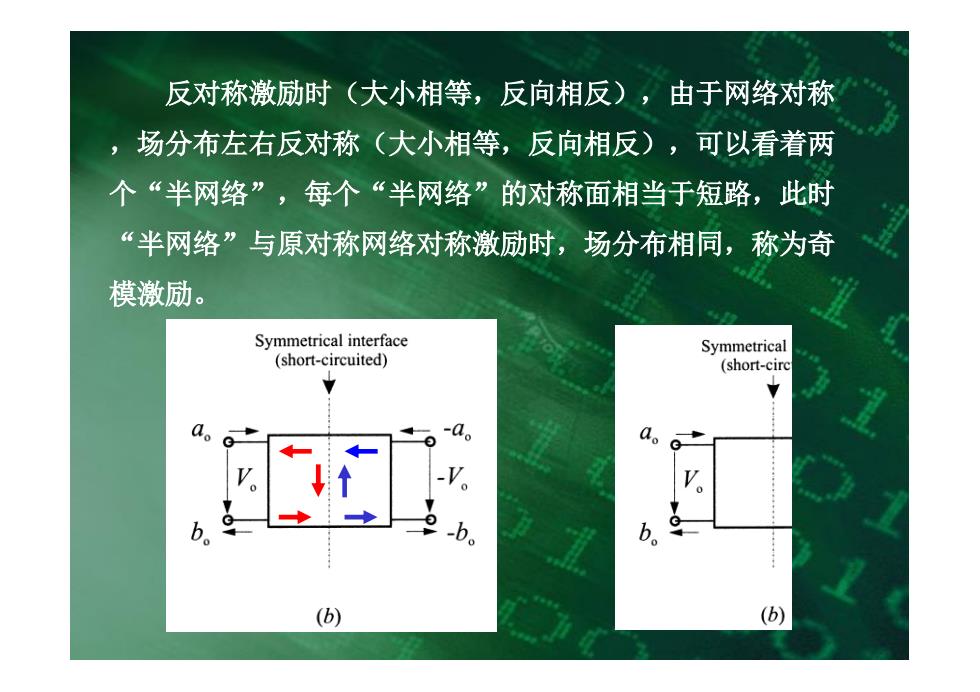
反对称激励时(大小相等,反向相反),由于网络对称 ,场分布左右反对称(大小相等,反向相反),可以看着两 个“半网络”,每个“半网络”的对称面相当于短路,此时 “半网络”与原对称网络对称激励时,场分布相同,称为奇 模激励。 4 Symmetrical interface Symmetrical (short-circuited) (short-circ Y 0 V b b b (b) (b)
反对称激励时(大小相等,反向相反),由于网络对称 ,场分布左右反对称(大小相等,反向相反),可以看着两 个“半网络”,每个“半网络”的对称面相当于短路,此时 “半网络”与原对称网络对称激励时,场分布相同,称为奇 模激励

任意激励可以看着是偶模激励和奇模激励的叠 加,则对称网络的网络参数可以有奇偶模反射系数 得到。 be 偶模反射系数 ae bo S11o= ao 奇模反射系数
任意激励可以看着是偶模激励和奇模激励的叠 加,则对称网络的网络参数可以有奇偶模反射系数 得到。 偶模反射系数 奇模反射系数

&'图 品 2-0 (Sne+Suo a1a2=0 2S1e-S1o) S22=S11 S12=S21
ú û ù ê ë é ú û ù ê ë é - + + - = ú û ù ê ë é ú û ù ê ë é - × ú û ù ê ë é ú û ù ê ë é - = ú û ù ê ë é ú û ù ê ë é ú û ù ê ë é - =ú û ù ê ë é ú û ù ê ë é - =ú û ù ê ë é 2 1 11 11 11 11 11 11 11 11 2 1 11 11 11 11 2 1 2 1 1 1 1 1 2 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 a a S S S S S S S S a a S S a a S S b b b b e o e o e o e o o e o e o e o e

Zime-Zo and Zine+Zol S11o= Zino-Zo1 Zino+Zol Zme Zino-Zi Yo-Yine Yino S1=S2=亿c+Zo(Zm+Zi) (Yo1+Yine)(YoI+Yino) S21=S12= Zine Zo-ZinoZo YinoYo-YineYo (Zine+Zo)(Zino +Zo1) (Yo1+Yine)(Yo1 +Yino) 上式使用奇偶模阻抗表示对称网络的S参数。>
上式使用奇偶模阻抗表示对称网络的S参数