
14.Butterworth综合 西安电子科技大学,电子工程学院
14. Butterworth 综 合 西安电子科技大学,电子工程学院 苏 涛
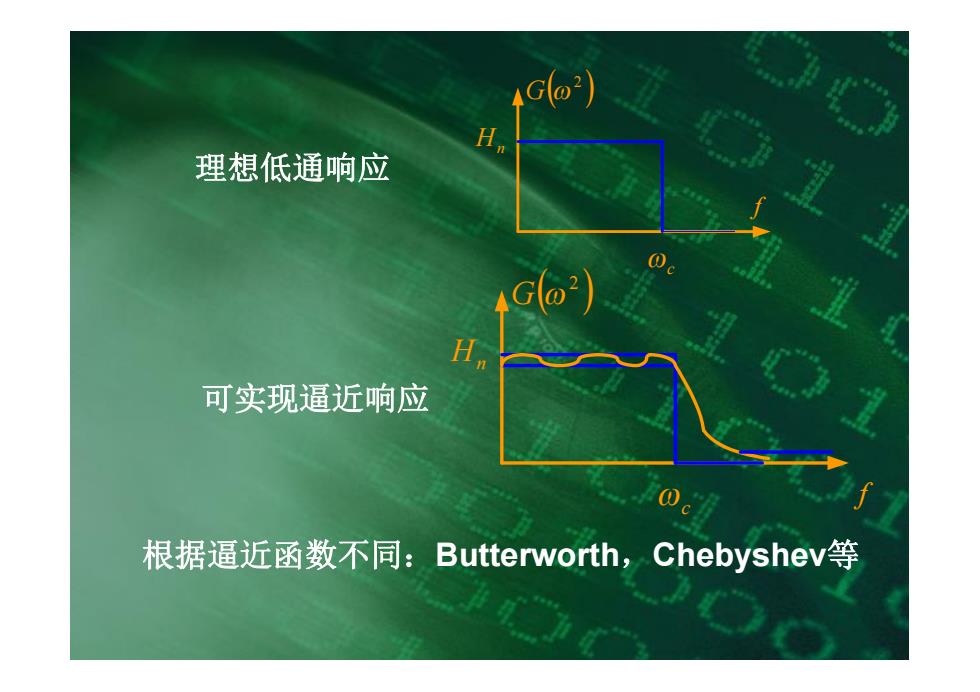
H 理想低通响应 H 可实现逼近响应 e 根据逼近函数不同:Butterworth,Chebyshev等
wc Hn f ( ) 2 G w 理想低通响应 wc Hn f ( ) 2 G w 可实现逼近响应 根据逼近函数不同:Butterworth,Chebyshev等

14.Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合
14. Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合

14.Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合
14. Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合

采用下面的函数逼近理想低通响应, Butterworth逼近 Go2)= 1+ G 置 H/2 n=3 c
( ) n c Hn G 2 2 1 ÷ ÷ ø ö ç ç è æ + = w w w 采用下面的函数逼近理想低通响应, —— Butterworth逼近 G f wc Hn Hn 2 n = 3 n = 5

1.3dB特性 当0=0。 时 G Glo)-2 置 H, H,/2 n=5 2.偶函数特性
1. 3dB特性 当 w =wc 时, ( ) 2 2 Hn G w = 2. 偶函数特性 G f wc Hn Hn 2 n = 3 n = 5

3,最大平滑特性 当而=0/0。<1时, 显然,在0=0处的1,2,一 2n-1阶导 数为
3. 最大平滑特性 当 w =w wc <1 时, ( ) = ( - + - +L) + = n n n n n n H H G 2 4 6 2 2 1 1 w w w w w 显然,在 处的1,2,——,2n-1阶导 数为零 w = 0

当可=0时,令而=1 Go2) H 1* 1+o” =Hn2m-04-6m+ 显然,在。=06=处的1,2厂 2n-1 阶导数为零 Butterworth逼近函数在零点和无穷远点均 具有最大平滑特性
显然,在 处的1,2,——,2n-1 阶导数为零 w¢ = 0 (w = ¥) Butterworth逼近函数在零点和无穷远点均 具有最大平滑特性 当 w = ¥ 时,令 w w 1 ¢ = ( ) = ( ¢ - ¢ - ¢ +L) + ¢ ¢ = ÷ ø ö ç è æ ¢ + = n n n n n n n n n H H H G 2 4 6 2 2 2 2 1 1 1 w w w w w w w

14.Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合
14. Butterworth综合 一、Butterworth逼近 二、Butterworth多项式 三、Butterworth多项式的n 四、Butterworth综合

Butterworth逼近 Go)-1+ Hn 复延拓 5=j而 西=一下 =(ys”3 c H.方
( ) n Hn G 2 2 1 w w + = Butterworth逼近 复延拓 s = jw w = - js 2 2 w = -s ( ) n n n s 2 2 w = -1 ( ) ( ) n n n s H G s 2 2 1+ -1 - =