
I.概述 西安电子科技大学,电子工程学院
Ⅰ. 概述 西安电子科技大学,电子工程学院 苏 涛

I.概述 一、 网络思想和概念 二、线性网络的语言一一矩阵 三、网络的内容和对象 置 四、波网络的特点
I. 概述 一、网络思想和概念 二、线性网络的语言——矩阵 三、网络的内容和对象 四、波网络的特点

I.概述 、 网络思想和概念 1、网络的思想和方法 2、网络方法比较 3、,网络的特征 二、线性网络的语言一一矩阵 三、网络的内容和对象 四、波网络的特点
I. 概述 一、网络思想和概念 1、网络的思想和方法 2、网络方法比较 3、网络的特征 二、线性网络的语言——矩阵 三、网络的内容和对象 四、波网络的特点

1、网络的思想方法 究事物,将其作为一个整个 一一“黑箱” 黑箱 什么啊? 00
1、网络的思想方法 研究事物,将其作为一个整体 ——“黑箱” 黑箱 什么啊?

个事物看不见、摸不着,对光没有反应, 对电没有反应,对磁没有反应,对 怎么证明它的存在? 事物必须有表现,有作用,才有意义,也才 可以被研究和利用 小学语文第15课《画风》,要求学生如何画风 几片叶子在风里飘动 放风筝 花儿在摇摆 少女的长发在风里飞 羽毛飘落 水波粼粼
一个事物看不见、摸不着,对光没有反应, 对电没有反应,对磁没有反应 ,对 . 怎么证明它的存在? 事物必须有表现,有作用,才有意义,也才 可以被研究和利用 小学语文第15课《画风》,要求学生如何画风 几片叶子在风里飘动 放风筝 花儿在摇摆 少女的长发在风里飞 羽毛飘落 水波粼粼

在网络思想中,把“黑箱”作为整体,对内部的 作用不研究,仅仅关心其对外的作用,并且通常把这 些对外的作用抽象到特定的区域或位置,称对外作用 的区域为端口 网络通过“端口”对外作用 黑箱
在网络思想中,把“黑箱”作为整体,对内部的 作用不研究,仅仅关心其对外的作用,并且通常把这 些对外的作用抽象到特定的区域或位置,称对外作用 的区域为端口 —— 网络通过“端口”对外作用 黑箱

通常人们总是关心在特定端口施加什么样的“输 入”,在特定的端口可以得到什么样的“输出”, 一网络注重“功能” 网络特性确定了各个端口物理量之间的关系 首先要确定端口上要研究的物理参量,比如:电 压、电流等;然后,要确定各个参量之间的关系;对 于每个端口有多个变量的情况,各个变量相互作用, 可能比较复杂
通常人们总是关心在特定端口施加什么样的“输 入” ,在特定的端口可以得到什么样的“输出” , —— 网络注重“功能” —— 网络特性确定了各个端口物理量之间的关系 首先要确定端口上要研究的物理参量,比如:电 压、电流等;然后,要确定各个参量之间的关系;对 于每个端口有多个变量的情况,各个变量相互作用, 可能比较复杂

2端口网络 a1, 比如:2端口网络,每个端口考察a和b两个物理 量,网络参数就是各个物理量之间的函数关系 lab]-f(az,bD larb2J=h(az,b) [4,a2]=g6,b2D
比如:2端口网络,每个端口考察a和b两个物理 量,网络参数就是各个物理量之间的函数关系 1 2 a1 ,b1 a2 ,b2 2 端口网络 [ ] ([ ]) 1 1 2 2 a ,b = f a ,b [ ] ([ ]) 1 2 1 2 a , a = g b ,b [ ] ([ ]) 1 2 2 1 a ,b = h a ,b
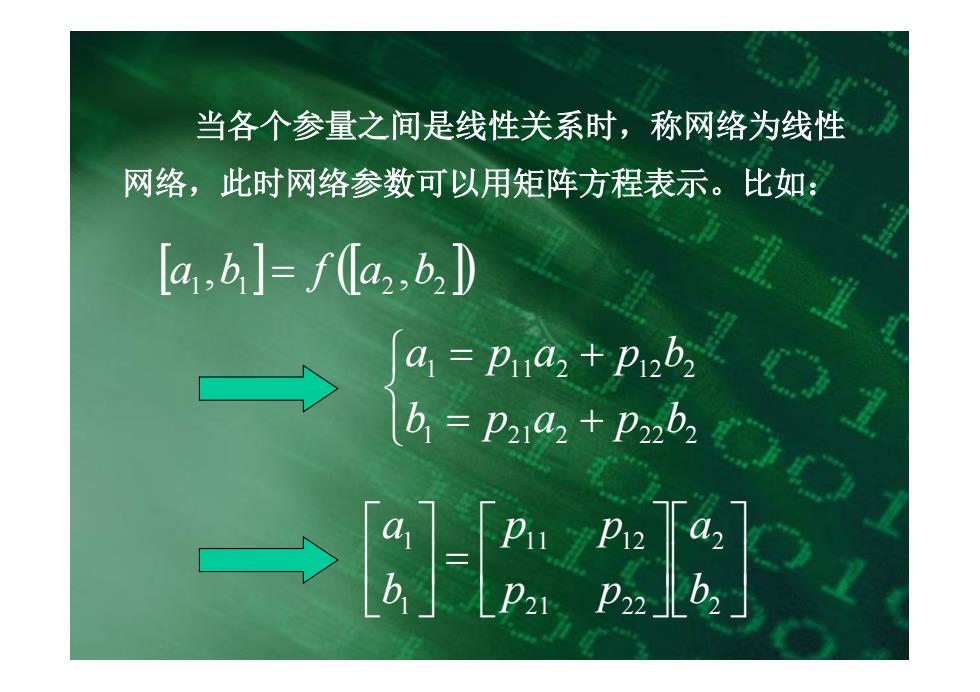
当各个参量之间是线性关系时,称网络为线性 网络,此时网络参数可以用矩阵方程表示。比如: [4,b]=f[a2,b,D d=Prdpb by=P22+p2zb2 卫12 p22
当各个参量之间是线性关系时,称网络为线性 网络,此时网络参数可以用矩阵方程表示。比如: [ ] ([ ]) 1 1 2 2 a ,b = f a ,b î í ì = + = + 1 21 2 22 2 1 11 2 12 2 b p a p b a p a p b ú û ù ê ë é ú û ù ê ë é =ú û ù ê ë é 2 2 21 22 11 12 1 1 b a p p p p b a

确定网络各个参量之间的关系,即求解网络方 程,通常有三种方法: 一是深入网络的内部,进行分析求解,得到网络参 数,称为本证的方法; 二是通过实验的方法,由多组对应参量,计算得到 网络参数; 三是大的网络由小网络连接而成,已知各个小网络 的参数及其相互连接状态,求解得到大网络参数; 网络参数有网络本身决定,通过端口数据可以 计算得到
确定网络各个参量之间的关系,即求解网络方 程,通常有三种方法: 一 是深入网络的内部,进行分析求解,得到网络参 数,称为本证的方法; 二 是通过实验的方法,由多组对应参量,计算得到 网络参数; 三 是大的网络由小网络连接而成,已知各个小网络 的参数及其相互连接状态,求解得到大网络参数; 网络参数有网络本身决定,通过端口数据可以 计算得到