
主要内容 ■线性相位FIR数字滤波器的特性 ■窗函数设计法(时间窗口法) ■频率取样法 ■R与FIR数字滤器的比较 2
主要内容 线性相位FIR数字滤波器的特性 窗函数设计法(时间窗口法) 频率取样法 IIR与FIR数字滤器的 较比 2

FIR数字滤波器的特点(与川R数字滤波器比较): ■优点: 口很容易获得严格的线性相位,避免被处理的信号产生 相位失真,这一特点在宽频带信号处理、阵列信号处 理、数据传输等系统中非常重要; 口极点全部在原点(永远稳定),无稳定性问题; 口任何一个非因果的有限长序列,总可以通过一定的延 时,转变为因果序列,所以因果性总是满足; 口无反馈运算,运算误差小
FIR数字滤波器的特点(与IIR数字滤波器比较 数字滤波器比较): 优点 : 很容易获得严格的线性相位,避免被处理的信号产生 相位失真,这 特点在宽频带信号处理 这一特点在宽频带信号处理、阵列信号处 理、数据传输等系统中非常重要; 极点全部在原点(永远稳定),无稳定性问题; 任何 个非因果的有限长序列 任何一个非因果的有限长序列,总可以通过 定的延 总可以通过一定的延 时,转变为因果序列, 所以因果性总是满足; 无反馈运算,运算误差小。 3

FIR数字滤波器的特点(与R数字滤波器比较): ■缺点: 口因为无极点,要获得好的过渡带特性,需以较高的阶 数为代价; 口无法利用模拟滤波器的设计结果,一般无解析设计公 式,要借助计算机辅助设计程序完成
FIR数字滤波器的特点(与IIR数字滤波器比较 数字滤波器比较): 缺点: 因为无极点,要获得好的过渡带特性,需以较高的阶 数为代价; 无法利用模拟滤波器的设计结果,一般无解析设计公 式,要借助计算机辅助设计程序完成。 4

FIR滤波器的设计方法 ■基于逼近理想滤波器特性的方法 口窗函数法 口频率采样法 口等波纹最佳逼近法 ■最优设计法
FIR滤波器的设计方法 基于逼近理想滤波器特性的方法 窗函数法 频率采样法 等波纹最佳 法 逼近 最优设计法 5

7.1线性相位F引R滤波器及其特性 ■线性相位系统的时域特性 ■线性相位系统的频域特性 ■线性相位系统H(z)的零点分布特性
7.1 线性相位FIR滤波器及其特性 线性相位系统的时域特性 7.1 线性相位FIR滤波器及其特性 线性相位系统的频域特性 线性相位系统H(z)的零点分布特性 6

1.FIR滤波器的定义 ■传输函数 N-I He)=-∑hln)e=H(o)eo, n=0 口幅度特性(可为负值)Hg(0) 与幅频响应不同 口相位特性 θ(0) .与相频响应不同 ■第一类线性相位FIRDR 口严格线性函数: 0(0)=-t0 ■第二类线性相位FIRDR 口满足: 0(0)=8,-t0 π T为常数,日,为起始相位 80= 2
1.FIR滤波器的定义 传输函数 1 ( ) ( ) () ( ) N j jn j He hne H e 幅度特性(可为负值) 0 ( ) () ( ) g n He hne H e 幅度特性(可为负值) Hg() - 与幅频响应不同 相位特性 Hg() () 与幅频响应不同 - 与相频响应不同 第一类线性相位FIRDR 严格线性函数: () 第二类线性相位FIRDR () ( ) 满足: 为常数 为起始相位 0 ( ) 7 为常数, 0 为起始相位 0 2

系统的群时延 t(o)- dθ(o) do 群时延均为常数,称为恒定群延时滤波器: d0(o) do (θ(o)=-t0,0(o)=0,-t0)
系统的群时延 ( ) ( ) d d 群时延均为常数,称为恒定群延时滤波器 恒定群延时滤波器: d ( ) d (, ) () 0 ( ) 8
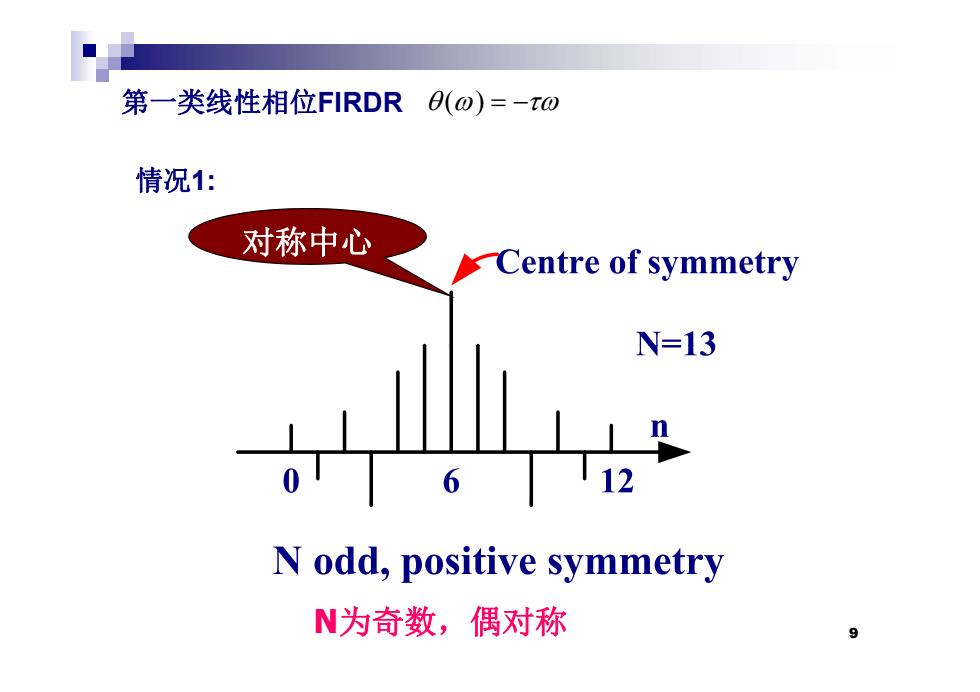
第一类线性相位FIRDR(o)=-tO 情况1: 对称中心 Centre of symmetry N=13 N odd,positive symmetry N为奇数,偶对称
第 类线性相位 一 FIRDR () 情况1: () 情况1: 对称中心 N为奇数,偶对称 9

第一类线性相位FIRDR(o)=-to 情况2: 对称中心 Centre of symmetry N=12 n N even,positive symmetry N为偶数,偶对称 10
第一类线性相位FIRDR () 情况 2: 对称中心 第 类线性相位FIRDR () 情况 2: 对称中心 10 N为偶数,偶对称
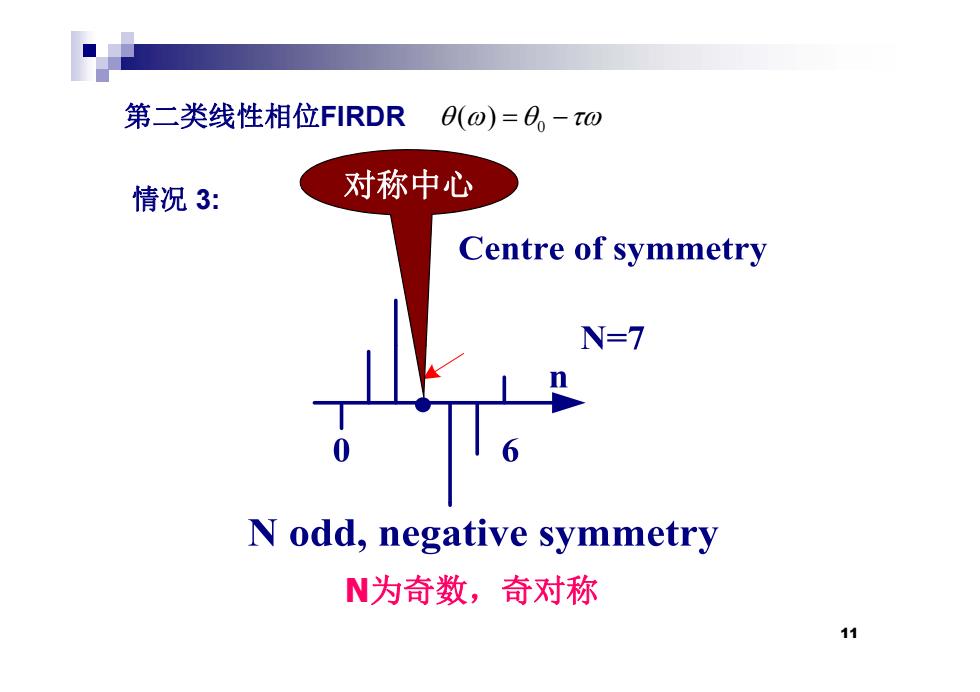
第二类线性相位FIRDR 0(0)=0-t0 情况3: 对称中心 Centre of symmetry N=7 N odd,negative symmetry N为奇数,奇对称 11
第二类线性相位FIRDR ( ) 情况 3 对称中心 第二类线性相位FIRDR 0 ( ) 情况 3: 对称中心 N为奇数 奇对称 11