
第三章 结构地震反应分析与抗震计算 重点掌握内容 ·结构地震反应 ·地震反应谱 ·底部剪力法 ·结构基本周期 本章是全课的重点!!!
1 第三章 结构地震反应分析与抗震计算 重点掌握内容 结构地震反应 地震反应谱 底部剪力法 结构基本周期 本章是全课的重点!!!

第三章 结构地震反应分析与抗震计算 >第一节 概述 >第二节单自由度体系的弹性地震反应分析 > 第三节单自由度体系的水平地震作用与反应谱 >第四节多自由度弹性体系的地震反应分析 > 第五节多自由度弹性体系的最大地震反应与水平地震作 > 第六节竖向地震作用(了解) > 第七节结构平扭耦合地震反应与双向水平地震影响(不 做要求) > 第八节结构非弹性地震反应分析(了解) > 第九节结构抗震验算(了解) > 小结 > 习题
2 第三章 结构地震反应分析与抗震计算 第一节 概述 第二节 单自由度体系的弹性地震反应分析 第三节 单自由度体系的水平地震作用与反应谱 第四节 多自由度弹性体系的地震反应分析 第五节 多自由度弹性体系的最大地震反应与水平地震作 用 第六节 竖向地震作用(了解) 第七节 结构平扭耦合地震反应与双向水平地震影响(不 做要求) 第八节 结构非弹性地震反应分析(了解) 第九节 结构抗震验算(了解) 小 结 习 题

第一节 概述 >1.1结构地震反应 >由地震动引起的结构内力、变形、位移及结构 运动速度与加速度等统称结构地震反应。 ·地震作用:是指地面震动在结构上产生动力荷载 俗称为地震荷载。注意:是间接作用 ·地震作用效应:地震作用产生结构的内力和变形 > 结构动力特性 ◆结构的自振周期、阻尼、振型等。 3
3 第一节 概述 1.1 结构地震反应 由地震动引起的结构内力、变形、位移及结构 运动速度与加速度等统称结构地震反应。 地震作用:是指地面震动在结构上产生动力荷载, 俗称为地震荷载。注意:是间接作用 地震作用效应:地震作用产生结构的内力和变形 结构动力特性 结构的自振周期、阻尼、振型等

进行结构地震反应分析的第一步,就是确定结 构动力计算简图。结构动力计算的关键是结构 惯性的模拟,由于结构的惯性是结构质量引起 的,因此结构动力计算简图的核心内容是结构 质量的描述。描述结构质量的方法有两种, 种是连续化描述(分布质量),另一种是集中化 描述(集中质量)。如采用连续化方法描述结构 的质量,结构的运动方程将为偏微分方程的形 式,而一般情况下偏微分方程的求解和实际应 用不方便。因此,工程上常采用集中化方法描 述结构的质量,以此确定结构动力计算简图
4 进行结构地震反应分析的第一步,就是确定结 构动力计算简图。结构动力计算的关键是结构 惯性的模拟,由于结构的惯性是结构质量引起 的,因此结构动力计算简图的核心内容是结构 质量的描述。描述结构质量的方法有两种,一 种是连续化描述(分布质量),另一种是集中化 描述(集中质量)。如采用连续化方法描述结构 的质量,结构的运动方程将为偏微分方程的形 式,而一般情况下偏微分方程的求解和实际应 用不方便。因此,工程上常采用集中化方法描 述结构的质量,以此确定结构动力计算简图

地震作用的简化: 地震作用简化为三个方向:两个水平方向, 一个竖向。 一般分别计算三个方向的 地震作用
5 地震作用简化为三个方向:两个水平方向, 一个竖向。 地震作用的简化: 一般分别计算三个方向的 地震作用
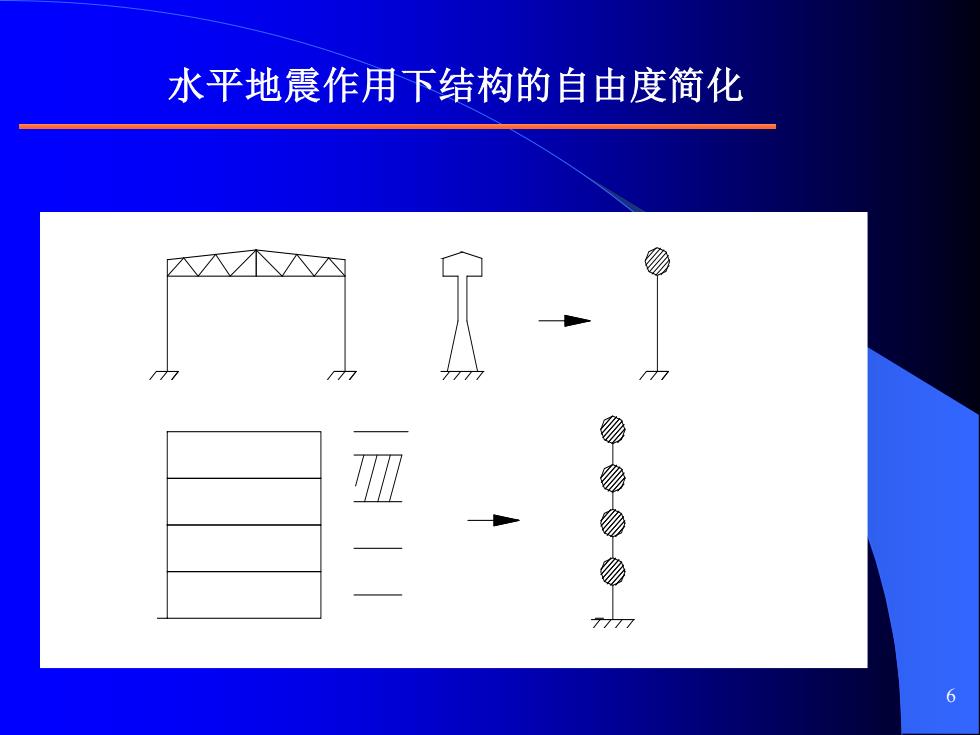
水平地震作用下结构的自由度简化 6
6 水平地震作用下结构的自由度简化

体系的自由度问题 一个自由质点,若不考虑其转动,则相对于 空间坐标系有3个独立的唯一分量,因而有三个 自由度(上下、左右、前后),而在平面内只有 两个自由度 如果忽略直杆的轴向变形,则 在平面内与直杆相连的质点 只有一个位移分量,即只有 个自由度
7 体系的自由度问题 一个自由质点,若不考虑其转动,则相对于 空间坐标系有3个独立的唯一分量,因而有三个 自由度(上下、左右、前后),而在平面内只有 两个自由度. 如果忽略直杆的轴向变形,则 在平面内与直杆相连的质点 只有一个位移分量,即只有一 个自由度
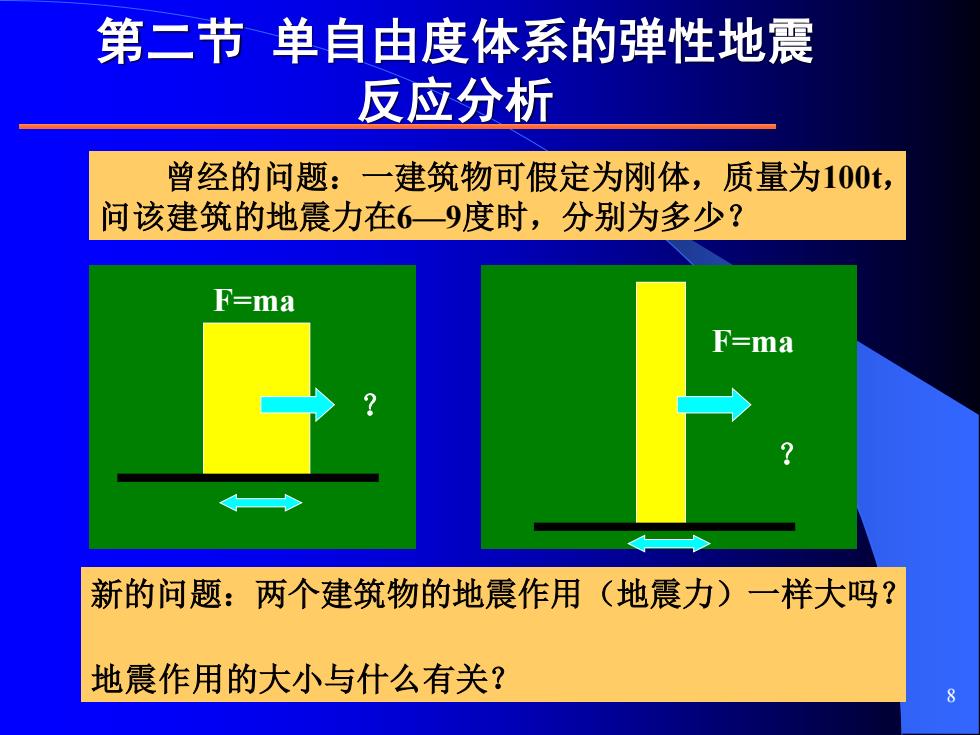
第二节单自由度体系的弹性地震 反应分析 曾经的问题:一建筑物可假定为刚体,质量为100t, 问该建筑的地震力在6一9度时,分别为多少? F=ma F=ma 新的问题:两个建筑物的地震作用(地震力)一样大吗? 地震作用的大小与什么有关? P
8 第二节 单自由度体系的弹性地震 反应分析 ? F=ma 曾经的问题:一建筑物可假定为刚体,质量为100t, 问该建筑的地震力在6—9度时,分别为多少? ? F=ma 新的问题:两个建筑物的地震作用(地震力)一样大吗? 地震作用的大小与什么有关?

2.1单自由度体系的弹性地震反应分析 1、运动方程建立 作用于质量m上的水平方向的为: (1 惯性力f,ma (2) 弹性恢复力fr f,=-k “-”表示与x方向相反 (3 阻尼力fc f。=-cx 是-*ma f. x() 9
9 2.1 单自由度体系的弹性地震反应分析 作用于质量m上的水平方向的力: (1) 惯性力 fI=ma (2) 弹性恢复力 fr (3) 阻尼力 fc fI=ma ( ) g x t x t( ) fc fr m “-”表示与x方向相反 1、运动方程建立 f kx r = − & f cx c = − &

质量m的绝对加速度: a=x+xs >由牛顿第二定律: F=a·m -k-=m(+xg) 单质点的地震作用 只要求解出戈,就求出了质点的地震作用。 10
10 质量m的绝对加速度: 由牛顿第二定律: a x = + xg = − − = + ( ) F a m kx cx m x xg = − − = + ( ) F a m kx cx m x xg 单质点的地震作用 F a m kx cx m x = − − = + 只要求解出( ) ,就求出了质点的 xg 地震作用