
第二章多组分系统热力学
第二章 多组分系统热力学

第二章多组分系统热力学 前一章对象为单组分系统(纯物质)或组成恒定的系 统。 。 常见的系统绝大部分为多组分系统或变组分系统 一些基本概念及名词术语: 多组分单相系统:是由两种或两种以上物质以分子大小 相互均匀混合而成的均匀系统。 混合物:当对均匀系统中各组分(B、C、D)均选用 同样的标准态和同样方法加以研究时,称之为混合物。 溶液:当将均匀系统中的组分区分为溶剂(A)和溶质 (B),而对二者选用不同的标准态和不同的方法加以 研究时,称之为溶液
第二章 多组分系统热力学 • 前一章对象为单组分系统(纯物质)或组成恒定的系 统。 • 常见的系统绝大部分为多组分系统或变组分系统 • 一些基本概念及名词术语: • 多组分单相系统:是由两种或两种以上物质以分子大小 相互均匀混合而成的均匀系统。 • 混合物:当对均匀系统中各组分( B 、 C 、 D)均选用 同样的标准态和同样方法加以研究时,称之为混合物。 • 溶液:当将均匀系统中的组分区分为溶剂( A)和溶质 ( B),而对二者选用不同的标准态和不同的方法加以 研究时,称之为溶液
§2一1偏摩尔量与化学势 1、偏摩尔量 (1)偏摩尔量的定义 乙浓 醇+'水 V醇+水 AV/cm3 Wa% cm' cm >第一,乙醇与 水混合后所得溶 10 12.67 90.36 103.3 101.84 1.19 液体积不等于混 20 25.34 80.32 105.66 103.22 2.42 合前乙醇与水的 38.01 70.28 108.29 104.84 3.45 体积之和; 40 50.68 60.24 110.92 106.93 3.09 >第二,100g溶 液的体积与组成 % 63.35 50.20 113.55 109.43 4.12 有关。 60 76.02 40.16 116.18 112.22 3.96 70 88.69 30.12 118.81 115.25 3.56 80 101.36 20.08 121.44 118.56 2.88 90 114.03 10.04 124.07 122.25 1.82
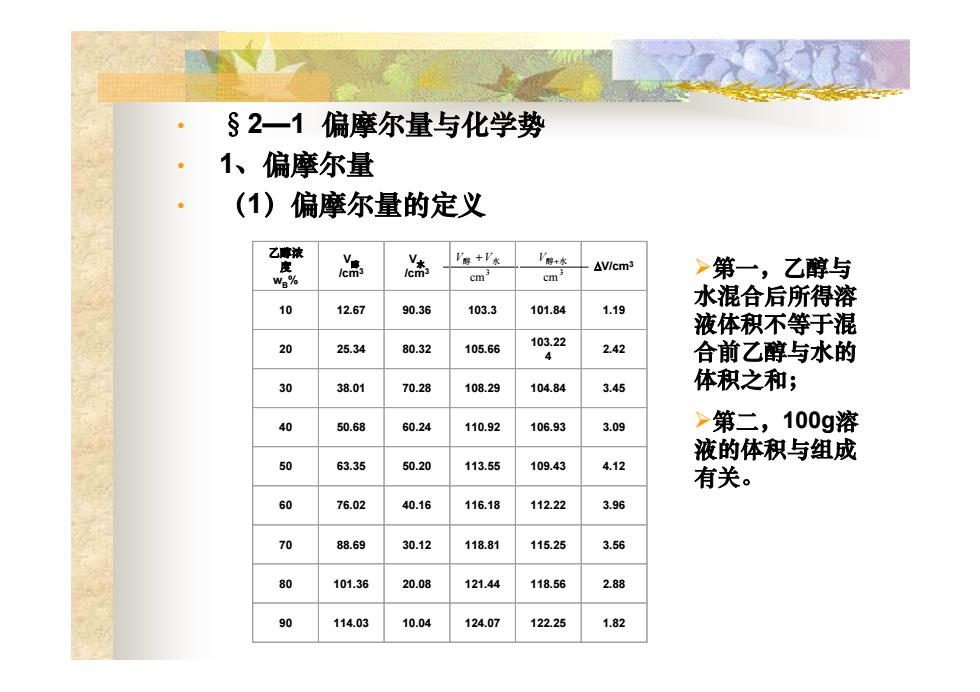
• §2—1 偏摩尔量与化学势 • 1、偏摩尔量 • (1)偏摩尔量的定义 3 cm V醇 + V水 乙醇浓度 wB% V醇 /cm3 V水 /cm3 ΔV/cm3 10 12.67 90.36 103.3 101.84 1.19 20 25.34 80.32 105.66 103.22 4 2.42 30 38.01 70.28 108.29 104.84 3.45 40 50.68 60.24 110.92 106.93 3.09 50 63.35 50.20 113.55 109.43 4.12 60 76.02 40.16 116.18 112.22 3.96 70 88.69 30.12 118.81 115.25 3.56 80 101.36 20.08 121.44 118.56 2.88 90 114.03 10.04 124.07 122.25 1.82 3 cm V醇+水 ¾第一,乙醇与 水混合后所得溶 液体积不等于混 合前乙醇与水的 体积之和; ¾第二,100g溶 液的体积与组成 有关

任一广度性质的状态函数X可表示为 X=X(T,p,nB,ncnD.) dx=( +p+ 式(2-1-2)中偏导数下标nc代表系统的组分ng ncno.均不变。nc≠B表示除B以外的其他组分均 不变。 ax )T,P,c≠B 式(2-1-2)中的偏导数 称为偏摩尔量 (partial molar quantity) 用符号X表示,即 XB=(),Pc
• 任一广度性质的状态函数X可表示为 • X = X(T, p, nB, nC, nD,.) • 式(2-1-2)中偏导数下标nC代表系统的组分nB、 nC、nD.均不变。nC≠B表示除B以外的其他组分均 不变。 • 式(2-1-2)中的偏导数 称为偏摩尔量 (partial molar quantity),用符号XB表示,即 ∑ ≠ ∂∂ + ∂∂ + ∂∂ = B T p n B B p n T n n nX p pX T TX X C C C B d ( ) d ( ) d ( ) d , , , , T p nC B B n X ≠ ∂ ∂ , , ( ) , , ( ) B T pnC B B X X n ≠ ∂ = ∂ ∂ + ∑ ∂ + ∂∂ = B p n T n B B p X n TX T TX X C C d ( ) d ( ) d d ,

XB= ∂ns )T.p.nca 关于偏摩尔量,以下几点值得注意: 第一,只有广度性质的状态函数才有偏摩尔量, 强度性质的状态 函数不存在偏摩尔量; 第二,只有广度性质的状态函数X在温度、压力和除B以外的其 他组分保持不变的条件下,对组分B的物质的量的偏导数才称为 偏摩尔量; 第三,偏摩尔量是强度性质的状态函数,与系统的温度、压力和 组成有关。 多组分均相系统中组分B的一些偏摩尔量如下: VB=( ∂U Hn= UB=( dn )T.p.nc+B T.p.nceB )T.p.nc+B SB= as ∂G ∂ng A8=( )T.p.ncB gR= )T,p.nc+B T,p,ncB
• 关于偏摩尔量,以下几点值得注意: • 第一,只有广度性质的状态函数才有偏摩尔量,强度性质的状态 函数不存在偏摩尔量 ; • 第二,只有广度性质的状态函数X在温度、压力和除B以外的其 他组分保持不变的条件下,对组分B的物质的量的偏导数才称为 偏摩尔量; • 第三,偏摩尔量是强度性质的状态函数,与系统的温度、压力和 组成有关。 • 多组分均相系统中组分B的一些偏摩尔量如下: , , ( ) B T pnC B B V V n ≠ ∂ = ∂ , , ( ) B T pnC B BU U n ≠ ∂ = ∂ , , ( ) B T pnC B BH H n ≠ ∂ = ∂ , , C B B B T pn S S n ≠ ∂ = ∂ , , ( ) B T pnC B BA A n ≠ ∂ = ∂ , , ( ) B T pnC B BG G n ≠ ∂ = ∂ , , ( ) B T pnC B B X X n ≠ ∂ = ∂

(2)偏摩尔量集合公式 B 当温度、压力恒定时,由式(21-4)得 dr-∑X adng R X=∑。X。 上式称为偏摩尔量集合公式,该式表明,在温度、压 力恒定条件下,多组分均相系统的广度性质的状态函 数等于该系统各组分的偏摩尔量与物质的量的乘积之 和
• (2)偏摩尔量集合公式 • 当温度、压力恒定时,由式(2-1-4)得 • 上式称为偏摩尔量集合公式,该式表明,在温度、压 力恒定条件下, 多组分均相系统的广度性质的状态函 数等于该系统各组分的偏摩尔量与物质的量的乘积之 和。 B B B dX = ∑ X dn B B B B B n B X X X X n n X B = ∫0 d = ∑∫0 d = ∑ ∂ + ∑ ∂ + ∂∂ = B p n T n B B p X n TX T TX X C C d ( ) d ( ) d d , , B B B X = ∑n X

(3)吉布斯一杜亥姆公式 当温度、压力恒定时, X=∑nX。 dX-∑X adna+∑ngdX p dX=∑X pdna B ∑n,dXB=0 上式称为吉布斯一杜亥姆(Gibbs-Duhem)公式, 其成立的条件是恒温、恒压。 例如对由溶剂A和溶质B组成的二元溶液来说,吉布 斯一杜亥姆公式为 。 nAdXA nedXB=0 dXa=·(ngna)dXg
• (3)吉布斯—杜亥姆公式 • 当温度、压力恒定时, • 上式称为吉布斯—杜亥姆(Gibbs-Duhem)公式, 其成立的条件是恒温、恒压。 • 例如对由溶剂A和溶质B组成的二元溶液来说,吉布 斯—杜亥姆公式为 • nAdXA + nBdXB = 0 • dXA = -(nB/nA)dXB B B B X = ∑n X B B B B B dX = ∑ X B dn + ∑n dX d 0 B B B ∑n X = B B B dX = ∑ X dn

(4)偏摩尔量之间的函数关系 ·前一章我们讨论的一些热力学关系式只适用于单组分均 相系统,将这些关系对于混合物中任一组分B取偏导 数,可知各偏导数之间也有着同样的关系,即 ·He=Ue+pVB ·Ag=UBTSB 。 Ge=HB-TSB )V p
• (4)偏摩尔量之间的函数关系 • 前一章我们讨论的一些热力学关系式只适用于单组分均 相系统,将这些关系对于混合物中任一组分B取偏导 数,可知各偏导数之间也有着同样的关系,即 • HB = UB + pVB • AB =UB - TSB • GB =HB - TSB , ( ) C B Tn B G V p ∂ = ∂ , () C B p n B G S T ∂ = − ∂

2、化学势 (1)化学势的定义 在多组分均相系统中,组分B的偏摩尔吉布斯函数又 称为化学势(chemical potential)),并用符号e表 示,即 ∂G UB=GR= .p.nc+B G=G(T,p,ng,nc,np.) ap 9m=-S dG=-SdT+Vdp+∑4sdne
• 2、化学势 • (1)化学势的定义 • 在多组分均相系统中,组分B的偏摩尔吉布斯函数又 称为化学势(chemical potential),并用符号μB表 示,即 • G = G(T, p, nB, nC, nD,.) , , ( ) B B T pnC B B G G n µ ≠ ∂ = = ∂ T p n B B B p n T n n n G p p G T T G G C C C B d ( ) d ( ) d ( ) d , , , , ≠ ∂∂ + ∂∂ + ∂∂ = ∑ ( ) ( ) , , S TG V pG T nC p nC = − ∂∂ = ∂∂ dB B B dG SdT Vdp n =− + +∑µ

由热力学基本关系式得: dU=S-pd+】4 B d-+Hr∑4 d4-sr-d+∑4dh U=U(S,V,ng,nc,np,.) H=H(S,p,ng,nc,no.) +峰票n4 A=A(T,V,ng,nc,nb.) UB= )T.p.nceB -5,cB dn. S:p.nceB
• 由热力学基本关系式得: • U = U(S, V, nB, nC, nD,.) • H = H(S, p, nB, nC, nD,.) • A = A(T, V, nB, nC, nD,.) dB B B dU TdS pdV n =− +∑µ dB B B dH TdS Vdp n =++∑µ dB B B dA SdT pdV n =− − +∑µ , , () d C B SVn B B B U dU TdS pdV n n ≠ ∂ =− + ∂ ∑ , , () d C B S pn B B B H dH TdS Vdp n n ≠ ∂ =++ ∂ ∑ , , () d TVn B C B B A A dA SdT pdV n n ≠ ∂ =− − + ∂ ∑ C B C B C B T V nC B B S p n B S V n B T p n B B n A n H n U n G ≠ ≠ ≠ ≠ ∂ ∂ = ∂ ∂ = ∂ ∂ = ∂ ∂ = , , , , , , , , µ ( ) ( ) ( ) ( )